Дійсне число також визначається як нескінченна десяткова дріб, і тоді вираз виду. де є один із символів або. званий знаком числа, - ціле невід'ємне число, - послідовність десяткових знаків, тобто елементів числового безлічі.
Нескінченна десяткова дріб інтерпретується як таке число, яке на числовій прямій лежить між раціональними точками виду
Порівняння дійсних чисел у формі нескінченних десяткових дробів проводиться поразрядно. Наприклад, нехай дано два невід'ємних числа
Якщо. то; якщо то. У разі рівного розподілу переходять до порівняння наступного розряду. І так далі. Якщо. то після кінцевого числа кроків зустрінеться перший розряд. такий що. Якщо. то; якщо то .
Однак, при порівнянні нескінченних десяткових дробів необхідно враховувати, що число. У такому випадку, якщо запис одного з чисел, які ми порівнюємо, починаючи з деякого розряду, являє собою періодичну десяткову дріб, у якої в періоді коштує 9, то її слід замінити на еквівалентну запис, з нулем в періоді.
Арифметичні операції над нескінченними десятковими дробами визначаються як безперервне продовження [14] відповідних операцій над раціональними числами. Наприклад, сумою дійсних чисел і називається дійсне число. задовольняє наступній умові:
Аналогічним способом визначається операція множення на безлічі нескінченних десяткових дробів.
У більшості випадків точне приватне у вигляді десяткового дробу не може бути отримано, як би далеко не тривало розподіл.
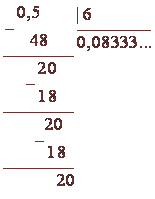
Дріб перетворюється в чисту періодичну десяткову, так як 27 не ділиться ні на 2, ні на 5. Дріб перетворюється в змішану періодичну, так як 12 ділиться на 2.
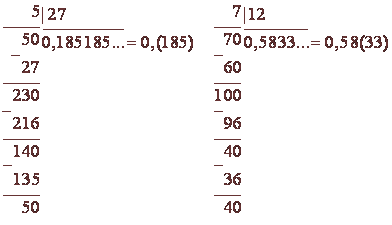
Доведіть, що нескінченна десяткова дріб +0,1234567891011121314. (Після коми поспіль виписані всі натуральні числа по порядку) являє собою ірраціональне число.
Як відомо, раціональні числа виражаються десятковими дробами, які мають період починаючи з деякого знака. Виходячи з цього, досить довести, що дана дріб не є періодичною ні з якого знака. Покладемо, що це не так, і деяка послідовність T, що складається з n цифр, є періодом дробу, починаючи з m-го знака після коми. В такому випадку, що серед цифр після m-го знака зустрічаються ненульові, тому в послідовності цифр T є ненульова цифра. Це означає, що починаючи з m-ой цифри після коми, серед будь-яких n цифр поспіль є ненульова цифра. Але в десяткового запису даної дробу має бути присутня десяткова запис числа 100. 0 = 10 k. де k> m і k> n. Зрозуміло, що цей запис зустрінеться правіше m-ой цифри і містить більш n нулів підряд. Таким чином, ми маємо протиріччя, яким завершує доказ.
Дана нескінченна десяткова дріб 0, a1 a2. Доведіть, що цифри в її десяткового запису можна переставити так, щоб отримана дріб висловлювала раціональне число.
Дріб висловлює раціональне число в тому і тільки тому випадку, коли вона періодична, починаючи з деякого знака. Цифри від 0 до 9 розділимо на два класи: до першого класу включимо ті цифри, які зустрічаються у вихідній дробу кінцеве число раз, до другого класу - ті, які зустрічаються у вихідній дробу нескінченну кількість разів. Почнемо виписувати періодичну дріб, яка може бути отримана з вихідної перестановкою цифр. Спочатку після нуля і коми напишемо в довільному порядку всі цифри з першого класу - кожну стільки раз, скільки вона зустрічається в запису вихідної дробу. Записані цифри першого класу будуть передувати періоду в дробової частини десяткового дробу. Далі, запишемо в деякому порядку по одному разу цифри з другого класу. Отриману комбінацію назвемо періодом і будемо повторювати її нескінченне число разів. Таким способом, ми виписали шукану періодичну дріб, яка має деяке раціональне число.
Довести, що в кожної нескінченного десяткового дробу існує послідовність десяткових знаків довільної довжини, яка в розкладанні дробу зустрічається нескінченно багато разів.
Нехай m - довільно задане натуральне число. Розіб'ємо цю нескінченну десяткову дріб на відрізки, по m чисел в кожному. Таких відрізків буде нескінченно багато. З іншого боку, різних систем, що складаються з m чисел, існує тільки 10 m. т. е. кінцеве число. Отже, хоча б одна з цих систем повинна повторюватися тут нескінченно багато разів.
Зауваження. Для ірраціональних чисел # 118; 2, р або е ми навіть не знаємо, яка цифра повторюється нескінченно багато разів в відповідних їм нескінченних десяткових дробах, хоча кожне з цих чисел, як легко можна довести, містить принаймні дві різні такі цифри.
Перевірте розподілом стовпчиком, що
Таким чином, всі раціональні числа містяться серед нескінченних десяткових дробів як періодичні десяткові дроби.
Дійсними числами називають нескінченні десяткові дроби зі знаком плюс або мінус, і в разі періодичності дробу таке дійсне число називають раціональними, в іншому випадку - ірраціональним.
Число а = 0.1010010001. як неперіодичних нескінченна десяткова дріб є число ірраціональне.
Порівняно просто визначати в відношення рівності і порядку ( "більше") Нехай a = 0. 1. 2. b = 0. 1. 2
дійсні числа. Будемо вважати їх рівними, якщо вони одного знака і k = 0, 1, 2. k = k.
Нехай a, b одного знака "+". Число a більше числа b (a b), якщо існує k = 0, 1, 2. що i = i для i = 1, 2. k - 1 і kk