Правило множення матриць
Нехай дано 2 матриці A (m × n) і B (n × l), причому число стовпців матриці A дорівнює числу рядків матриці B. Тоді матриця C (m × l) з елементами. (Тобто i-тая рядок матриці A, помножена скалярно на j-й стовпець матриці B, дає cij -й елемент матриці C, що стоїть в i-му рядку і j-му стовпці).
. .
Властивість системи лінійних рівнянь, що містить тривіальне рівняння.
Тривіальне рівняння - рівняння, в якому коефіцієнти при всіх невідомих і вільних членах дорівнюють нулю.
Теорема: Система лінійних рівнянь, що містить тривіальне рівняння, рівносильна тій же системі без тривіального рівняння.
Доказ: Розглянемо слу (1) і ту ж слу (2), але без тривіального рівняння.
Нехай вектор є рішенням системи (1), тоді цей вектор є і рішенням системи (2).
Назад, нехай вектор є рішенням системи (2). Оскільки n-мірний вектор L є і рішенням тривіального рівняння, то він є рішенням системи (1).
Таким чином, система лінійних рівнянь, що містить тривіальне рівняння, рівносильна цій же системі без тривіального рівняння.
Властивість вільних невідомих в дозволеної слу
Слу називається дозволеної. якщо кожне рівняння системи містить хоча б один використаний невідоме.
Теорема: Якщо в дозволеної слу (4) надати вільним невідомим довільні значення. т. е.. то знайдеться єдине рішення цієї системи у вигляді n-мірного вектора К, у якого значення координат, відповідних вільним невідомим, рівні відповідно.
Підставами в систему (4). Тоді дозволені невідомі приймуть значення такі, що:
Т. к. Вектор звертає кожне рівняння системи (4) в точне числове рівність, то він є рішенням цієї системи. Таким чином, доведено існування рішення системи (4).
Доведемо єдиність такого рішення. Нехай вектор з тими ж значеннями вільних невідомих є також рішенням системи (4). Тоді підставимо його в систему (4), отримаємо:
Зіставляючи (5) і (6), бачимо, що. Таким чином, доведено, що існує єдине рішення системи (4) з заданими значеннями вільних невідомих.
1) Т. к. Значення вільних невідомих можна задати нескінченно великим числом способів, то система (4) є невизначеною.
2) Дозволена слу завжди сумісна. При цьому вона визначена. якщо m = n. т. е. число рівнянь дорівнює числу невідомих, і не визначена. якщо число рівнянь менше числа невідомих, т. е. m Рішення системи однорідних рівнянь Лінійне рівняння називається однорідним. якщо його вільний член дорівнює нулю, і неоднорідним в іншому випадку. Система, що складається з однорідних рівнянь, називається однорідним і має загальний вигляд: 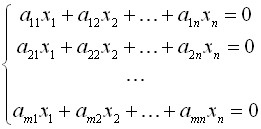
Теорема. Однорідна система лінійних рівнянь має ненульовий розв'язок тоді і тільки тоді, коли її ранг менше числа невідомих.
Доказ: Припустимо, система, ранг якої дорівнює. має нульове рішення. Очевидно, що не перевищує. У разі система має єдине рішення. Оскільки система однорідних лінійних рівнянь завжди має нульове рішення, то саме нульове рішення і буде цим єдиним рішенням. Таким чином, ненульові рішення можливі тільки при.
Слідство 1: Однорідна система рівнянь, в якій число рівнянь менше числа невідомих, завжди має нульове рішення.
Доказ: Якщо у системи рівнянь. то ранг системи не перевищує числа рівнянь. тобто . Таким чином, виконується умова і, отже, система має ненульовий розв'язок.
Слідство 2: Однорідна система рівнянь з невідомими має ненульовий розв'язок тоді і тільки тоді, коли її визначник дорівнює нулю.
Доказ: Припустимо, система лінійних однорідних рівнянь, матриця якої з визначником. має нульове рішення. Тоді по доведеною теоремою. а це значить, що матриця вироджена, тобто .
Приклади лінійно залежних і лінійно незалежних систем векторів
1) Система m -мірних векторів називається лінійно залежною. якщо система лінійних рівнянь (1) має ненульові рішення. Якщо ж система (1) не має ненульових рішень, то дана система векторів є лінійно незалежною.
2) Система m -мірних векторів називається лінійно залежною. якщо існує такий ненульовий вектор. що виконується лінійне співвідношення (2). Якщо ж з будь-якого співвідношення виду (2) випливає, що. то система векторів називається лінійно незалежною.
Приклади завдань лінійного програмування: випуск продукції, раціон, транспортна, портфель цінних паперів.