Розглянемо основний геометричний сенс подвійного інтеграла. Припускаємо, що функція існує в кожній точці плоскої області.
Геометрично функція двох змінних задає деяку поверхню в тривимірному просторі. Для визначеності вважаємо, що. тобто поверхня розташовується над площиною.
Тоді подвійний інтеграл чисельно дорівнює обсягу циліндричного бруса:
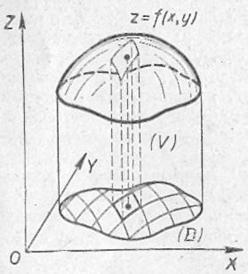
Що таке циліндричний брус, думаю, всім зрозуміло з креслення. Плоска фігура (заштрихована на кресленні) повністю лежить в площині і брус обмежений областю знизу. Зверху брус якраз обмежений поверхнею. яка являє собою таку шапку. Образно кажучи, плоска область по своєму кордоні перпендикулярними променями вирізає з поверхні цю шапочку.
Додатково поясню геометричний сенс на Примері 1. У ньому ми розглядали подвійний інтеграл. причому область інтегрування мала такий вигляд:
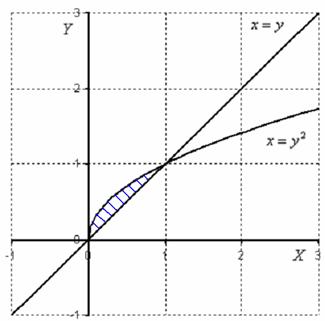
Підінтегральна функція задає площину в просторі. З початку координат перпендикулярно екрану монітора подумки проведіть на себе стрілку осі. В даному прикладі площину розташовується в просторі над областю. тому обсяг тіла вийшов позитивним:. Можливо, не всім до кінця зрозуміло, про який обсяг йде мова: з кордону області направте на себе промені. Ці промені виріжуть шматочок з площини. яка лежить над областю.
Подвійний інтеграл може бути і негативним, в таких випадках графік функції повністю (або більшою частиною) лежить під областю. Це теж обсяг тіла, тільки зі знаком мінус, оскільки поверхня повністю (або більшою частиною) лежить під координатної площиною.
Прошу вибачення, поки не підшукав програми для побудови тривимірних креслень, яка б мене влаштовувала, довелося пояснювати на пальцях.
Однак на практиці майже завжди зустрічаються завдання на формальне обчислення подвійних інтегралів, тому ми продовжимо вдосконалювати техніку обчислень:
Обчислити подвійний інтеграл
.
Рішення: Зобразимо область інтегрування на кресленні:
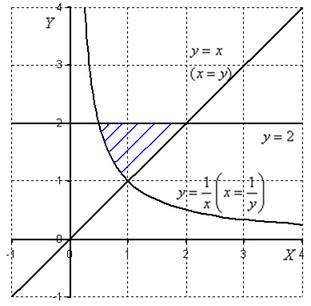
Після того, як коректно виконаний креслення і правильно знайдена область інтегрування, саме час розібратися з порядком обходу.
Відповідно до першого способу обходу, область доведеться розділити на дві частини, при цьому необхідно буде обчислити наступні інтеграли:
Ентузіазму, прямо скажемо, мало. Проаналізуємо, а чи не простіше використовувати другий спосіб обходу області? Перейдемо до зворотних функцій, перехід тут проста:
Порядок обходу області:
Ну ось, зовсім інша справа. І знову зауважте, що у внутрішньому інтегралі інтегрування здійснюється по «ікс», тому константу можна відразу винести в зовнішній інтеграл
1) Знайдемо внутрішній інтеграл:
Все-таки підстановка меж інтегрування, часом, виглядає своєрідно. Сначалавместо «ікси» ми підставили верхня межа інтегрування. потім замість «ікси» підставили нижня межа інтегрування. Будьте уважні при підстановках!
2) Результат попереднього пункту підставимо у зовнішній інтеграл, при цьому не забуваємо про. який там вже знаходиться:
Для тренування можете спробувати обчислити подвійний інтеграл менш раціональним способом:. Результати повинні співпасти.
Обчислити подвійний інтеграл
.
Це приклад для самостійного рішення. Побудуйте область і проаналізуйте, який спосіб обходу області вигідніше використовувати. Повне рішення і відповідь в кінці уроку.
Ускладнюємо завдання, тепер подинтегральная функція буде являти собою суму. Розглянемо ще два приклади, де я зупинюся на прийомі обчислення інтеграла, який типовий і ефективний для кратних інтегралів:
Обчислити подвійний інтеграл
.
Рішення: Спочатку розглянемо те, чого робити не потрібно - в даному випадку не слід використовувати властивості лінійності кратного інтеграла і представляти його у вигляді:
Чому? Обчислень помітно додасться!
Рішення, як зазвичай, починаємо з побудови області інтегрування:
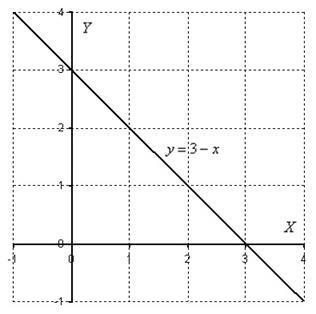
Область нехитра, навіть Штрихована не буду. В даному прикладі, як легко помітити, не має особливого значення порядок інтегрування, тому виберемо перший, більш звичний варіант обходу області:
Тут, на відміну від двох попередніх прикладів, з внутрішнього інтеграла нічого винести не можна, оскільки начинкою є сума.
З повторними інтегралами знову розбираємося окремо. Так, до речі, хто хоче подивитися, як вирішувати повторні інтеграли одним рядком, будь ласка, зайдіть на сторінку Готові рішення з вищої математики та закачайте архів з прикладами рішень кратних інтегралів.
1) Спочатку беремо внутрішній інтеграл:
Хотілося б зупинитися на кількох суттєвих моментах. По-перше, про приватному інтегруванні. Про нього я вже докладно розповідав в статті Диференціальні рівняння в повних диференціалах. Коротенько повторюся: