Рішення практичних завдань по формуванню складних технічних контурів наштовхується на таку проблему, як неможливість подання всього контуру єдиною кривої. Це і породило необхідність конструювання складових кривих (кривих, сформованих з дуг простих).
У техніці такі криві отримали назву обводів, в математиці вони більш відомі як сплайни (spline). Основною характеристикою обвода є гладкість. Під гладкістю розуміють число збіглися похідних (рівнянь стикуються кривих) в точках стику.
Найбільш простий варіант побудови складеної кривої - з дуг кіл.
Кола можуть сполучатися таким чином, що в точках стику будуть розташовуватися загальні дотичні. Такий стик відповідає першому порядку гладкості (збігаються тільки перші похідні).
Для побудови цього обводу використовується ідея радіусі-графічного сполучення дуг кіл. Вихідною інформацією є точковий ряд (1, 2, 3, ..., n) і дотична на одному з кінців цього ряду, наприклад, t i (рисунок 1).
Внаслідок того, що коло трипараметричної крива, для її побудови крім точки i потрібно визначити ще одну, наприклад (i + 1) або (i-1). Не порушуючи спільності міркувань, розглянемо варіант з (i + 1) -ої точкою (рисунок нижче).
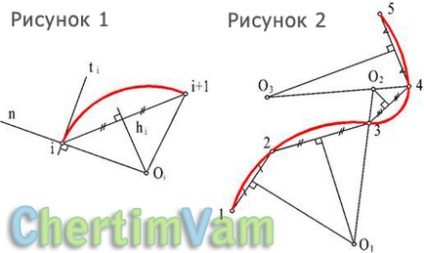
Малюнок 1 - Побудова дуги кола з заданими параметрами
Малюнок 2 - Побудова обвода першого порядку гладкості
Графічне рішення виглядає наступним чином: через точку i проводиться нормаль n. Кінцеві точки i і (i + 1) з'єднуються хордою. У середній точці хорди будується перпендикуляр h. Перетин нормалі n і перпендикуляра h і визначить положення центра шуканої окружності. Радіус кола збігається з відрізками [o-i] і [o- (i + 1)]. Дотична до побудованої окружності буде перпендикулярна радіусу, проведеному в (i + 1) -ю точку.
Центри дотичних кіл лежать на одній прямій, що проходить через точку дотику. Таким чином, визначення центру кола сопрягающейся з i-тій знайдеться на перетині лінії Про i (i + 1) з перпендикуляром до середини хорди (i + 1) (i + 2) (рисунок 2).
побудова кривих
Нижче наведено побудову найбільш найбільш уживаних кривих. На зображенні приведена крива і збережені всі побудови. Нижче описаний алгоритм побудови кривої.
лекальні криві
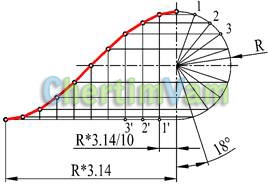
Малюнок 3 - Побудова синусоїди
Синусоїдою називається плоска крива, графічно зображує зміна синуса залежно від його аргументу (кута). Для побудови синусоїди коло радіуса R ділять на довільну кількість рівних частин. На горизонтальній прямій відкладають відрізок, рівний половині довжини кола (R * 3.14), і ділять його на таке ж число рівних частин. З кінців цих відрізків (точки 1 ', 2', 3 ') проводять вертикальні прямі до перетину з горизонтальними прямими, що виходять із-решт відповідних радіусів (точки 1,2,3).
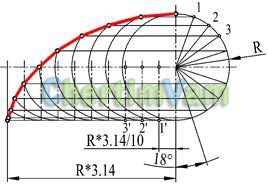
Малюнок 4 - Побудова циклоїди
Циклоїдою називається крива, утворена точкою кола, що котиться без ковзання по прямій лінії. Для побудови циклоїди коло радіуса R ділять на довільну кількість рівних частин. На горизонтальній прямій відкладають відрізок, рівний половині довжини кола (R * 3.14), і ділять його на таке ж число рівних частин. З кінців цих відрізків (точки 1 ', 2', 3 ') проводять вертикальні прямі до перетину з горизонтальною осьової лінією. Ці точки будуть центрами кіл радіуса R. Перетин кіл з відповідними горизонтальними прямими, що виходять із-решт радіусів (точки 1,2,3), дадуть точки циклоїди.
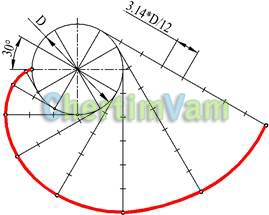
Малюнок 5 - Побудова евольвенти
Евольвентою кола називається крива, яку описує точка прямої лінії, що котиться без ковзання по нерухомій окружності. Окружність діаметра D ділять на довільне число рівних частин. З точок розподілу проводять дотичні до кола, на яких відкладають відповідно 1, 2, 3 і т.д. частини кола.
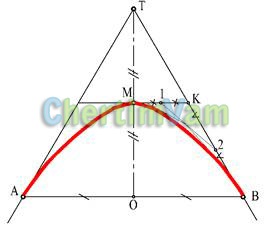
Малюнок 6 - Побудова параболи
Параболойназивается, крива, отримана при перетині конуса і площини, паралельної утворює конуса. При завданні параболи граничними точками А і В і точкою перетину дотичних Т крива будується методом пропорційного розподілу.
Відрізок АВ ділиться навпіл в точці О, відрізок ВІД - теж навпіл в точці М, відрізок МК - в точці 1, КВ - в точці 2 і т.д.
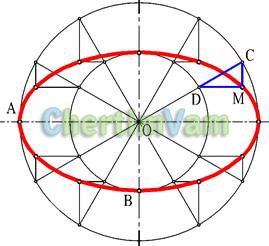
Малюнок 7 - Побудова еліпса
Елліпсомназивается крива, отримана при перетині конуса і площини, що перетинає все утворить конуса.
Еліпс зручніше коштувати по його полуосям (великий ОА і малої ОВ).
Для побудови еліпса проводяться дві співвісні окружності радіусами ОВ і ОА Проведення довільної прямої ОС і подальше побудова "ключа" (трикутника СDМ зі сторонами паралельними осях еліпса) дозволяє визначити положення поточної точки еліпса М.
геометричні побудови
Нижче дані зображення найбільш поширених видів геометричних побудов і описаний алгоритм побудови.
Дотична до еліпсу
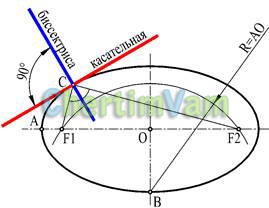
Малюнок 8 - Дотична до еліпсу
Побудова дотичної до еліпса (з півосями ОА і ОВ) в заданій точці С потрібно починати з побудови фокусів еліпса, точок F1 і F2.
Побудувати коло з центром в точці В і радіусом, рівним велика піввісь ОА. У перетині кола з горизонтальною віссю відзначити точки F1 і F2. Побудувати бісектрису кута F1СF2. Пряма, перпендикулярна бісектрисі і проходить через точку С, буде дотичній до еліпса в заданій точці.
Побудова бісектриси кута
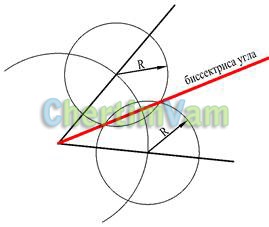
Малюнок 9 - Побудова бісектриси кута
З вершини кута довільним радіусом побудувати дугу окружності. З точок перетину дуги окружності зі сторонами кута побудувати рівні окружності довільного радіуса R. Пряма, що проходить через вершину кута і точки перетину кіл, - бісектриса кута.
Геометричне побудови сполучення прямих
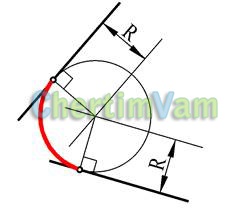
Малюнок 10 - Сполучення прямих окружністю заданого радіуса R
На відстані R від заданих прямих побудувати допоміжні прямі, їм паралельні. З точки перетину допоміжних прямих побудувати сопрягающую окружність заданого радіуса R. Відзначити точки сполучення. Вони лежать на перпендикулярах, проведених з центру сопрягающей окружності до заданим прямим.
Побудова сполучення прямої і дуги
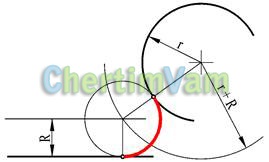
Малюнок 11 - Сполучення окружністю заданого радіуса R прямий і дуги
На відстані R від заданої прямої побудувати допоміжну пряму, їй паралельну. З центру сполучається дуги провести дугу кола з радіусом r + R. З точки перетину побудованої дуги і допоміжної прямої побудувати сопрягающую окружність. Відзначити точки сполучення.
Побудова сполучення двох кіл
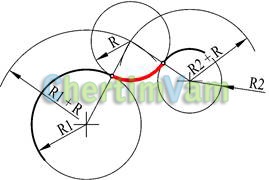
Малюнок 12 - Зовнішнє сполучення окружністю з заданим радіусом R двох кіл з радіусами R1 і R2
З центрів заданих кіл провести дуги допоміжних кіл з радіусами R1 + R і R2 + R. З точки перетину дуг допоміжних кіл побудувати сопрягающую коло радіуса R. Відзначити точки сполучення. Вони лежать на прямих, що з'єднують центри кіл.
Геометричні побудови змішаного сполучення
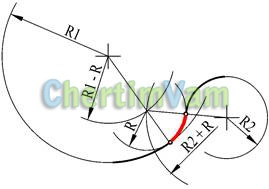
Малюнок 13 - Змішане сполучення окружністю з заданим радіусом R двох кіл з радіусами R1 і R2
З центрів заданих кіл провести дуги допоміжних кіл з радіусами R1-R і R2 + R. З точки перетину дуг допоміжних кіл побудувати сопрягающую коло радіуса R. Відзначити точки сполучення. Вони лежать на прямих, що з'єднують центри кіл.