
Головна | Про нас | Зворотній зв'язок
За визначенням щільність нормально розподіленої випадкової величини дорівнює
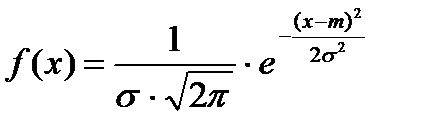
Можливі значення такої величини Х можуть приймати будь-які дійсні значення -∞<Х<∞, а распределение зависит от двух параметров. -∞ Таким чином, графік функції f (х) буде таким: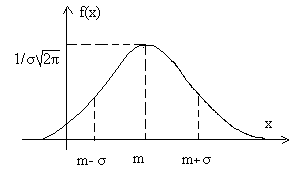
Якщо m = 0 і # 963; = 1. то закон нормального розподілу називається стандартним. В цьому випадку
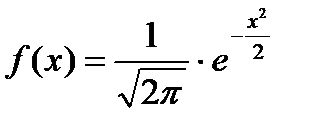
Якщо випадкова величина Х розподілена за нормальним законом з параметрами m і # 963 ;. то цей факт записують так.
Обчислимо математичне сподівання випадкової величини
Таким чином, параметр m - це математичне сподівання випадкової величини X.
Обчислимо тепер дисперсію
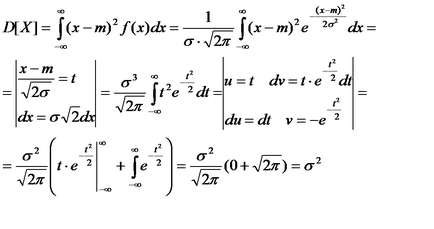
де ми використовували те, що за правилом Лопіталя
Таким чином, параметр # 963; - це середньоквадратичне відхилення, оскільки # 963; 2 - це дисперсія.
Мода і медіана нормального розподілу збігається з математичним очікуванням, тому що максимум f (x) досягається при x = m і
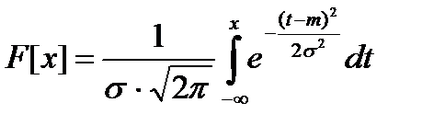
функція розподілу закону яка має графік, представлений на малюнку.
Нехай Обчислимо Р (а<Х де ми використовували формулу Ньютона-Лейбніца для певних інтегралів, а - будь-яка первісна для підінтегральної функції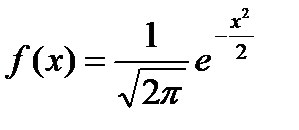
Будь-яка первісна може бути розрахована за формулою
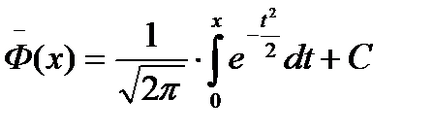
де С - довільна стала. Це можна легко перевірити диффе-ренцірованіем.
При С = 0 ми отримуємо функцію Лапласа
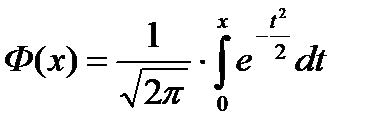
а при С = ∞ - функцію розподілу стандартного нормального закону
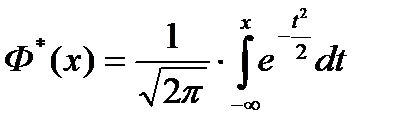
Залежно від наявних у нас під руками таблиць ми скористаємося тієї чи іншої формулою. Відзначимо, що користуватися таблицями функції Лапласа зручніше, так як вона непарна і ми легко - знаходимо її значення при негативному аргументі (зазвичай, таблиці задані тільки для позитивних значень аргументу). Користуватися таблицями функції Ф * (х) в цьому випадку кілька незручно, якщо вона задана тільки для позитивних значень аргументу.
ПРИКЛАД 1. Нехай Знайдемо ймовірність того, що Х прийме значення з інтервалу] 0; 3 [.
По таблиці функції Лапласа отримуємо
По таблиці функції розподілу стандартного нормального закону отримуємо, використовуючи її зв'язок з функцією Лапласа:
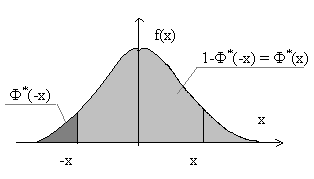
яку легко пояс-нитка наступним малюнком.
Знайдемо ймовірність попадання нормальної випадкової величини в інтервал] m-l, m + l [, симетричний щодо математичного очікування:
При різних l отримуємо
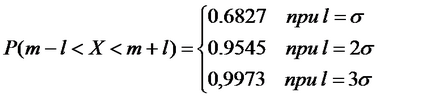
Як ми бачимо, хоча теоретично можливі значення Х можуть бути будь-які, але практично всі значення потрапляють в інтервал] m-3 # 963;, m + 3 # 963; [. Цей факт зазвичай називають правилом «трьох сигм». При нормальному розподілі з 10000 вимірювань тільки 27 мають «законне» право вийти з цього інтервалу (подія малоймовірне і їм зазвичай нехтують). Тому можна вважати, що все віз-можна значення нормальної випадкової величини знаходяться в цьому інтервалі.