а) Комплексні числа зображують точками площини за таким правилом: a + bi = M (a; b) (рис.1).
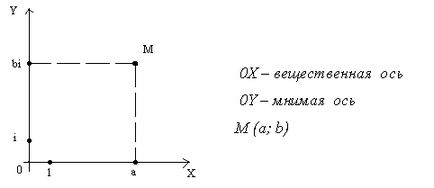
б) Комплексне число можна зобразити вектором, який має початок в точці О і кінець в даній точці (рис.2).
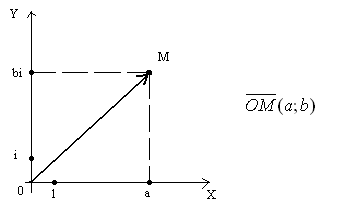
Приклад 7. Побудуйте точки, що зображують комплексні числа: 1; - i; - 1 + i; 2 - 3i (рис.3).
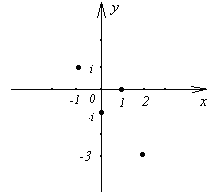
Тригонометрична запис комплексних чисел.
Комплексне число z = a + bi можна задати за допомогою радіус - вектора з координатами (a; b) (рис.4).
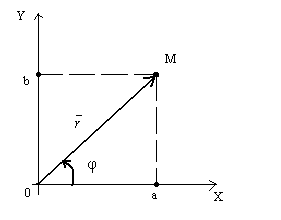
Визначення. Довжина вектора. зображує комплексне число z. називається модулем цього числа і позначається або r.
Для будь-якого комплексного числа z його модуль r = | z | визначається однозначно за формулою.
Визначення. Величина кута між позитивним напрямом дійсної осі і вектором. зображує комплексне число, називається аргументом цього комплексного числа і позначається Аrg z або # 966; .
Аргумент комплексного числа z = 0 не визначено. Аргумент комплексного числа z ≠ 0 - величина багатозначна і визначається з точністю до доданка 2πк (к = 0; - 1; 1; - 2; 2; ...): Arg z = arg z + 2πк. де arg z - головне значення аргументу, укладену в проміжку (-π; π]. тобто -π a = r · cos # 966 ;, b = r · sin # 966; . Отже, комплексне число z = a + bi можна записати у вигляді: z = r · cos # 966; + I r · sin # 966; або z = r · (cos # 966; + I sin # 966;). Такий запис комплексного числа називається тригонометричної формою комплексного числа. Приклад 8. Уявити в тригонометричної формі комплексне число 1 i.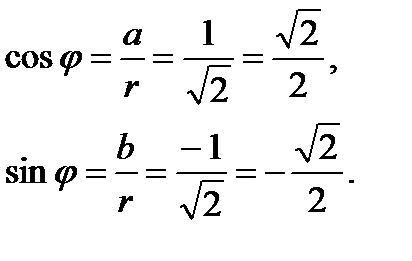
1 - i = (cos + i sin).