Геометричне зображення комплексних чисел 1

Існують такі форми комплексних чисел: алгебраїчна (x + iy), тригонометрическая (r (cos

+isin)), Показова (re i ).

Будь-яке комплексне число z = x + iy можна зобразити на площині ХОУ у вигляді точки А (х, у).

Площина, на якій зображуються комплексні числа, називається площиною комплексного змінного z (на площині ставимо символ z).

Вісь ОХ - дійсна вісь, тобто на ній лежать дійсні числа. ОУ - уявна вісь з уявними числами.

x + iy - алгебраїчна форма запису комплексного числа.

Виведемо тригонометричну форму запису комплексного числа.

;

Підставляємо отримані значення в початкову форму:, тобто

r (cos

+isin) - тригонометрическая форма запису комплексного числа.

Показова форма запису комплексного числа випливає з формули Ейлера:, тоді

z = rei

- показова форма запису комплексного числа.

Дії над комплексними числами.

3. множення. z1 z2 = (x1 + iy1) * (x2 + iy2) = x1x2 + i (x1y2 + x2y1 + iy1y2) = (x1x2-y1y2) + i (x1y2 + x2y1);

4. розподіл. z1 / z2 = (x1 + iy1) / (x2 + iy2) = [(x1 + iy1) * (x2-iy2)] / [(x2 + iy2) * (x2-iy2)] =

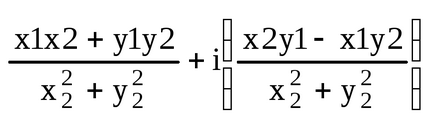
Два комплексних числа, які відрізняються тільки знаком уявної одиниці, тобто z = x + iy (z = x-iy), називаються сполученими.

- Якщо комплексні числа задані в тригонометричної формі.

Те твір z1 * z2 комплексних чисел знаходиться:, тобто модуль добутку дорівнює добутку модулів, а аргумент твори дорівнює сумі аргументів співмножників.

- Якщо комплексні числа задані в показовою формі.

; ;

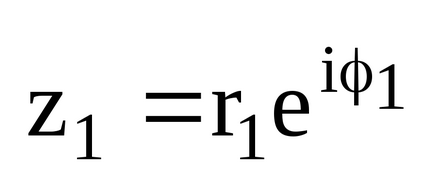
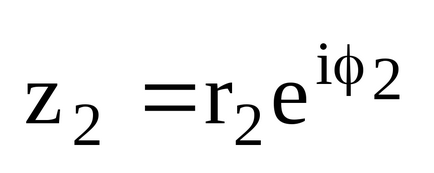
- Якщо комплексні числа задані в тригонометричної формі.

- Якщо комплексні числа задані в показовою формі.

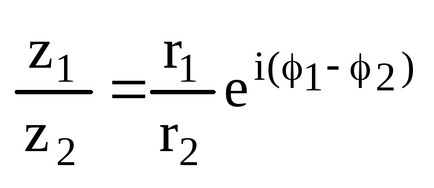
Зведення в ступінь.

1. Комплексне число задано в алгебраїчній формі.

z = x + iy, то z n знаходимо по формулі бінома Ньютона:

- число поєднань з n елементів по m (число способів, скількома можна взяти n елементів з m).

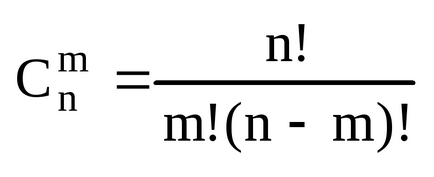
Застосовуємо для комплексного числа.

В отриманому виразі потрібно замінити ступеня i їх значеннями:

i 0 = 1 Звідси, в загальному випадку отримуємо: i 4k = 1

i 31 = i 28 i 3 = -i

i тисячі шістьдесят три = i +1062 i = i

2. Якщо комплексне число задано в тригонометричної формі.

Тут n може бути як "+" так і "-" (цілим).

3. Якщо комплексне число задано в показовою формі:

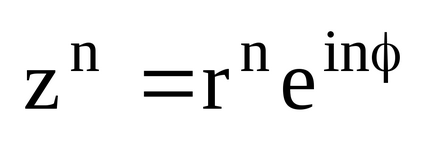
Його рішенням корінь n-го ступеня з комплексного числа z:

.

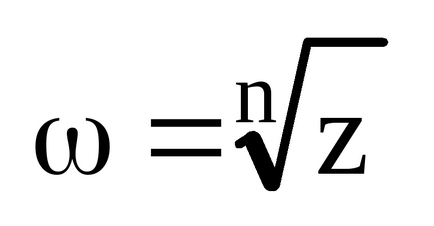
Корінь n-го ступеня з комплексного числа z має рівно n рішень (значень). Корінь з чинного числа n-го ступеня має тільки одне рішення. У комплексних - n рішень.

Якщо комплексне число задано в тригонометричної формі:

z = r (cos

+isin), То корінь n-го ступеня від z знаходиться за формулою:

Ряди. Числові ряди.

Нехай змінна а приймає послідовно значення а1, а2, а3, ..., аn. Таке перенумерували безліч чисел називається послідовністю. Вона нескінченна.

Числовим рядом називається вираз а1 + а2 + а3 + ... + аn + ... =

. Числа а1, а2, а3, ..., аn - члени ряду.

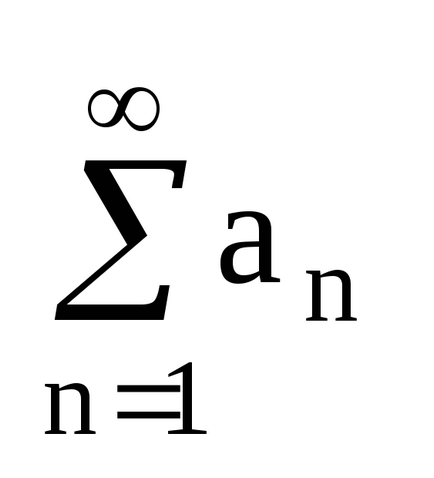
а1 - перший член ряду.

аn - n-ий або загальний член ряду.

Ряд вважається заданим, якщо відомий n-ий (загальний член ряду).

Числовий ряд має нескінченне число членів.

Чисельники - арифметична прогресія (1,3,5,7 ...).

Знаменник - геометрична прогресія. bn = b1 q n-1;

.

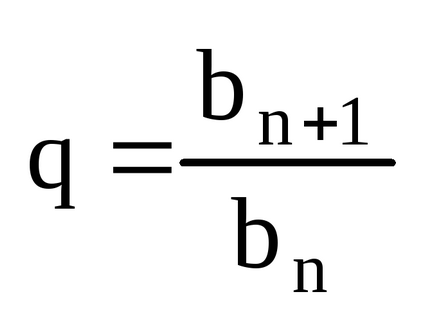
Розглянемо суму перших n членів ряду і позначимо її Sn.

Sn - n-ая часткова сума ряду.

Ряду сходиться. якщо ця межа кінцевий (кінцевий межа S існує).

Ряд розходиться. якщо ця межа нескінченний.

Надалі наша задача полягає в наступному: встановити який ряд.

Одним з найпростіших, але часто зустрічаються рядів є геометрична прогресія.

Геометрична прогресія являетсясходящімсярядом. якщо

, і розходяться, якщо.

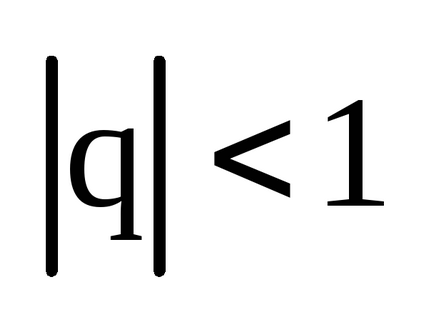
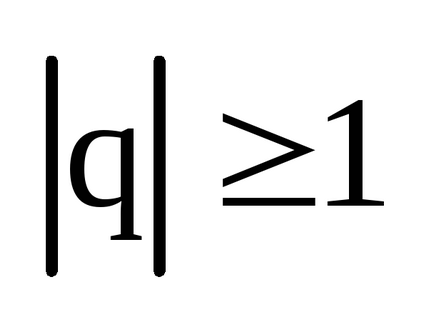
Також зустрічається гармонійний ряд (ряд). Цей рядрасходящійся.

Схожі статті

• Геометричне зображення комплексних чисел