§ 19. Арктангенс і арккотангенс. Рішення рівнянь tgx = а, ctgx = a
У прикладі 2 §16 ми не змогли вирішити три рівняння:
Два з них ми вже вирішили - перше в § 17 і друге в § 18, для цього нам довелося ввести поняття арккосинуса і арксинуса. Розглянемо третє рівняння х = 2.
Графіки функцій у = tg х і у = 2 мають нескінченно багато спільних точок, абсциси всіх цих точок мають вигляд - абсциса точки перетину прямої у = 2 з головною гілкою тангенсоіди (рис. 90). Для числа х1 математики придумали позначення агсtg 2 (читається «арктангенс двох»). Тоді все коріння рівняння х = 2 можна описати формулою х = агсtg 2 + пк.
Що ж таке агсtg 2? Це - число, тангенс якого дорівнює 2 і яке належить інтервалу
Розглянемо тепер рівняння tg х = -2.
Графіки функцій мають нескінченно багато спільних точок, абсциси всіх цих точок мають вигляд абсциса точки перетину прямої у = -2 з головною гілкою тангенсоіди. Для числа х2 математики придумали позначення агсtg (-2). Тоді все коріння рівняння х = -2 можна описати формулою
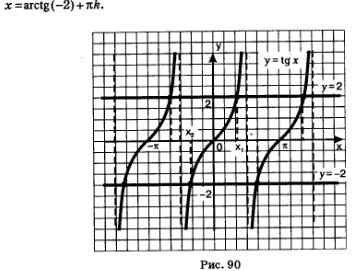
Що ж таке агсtg (-2). Це-число, тангенс якого дорівнює -2 і яке належить інтервалу. Зверніть увагу (див. Рис. 90): х2 = -х2. Це означає, що агсtg (-2) = - агсtg 2.
Сформулюємо визначення арктангенса в загальному вигляді.
Визначення 1. агсtg а (арктангенс а) - це таке число з інтервалу. тангенс якого дорівнює а. Отже,
Тепер ми в змозі зробити загальний висновок про рішення рівняння х = а: рівняння х = а має рішення
Вище ми відзначили, що агсtg (-2) = -агсtg 2. Взагалі, для будь-якого значення а справедлива формула
Приклад 1. Обчислити:

Приклад 2. Вирішити рівняння:
Рішення: а) Складемо формулу рішень:
Обчислити значення арктангенса в даному випадку ми не можемо, тому запис рішень рівняння залишимо в отриманому вигляді.
відповідь:
Приклад 3. Вирішити нерівності:
Нерівність виду можна вирішувати графічно, дотримуючись наступного планам
1) побудувати тангенсоіду у = tg х і пряму у = а;
2) виділити для головної гілки тангейсоіди проміжок осі х, на якому виконується заданий нерівність;
3) враховуючи періодичність функції у = tg х, записати відповідь в загальному вигляді.
Застосуємо цей план до вирішення заданих нерівностей.
Рішення. а) Побудуємо графіки функцій у = tgх і у = 1. На головній гілці тангенсоіди вони перетинаються в точці
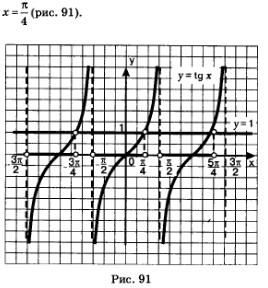
Виділимо проміжок осі х, на якому головна гілка тангенсоіди розташована нижче прямої у = 1, - це інтервал
З огляду на періодичність функції у = tgх, робимо висновок, що заданий нерівність виконується на будь-якому інтервалі виду:
Об'єднання всіх таких інтервалів і являє собою загальне рішення заданої нерівності.
Відповідь можна записати і по-іншому:
б) Побудуємо графіки функцій у = tg х і у = -2. На головній гілці тангенсоіди (рис. 92) вони перетинаються в точці х = агсtg (-2).
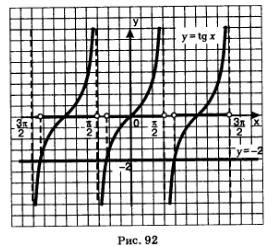
Виділимо проміжок осі х, на якому головна гілка тангенсоіди
Розглянемо рівняння з tg х = а, де а> 0. Графіки функцій у = сtg х і у = а мають нескінченно багато спільних точок, абсциси всіх цих точок мають вигляд: х = х1 + пк, де х1 = агссtg а - абсциса точки перетину прямої у = а з головною гілкою тангенсоіди (рис. 93 ). Значить, агссtg a - це число, котангенс якого дорівнює а і яке належить інтервалу (0, п); на цьому інтервалі будується головна гілка графіка функції у = сtg х.
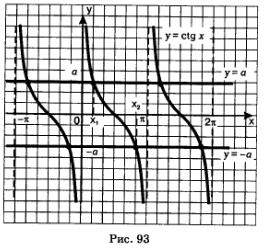
На рис. 93 представлена і графічна ілюстрація рішення рівняння с1tg = -а. Графіки функцій у = сtg х і у = -а мають нескінченно багато спільних точок, абсциси всіх цих точок мають вигляд х = х2 + пк, де х2 = агссtg (- а) - абсциса точки перетину прямої у = -а з головною гілкою тангенсоіди . Значить, агссtg (-а) - це число, котангенс якого дорівнює а і яке належить інтервалу (О, п); на цьому інтервалі будується головна гілка графіка функції У = сtg х.
Визначення 2. агссtg а (арккотангенс а) - це таке число з інтервалу (0, п), котангенс якого дорівнює а.
Отже,
Тепер ми в змозі зробити загальний висновок про рішення рівняння сtg х = а: рівняння ctg х = а має рішення:
Зверніть увагу (див. Рис. 93): х2 = п-х1. Це означає що
Приклад 4. Обчислити:
Рішення: а) Покладемо,
Рівняння сtg х = а практично завжди можна перетворити до вигляду Виняток становить рівняння сtg х = 0. Але в цьому випадку, скориставшись тим, що можна перейти до
рівняння соs x = 0. Таким чином, рівняння виду х = а самостійного інтересу не представляє.
А.Г. Мордкович Алгебра 10 клас
Якщо у вас є виправлення або пропозиції до даного уроку, напишіть нам.
Якщо ви хочете побачити інші коригування та побажання до уроків, дивіться тут - Освітній форум.