Функції двох змінних: \ (f \ left (\ right) \), \ (f \ left (\ right) \), \ (g \ left (\ right) \)
Незалежні змінні: \ (x \), \ (y \), \ (u \), \ (v \)
Малі збільшення: \ (\ Delta \), \ (\ Delta \)
Області інтегрування: \ (R \), \ (S \)
Дійсні числа: \ (a \), \ (b \), \ (c \), \ (d \), \ (\ alpha \), \ (\ beta \)
Полярні координати: \ (r \), \ (\ theta \)
Площа області: \ (A \)
Площа поверхні: \ (S \)
Обсяг тіла: \ (V \)
Маса пластини: \ (m \)
Щільність пластини: \ (\ rho \ left (\ right) \)
Перші моменти: \ (\), \ (\)
Моменти інерції: \ (\), \ (\), \ (\)
Заряд пластини: \ (Q \)
Щільність заряду: \ (\ sigma \ left (\ right) \)
Координати центру мас: \ (\ bar x \), \ (\ bar y \)
Середнє значення функції: \ (\ mu \)
Подвійний інтеграл від функції \ (f \ left (\ right) \) в прямокутній області \ (\ left [\ right] \ times \ left [\ right] \) визначається як межа інтегральної суми (суми Рімана):
\ (\ Require \ large \ iint \ limits_ \ right] \ times \ left [\ right]> \ normalsize \ right) dA> = \ lim \ limits _ \, \ Delta \ to 0 \\ \ text \, \ Delta \ to 0 >> \ sum \ limits_ ^ m ^ n,> \ right) \ Delta \ Delta >>, \)
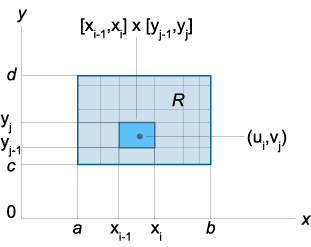
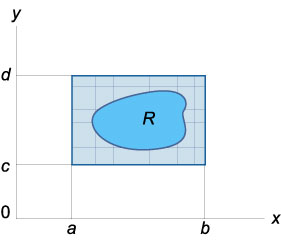
Подвійний інтеграл від функції \ (f \ left (\ right) \) в довільній області \ (R \) визначається як \ (\ large \ iint \ limits_R \ normalsize \ right) dA> = \ large \ iint \ limits_ \ right] \ times \ left [\ right]> \ normalsize \ right) dA>, \)
де прямокутник \ (\ left [\ right] \ times \ left [\ right] \) містить область \ (R \), функція \ (g \ left (\ right) = f \ left (\ right) \), якщо \ (f \ left (\ right) \) знаходиться в \ (R \), і \ (g \ left (\ right) = 0 \) в іншому випадку.
Подвійний інтеграл від суми функцій дорівнює сумі інтегралів від цих функцій:
\ (\ Large \ iint \ limits_R \ normalsize \ right) + g \ left (\ right)> \ right] dA> = \ large \ iint \ limits_R \ normalsize \ right) dA> + \ large \ iint \ limits_R \ normalsize \ right) dA> \)
Подвійний інтеграл від різниці функцій дорівнює різниці інтегралів від цих функцій:
\ (\ Large \ iint \ limits_R \ normalsize \ right) - g \ left (\ right)> \ right] dA> = \ large \ iint \ limits_R \ normalsize \ right) dA> - \ large \ iint \ limits_R \ normalsize \ right) dA> \)
Постійний коефіцієнт можна виносити за знак подвійного інтеграла:
\ (\ Large \ iint \ limits_R \ normalsize \ right) dA> = k \ large \ iint \ limits_R \ normalsize \ right) dA> \)
Якщо \ (f \ left (\ right) \ le g \ left (\ right) \) в області \ (R \), то справедливо нерівність
\ (\ Large \ iint \ limits_R \ normalsize \ right) dA> \ le \ large \ iint \ limits_R \ normalsize \ right) dA> \)
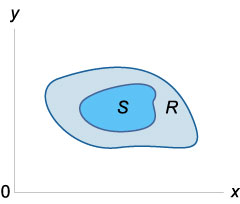
Якщо \ (f \ left (\ right) \ ge 0 \) в області \ (R \) і \ (S \ subset R \), то
\ (\ Large \ iint \ limits_S \ normalsize \ right) dA> \ le \ large \ iint \ limits_R \ normalsize \ right) dA> \)
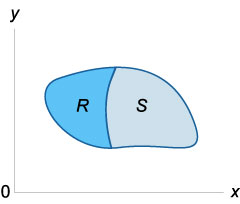
Якщо \ (f \ left (\ right) \ ge 0 \) в області \ (R \), а \ (R \) і \ (S \) - непересічні області, то
\ (\ Large \ iint \ limits_ \ normalsize \ right) dA> = \ large \ iint \ limits_R \ normalsize \ right) dA> + \ large \ iint \ limits_S \ normalsize \ right) dA> \)
Тут \ (\) є об'єднанням областей інтегрування \ (R \) і \ (S \).
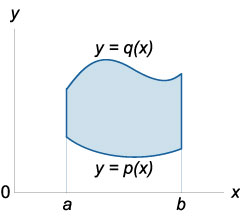
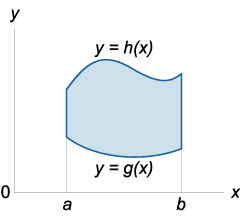
де область інтегрування \ (R \) визначається нерівностями
\ (R = \ left \<\left( \right) \mid a \le x \le b,\;p \left( x \right) \le y \le q\left( x \right)\right\>\).
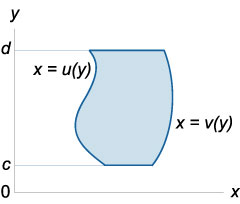
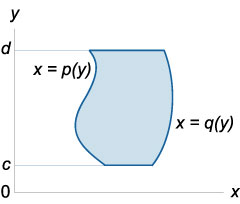
де область інтегрування \ (R \) визначається нерівностями
\ (R = \ left \<\left( \right) \mid u\left( y \right) \le x \le v\left( y \right),\;c \le y \le d \right\>\).
Подвійний інтеграл в прямокутної області
Якщо \ (R \) є прямокутною областю \ (\ left [\ right] \ times \ left [\ right] \), то
\ (\ Large \ iint \ limits_R \ normalsize \ right) dA> = \ large \ int \ limits_a ^ b \ normalsize \ right) dy >> \ right) dx> = \ large \ int \ limits_c ^ d \ normalsize \ right ) dx >> \ right) dy> \)
\ (\ Large \ iint \ limits_R \ normalsize \ right) dxdy> = \ large \ iint \ limits_R \ normalsize = \ left (> \ right) \ left (> \ right) \)
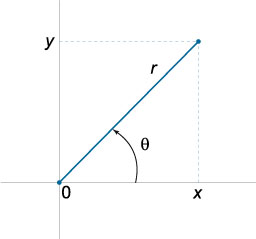
полярні координати
\ (X = r \ cos \ theta, y = r \ sin \ theta \)
Подвійний інтеграл в полярних координатах
Диференціал \ (dxdy \) в полярних координатах визначається виразом
\ (Dxdy = \ left | \ right) >> \ right) >> \ normalsize> \ right | drd \ theta = rdrd \ theta \)
\ (\ Large \ iint \ limits_R \ normalsize \ right) dxdy> = \ large \ int \ limits_ \ alpha ^ \ beta \ normalsize ^ \ normalsize \ right) rdrd \ theta >> \)
Подвійний інтеграл в полярному прямокутнику
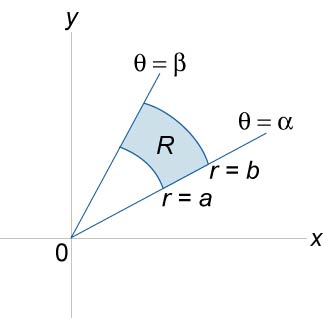
Якщо область інтегрування \ (R \) являє собою полярний прямокутник. заданий нерівностями \ (0 \ le a \ le r \ le b \), \ (\ alpha \ le \ theta \ le \ beta \), де \ (\ beta - \ alpha \ le 2 \ pi \), то подвійний інтеграл дорівнює
\ (\ Large \ iint \ limits_R \ normalsize \ right) dxdy> = \ large \ int \ limits_ \ alpha ^ \ beta \ normalsize \ right) rdrd \ theta >> \)
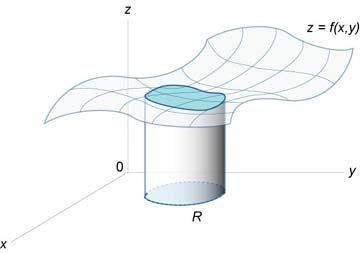
обсяг тіла
\ (V = \ large \ iint \ limits_R \ normalsize \ right) dA> \)
\ (V = \ large \ iint \ limits_R \ normalsize \ right) dA> = \ large \ int \ limits_a ^ b \ normalsize ^ \ normalsize \ right) dydx >> \) Якщо \ (R \) є областю типу \ (II \) і обмежена лініями \ (y = c \), \ (y = d \), \ (x = q \ left (y \ right) \), \ ( x = p \ left (y \ right) \), то
\ (V = \ large \ iint \ limits_R \ normalsize \ right) dA> = \ large \ int \ limits_c ^ d \ normalsize ^ \ normalsize \ right) dxdy >> \)
Обсяг тіла між двома поверхнями
Якщо \ (f \ left (\ right) \ ge g \ left (\ right) \) в області \ (R \), то обсяг тіла між поверхнями \ (\ left (\ right) \) і \ (\ left ( \ right) \) в даній області дорівнює
\ (V = \ large \ iint \ limits_R \ normalsize \ right) - g \ left (\ right)> \ right] dA> \)
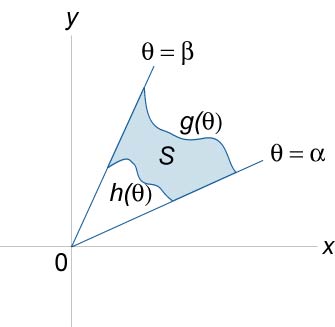
Нехай область \ (S \) задана в полярних координатах в площині \ (Oxy \) і обмежена лініями \ (\ theta = \ alpha \), \ (\ theta = \ beta \), \ (r = h \ left (\ theta \ right) \), \ (r = g \ left (\ theta \ right) \). Нехай також в області \ (S \) задана функція \ (f \ left (\ right) \). Тоді площа області \ (S \) і об'єм тіла, обмеженого поверхнею \ (f \ left (\ right) \), визначаються формулами
\ (A = \ large \ iint \ limits_S \ normalsize = \ large \ int \ limits_ \ alpha ^ \ beta \ normalsize ^ \ normalsize>, \; \; V = \ large \ iint \ limits_S \ normalsize \ right) rdrd \ theta> \)

маса пластини
\ (M = \ large \ iint \ limits_R \ normalsize \ right) dA> \)
Пластина розташована в області \ (R \) і її щільність в точці \ (\ right)> \) дорівнює \ (\ right)> \).
Статичні моменти пластини
Момент пластини щодо осі \ (Ox \) визначається формулою
\ (= \ Large \ iint \ limits_R \ normalsize \ right) dA> \)
Аналогічно, момент пластини щодо осі \ (Oy \) виражається у вигляді
\ (= \ Large \ iint \ limits_R \ normalsize \ right) dA> \)
Моменти інерції пластини
Момент інерції пластини відносно осі \ (Ox \) обчислюється за формулою
\ (= \ Large \ iint \ limits_R \ normalsize \ rho \ left (\ right) dA> \)
Момент інерції пластини відносно осі \ (Oy \) дорівнює
\ (= \ Large \ iint \ limits_R \ normalsize \ rho \ left (\ right) dA> \)
Полярний момент інерції визначається виразом
\ (= \ Large \ iint \ limits_R \ normalsize + \ right) \ rho \ left (\ right) dA> \)
заряд пластини
\ (Q = \ large \ iint \ limits_R \ normalsize \ right) dA> \),
де електричний заряд розподілений по області \ (R \) і його щільність в точці \ (\ right)> \) дорівнює \ (\ right)> \).
Середнє значення функції
\ (\ Mu = \ large \ frac \ iint \ limits_R \ normalsize \ right) dA>, \; \) де \ (S = \ large \ iint \ limits_R \ normalsize \).