Кінцевих збільшень формула Лагранжа
Кінцевих збільшень формула Лагранжа висловлює зв'язок між збільшенням будь-якої неперервної на відрізку [a; b] і диференціюється на інтервалі (а; b) функції y = f (x) і значенням її похідної: де с - деяке число з інтервалу (а; b): a Геометричний сенс формули Лагранжа такий: на дузі графіка даної функції, що з'єднує точки (а; f (a)) і (b; f (b)), знайдеться точка (с; f (c)) (і, можливо, не одна) , в якій дотична до графіка функції паралельна хорді, що з'єднує кінці дуги, - см. рис.
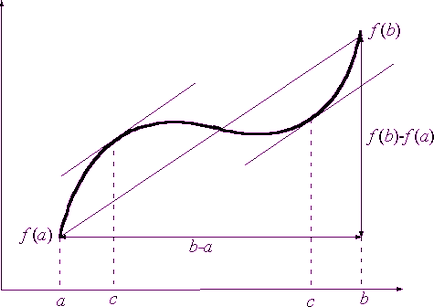
Часто формулу Лагранжа записують в інший, еквівалентній формі: де Θ - невідоме число, залежне, взагалі кажучи, від х0 і від Δх і задовольняє нерівностям 0<Θ <1.
Формула Лагранжа для функції багатьох змінних виглядає так: де 0<Θ <1.
За допомогою формули Лагранжа можна довести наступне її узагальнення - теорему Коші про середнє значення: якщо функції f і g безупинні на відрізку [a; b] і мають похідні на інтервалі (а; b), причому g '(x) ≠ 0 на (а; b), то на інтервалі (а; b) існує така точка с. що В свою чергу, ця теорема дозволяє легко довести одне з важливих співвідношень теорії меж - правило Лопіталя.