Тут під знаком інтеграла стоїть раціональна функція, оскільки підінтегральний вираз є дробом з многочленів. Ступінь многочлена знаменника (3) менше ступеня многочлена чисельника (4). Тому, спочатку необхідно виділити цілу частину дробу.
1. Виділимо цілу частину дробу. Ділимо x 4 на x 3 - 6 x 2 + 11 x - 6.
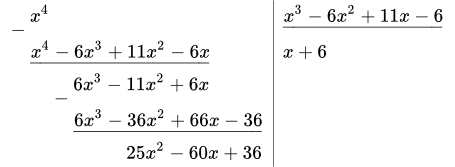
Звідси
.
2. Розкладемо знаменник дробу на множники. Для цього потрібно вирішити кубічне рівняння:
.
Припустимо, що воно має хоча б один цілий корінь. Тоді він є дільником числа 6 (члена без x). Тобто цілий корінь може бути одним з чисел:
1, 2, 3, 6, -1, -2, -3, -6.
Підставами x = 1.
.
Отже, ми знайшли один корінь x = 1. Ділимо на x - 1.
Звідси
.
Вирішуємо квадратне рівняння.
.
Коріння рівняння.
тоді
.
3. Розкладемо дріб на найпростіші.
Отже, ми знайшли:
.
Інтегруємо.
Тут в чисельнику дробу - многочлен нульової ступеня (1 = x 0). У знаменнику - многочлен третього ступеня. оскільки 0 <3. то дробь правильная. Разложим ее на простейшие дроби.
1. Розкладемо знаменник дробу на множники. Для цього потрібно вирішити рівняння третього ступеня:
.
Припустимо, що воно має хоча б один цілий корінь. Тоді він є дільником числа 3 (члена без x). Тобто цілий корінь може бути одним з чисел:
1, 3, -1, -3.
Підставами x = 1.
.
Отже, ми знайшли один корінь x = 1. Ділимо x 3 + 2 x - 3 на x - 1.
Вирішуємо квадратне рівняння:
x 2 + x + 3 = 0.
Знаходимо дискримінант: D = 1 2 - 4 · 3 = -11. оскільки D <0. то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.
2. Розкладемо дріб на найпростіші. Шукаємо розкладання у вигляді:
.
Звільняємося від знаменника дробу, множимо на (x - 1) (x 2 + x + 3).
(2.1).
Підставами x = 1. Тоді x - 1 = 0.
.
Підставами в (2.1) x = 0.
1 = 3 A - C;
.
Прирівняємо в (2.1) коефіцієнти при x 2.
;
0 = A + B;
.
Отже, ми знайшли розкладання на найпростіші дроби:
.
3. Інтегруємо.
(2.2).
Для обчислення другого інтеграла, виділимо в чисельнику похідну знаменника і наведемо знаменник до суми квадратів.
.
Оскільки рівняння x 2 + x + 3 = 0 не має дійсних коренів, то x 2 + x + 3> 0. Тому знак модуля можна опустити.
Тут під знаком інтеграла стоїть дріб з многочленів. Тому підінтегральний вираз є раціональною функцією. Ступінь многочлена в чисельнику дорівнює 3. Ступінь многочлена знаменника дробу дорівнює 4. Оскільки 3 <4. то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
1. Розкладемо знаменник дробу на множники. Для цього потрібно вирішити рівняння четвертого ступеня:
.
Припустимо, що воно має хоча б один цілий корінь. Тоді він є дільником числа 2 (члена без x). Тобто цілий корінь може бути одним з чисел:
1, 2, -1, -2.
Підставами x = -1.
.
Отже, ми знайшли один корінь x = -1. Ділимо на x - (-1) = x + 1.

Отже,
.
Тепер потрібно вирішити рівняння третього ступеня:
.
Якщо припустити, що це рівняння має цілий корінь, то він є дільником числа 2 (члена без x). Тобто цілий корінь може бути одним з чисел:
1, 2, -1, -2.
Підставами x = -1.
.
Отже, ми знайшли ще один корінь x = -1. Можна було б, як і в попередньому випадку, розділити многочлен на. але ми згрупуємо члени:
.
Оскільки рівняння x 2 + 2 = 0 не має дійсних коренів, то ми отримали розкладання знаменника на множники:
.
2. Розкладемо дріб на найпростіші. Шукаємо розкладання у вигляді:
.
Звільняємося від знаменника дробу, множимо на (x + 1) 2 (x 2 + 2).
(3.1).
Підставами x = -1. Тоді x + 1 = 0.
.
Підставами x = -1 і врахуємо, що x + 1 = 0.
;
;.
Підставами в (3.1) x = 0.
0 = 2 A + 2 B + D;
.
Прирівняємо в (3.1) коефіцієнти при x 3.
;
1 = B + C;
.
Отже, ми знайшли розкладання на найпростіші дроби:
.