Повернемося до моделі механічної системи, наведеної в прикладі 3.1. Рівняння нелінійної моделі має вигляд
.
Від рівняння другого порядку можна перейти до автономної системи виду
,
Якщо тепер в системі виключити час t, то отримаємо диференціальне рівняння траєкторій системи на фазовій площині
Останнє рівняння можна переписати так:
Тоді, вважаючи, що при, а. після інтегрування рівняння в межах від до отримуємо рівність
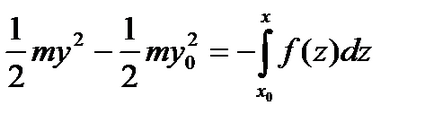
яке можна переписати так:
Зауважимо, що
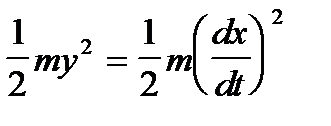
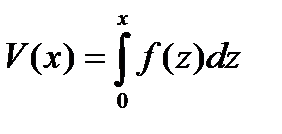
- формула її потенційної енергії. Таким чином, рівняння виражає закон збереження енергії:
де - повна енергія системи.
Ясно, що останнє рівняння - це рівняння фазових траєкторій нелінійної консервативної системи, оскільки воно отримано в результаті інтегрування рівняння
Таким чином, різним значенням Е на фазової площині відповідають різні криві постійної енергії. Стаціонарними точками системи є точки M * (x *, 0), де x * - корінь рівняння. У такому випадку, якщо переписати рівняння закону збереження енергії у вигляді
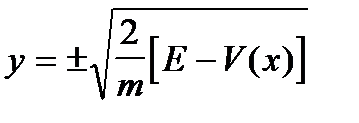
то можна легко побудувати фазові траєкторії.
Проведені міркування загального характеру дають можливість досліджувати рівняння руху маятника в середовищі без опору, яке має вигляд
. де - позитивна постійна.
Оскільки рівняння є окремим випадком рівняння. то його можна інтерпретувати і як рівняння, що описує прямолінійний рух без тертя тіла одиничної маси під дією нелінійної пружини, де відновлює сила дорівнює. В цьому випадку автономна система, відповідна рівнянню, запишеться у вигляді
Особливими точками тут будуть а диференціальне рівняння фазових траєкторій системи набуде вигляду
Поділяючи змінні в останньому рівнянні і інтегруючи, отримаємо рівняння фазових траєкторій
Останнє рівняння є окремий випадок рівняння закону збереження енергії, де. а потенційна енергія задається співвідношенням
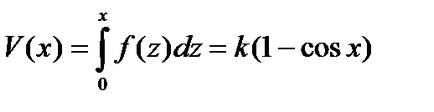
Визначивши значення. ми можемо схематично окреслити картину поведінки траєкторій на фазовій площині, якщо скористатися співвідношенням.
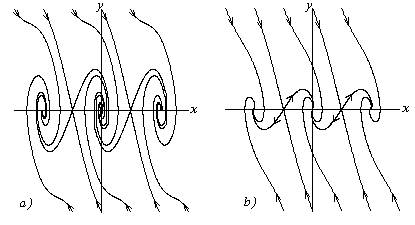
Отриманий фазовий портрет показує (рис. 3.3), що якщо енергія змінюється від до. то відповідні фазові траєкторії виявляються замкнутими і рівняння має періодичні рішення. З іншого боку, якщо. то відповідні фазові траєкторії не є замкнутими і рівняння періодичних рішень не має. Значенням же на фазової площині відповідає фазова траєкторія, яка розділяє два різних типи рухів, таку траєкторію називають сепаратріси. Хвилясті фазові траєкторії, розташовані поза сепаратріси, відповідають обертальним рухам маятника, а замкнуті траєкторії, розташовані в областях, обмежених сепаратріси, - його коливальним рухам.
Мал. 3.3. Фазовий портрет нелінійної консервативної системи
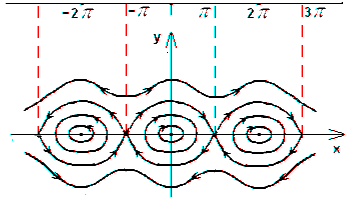
На рис.3.3 видно, що в околиці нерухомих точок. де поведінка фазових траєкторій відрізняється від поведінки фазових траєкторій в околиці нерухомих точок. де
Подивимося тепер, як впливає на поведінку фазових траєкторій консервативної системи лінійне тертя. У цьому випадку рівняння приймає вид
Мал. 3.4.Фазовие портрети консервативних систем з тертям
Така система буде вже неконсервативної. Якщо тертя в ній досить мало, тобто можливі коливання маятника щодо положення рівноваги, то можна показати, що фазові траєкторії такі, як це схематично показано на рис.3.4, a. Якщо тертя не допускає ніяких коливань маятника щодо положення рівноваги, то картина фазових траєкторій матиме вигляд, показаний на рис. 3.4, b.
Якщо тепер порівняти фазовий портрет консервативної системи з останніми двома фазовими портретами неконсервативних систем, то можна помітити, що замкнуті фазові траєкторії при слабкому терті перейшли в спіралі, а при сильному терті - в траєкторії, які входять в особливі точки в певних напрямках.
Мал. 3.4.Фазовие портрети систем з тертям: a - мале тертя; b - велике тертя