Графи і їх подання до пам'яті ЕОМ.
Основні поняття і визначення теорії графів
Теорія графів є розділ математики, який має широке практичне застосування. В її термінах формулюється велике число завдань, пов'язаних з дискретними об'єктами. Такі завдання виникають при проектуванні інтегральних схем і схем управління, електричних ланцюгів, блок-схем програм, в економіці, статистиці, хімії, біології та в інших областях. Теорія графів стає однією з істотних частин математичного апарату кібернетики, мовою дискретної математики.
Завдання 1. Місто Кенігсберг, що розташовувався в східній Пруссії, був побудований в місці злиття двох річок на їх берегах і на двох островах. У місті було сім мостів, які з'єднували острова між собою і з береговими частинами міста (рис.3.1). Необхідно відповісти на питання: чи міг будь-який житель Кенігсберга, вийшовши з дому, пройти по всіх семи мостах міста в точності по одному разу і повернутися додому?
Відповідь на питання, поставлене в даній задачі, повинен бути негативним. Ейлер дав цю відповідь і знайшов критерій існування маршруту, що задовольняє вимогам завдання.

Однак результат, отриманий Ейлером, понад сто років залишався єдиним результатом теорії графів.
Розвиток теорії графів в кінці XIX і початку XX ст. було пов'язано з поширенням уявлень про молекулярному будову речовини і становленням теорії електричних ланцюгів. До 50-х років нашого століття в теорії графів склалися два різних напрямки: алгебраїчне і оптимізаційне.
Наприклад, пошук відповіді на поставлене в завданні 1 питання відноситься до алгебраическому напрямку теорії графів. Змінимо завдання 1.
Завдання 2. Відмінність завдання 2 від завдання 1 полягає в тому, що потрібно знайти маршрут, по якому житель, вийшовши з дому, пройде по кожному мосту хоча б один раз і повернеться додому, причому довжина маршруту повинна бути мінімальною.
Завдання пошуку такого маршруту відноситься до оптимізаційних напрямку теорії графів.
Дамо визначення графа. Нехай V - непорожня множина, V - безліч всіх його двоелементний підмножин. Пара (V, E), де Е ÍV називається графом (неорієнтованим графом).
Граф називається кінцевим. якщо безліч V звичайно. Надалі під терміном "граф" будемо розуміти кінцеві графи.
Елементи множини V називаються вершинами графа, а елементи множини Е називають ребрами графа.
Число вершин графа G = (V, E) називається його порядком.
Виходячи з визначення графа, кожному ребру відповідає двоелементною підмножина вершин. Якщо підмножина v1, v2> відповідає ребру е. То кажуть, що ребро е інцидентне вершин v1 і v2. а вершини v1 і v2смежни. Також кажуть, що ребро е з'єднує вершини v1 і v2. Вершини v1 і v2 називаються кінцевими вершинами ребра е.
Граф можна представити графічно: кожна вершина представляється точкою або окружністю, а кожне ребро представляється відрізком, що з'єднує його кінцеві вершини.
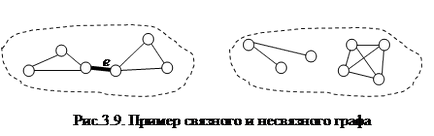
Будь-граф можна розглядати як деяку сукупність зв'язкових графів. Кожен з цих графів називається компонентом вихідного графа.
Незв'язний граф, зображений на рис. 3.9, має два компоненти.
Безліч дуг, виключення яких з графа збільшує число його компонентів, називається розрізом.
Для зв'язкового графа, зображеного на рис. 3.9, розрізом є виділена дуга e. так як її видалення збільшує число компонентів до двох.
Нехай G = (V, E), V ¢ÍV, тоді граф, безліч вершин якого збігається з V ¢, а безліч дуг включає всі дуги безлічі E з кінцевими вершинами в V ¢, називається подграфом графа G. породженим V ¢.
Нехай E ¢ÍE. тоді граф, для якого безліч дуг збігається з E ¢, а безліч вершин включає вершини, інцидентні дуг з E ¢, називається подграфом графа G, породженим E ¢.
Граф називається повним, якщо будь-які дві його вершини суміжні.
Граф G називається порожнім. якщо в ньому немає ребер.
Граф, який не містить циклів, називається ациклічним.
Зв'язний неорієнтований ациклический граф називається деревом. безліч дерев називається лісом.
Якщо ребра, складові дерево, замінити орієнтованими дугами, то отримаємо орієнтоване дерево. Якщо з контексту ясно, про яке дереві йдеться, то в подальшому слово «орієнтоване» будемо опускати.
Для орієнтованого дерева має сенс ввести поняття кореня. Мінімальна по потужності безліч вершин орієнтованого дерева, з яких існують шляхи в усі решта вершини, будемо називати множиною коренів.
Покриває (остовне) деревом графа G називається дерево, що є подграфом графа G і містить всі його вершини.
Якщо граф G незв'язний, то безліч, що складається з основних дерев кожної компоненти, називається покриває (остовне) лісом.
Узагальненням графа є гіперграф.
У гіперграфах. на відміну від графа, ребрами можуть бути не тільки двоелементний, але і будь-які підмножини вершин.
Подібні об'єкти в математиці відомі давно, однак введення терміну "гіперграф" пов'язано з успішним розглядом на них ряду важливих понять і методів теорії графів.
3.1.2. П редставленіе графів в пам'яті ЕОМ
Будь-граф може бути представлений в матричної формі.
Для графа, зображеного на рис. 3.5, матриця суміжності представлена в таблиці 3.1.
Відзначимо, що для неорієнтованих графів матриця суміжності симетрична щодо головної діагоналі, тобто в пам'яті ЕОМ досить зберігати тільки половину матриці.
Матриця суміжності графа, зображеного на рис.3.5
На практиці дуже часто матриці, що представляють графи, бувають сильно вбраними, тобто містять багато символів "0" або "¥". Це призводить до невиправданих витрат пам'яті при зберіганні цих матриць в ЕОМ.
Обсяг пам'яті можна істотно зменшити, якщо упаковувати матриці в списки гніздового типу.
Приклад упаковки розглянутої матриці ваг (табл. 3.3) в список гніздового типу, реалізований на трьох векторах (масивах), наведено на рис.3.10.
Для знаходження вершин, суміжних i -ої вершини, і ваг відповідних дуг по такій структурі необхідно обчислити початковий In і кінцевий Ik індекси в векторах V і S за формулами
Для зберігання упакованої таким чином матриці ваг знадобиться 42 осередки пам'яті, займаних масивами V, S і U. неупаковані матриця займала 10'10 = 100 осередків пам'яті.
Рис.3.10. Упаковка матриці ваг (табл. 4.3) в список гніздового типу
При реалізації алгоритмів, в яких змінюється вихідний граф (додаються або видаляються вершини і так далі), для зберігання графів іноді зручно застосовувати списки суміжності. Список суміжності можна реалізувати шляхом створення лінійного списку з n лінійних списків, де n - число вершин графа.
Для графа, зображеного на рис. 3.7, список суміжності представлений на рис. 3.11.

Ще один спосіб зберігання графів - це список ребер, тобто список, в якому перераховані всі ребра графа.
Список ребер графа, представленого на рис. 3.7, наведено на рис. 3.12.
Список ребер реалізований на трьох масивах і займає 48 осередків. Можна також замість масивів використовувати спискові структури.
Вибір того чи іншого способу кодування графа і структури даних для його реалізації залежить як від конкретного завдання, алгоритму її рішення, можливих вхідних даних, так і від індивідуальних схильностей програміста.