
Головна | Про нас | Зворотній зв'язок
Найважливішими прикладами руху частинок в потенційних ямах є рух нуклонів в ядрах, електронів в атомах і молекулах. Основні закономірності фінітного руху частинок можна досліджувати на прикладі, коли форма потенційного рельєфу має вигляд прямокутної нескінченно глибокої ями шириною а. На інтервалі (0, а) потенційну енергію приймемо рівною нулю, а поза цим інтервалом вона звертається в нескінченність (Рис. 2.1). Внаслідок цього частка при своєму русі не може вийти за межі відрізка (0, а) або, як кажуть, частка перебуває в нескінченно глибокій потенційній ямі шириною а.
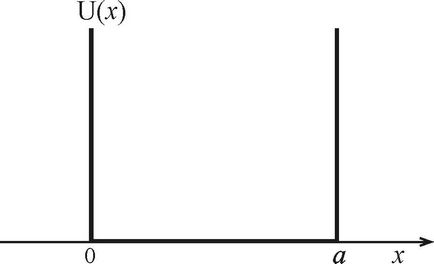
Мал. 2.1. Прямокутна потенційна яма нескінченної глибини
Оскільки ймовірність знаходження частинки поза безмежно глибокої ями дорівнює нулю, то хвильова функція поза інтервалу (0, а) дорівнює нулю. Таким чином, отримуємо граничні умови для вирішення рівняння Шредінгера:
Оскільки потенційна енергія U (x) не залежить від часу, то для обчислення хвильових функцій частки необхідно вирішити стаціонарне одномірне рівняння Шредінгера з нульовим потенціалом на дні ями,. тобто
Наведемо рівняння (2) до канонічного вигляду:
є величина з розмірністю хвильового числа: м - 1. Характеристичне рівняння: має комплексні корені. Загальне рішення диференціального рівняння (3) запишемо у вигляді
Стаціонарне рівняння Шредінгера, як відомо, містить осциллирующий з частотою тимчасової множник
. ()
Перший доданок являє собою «падаючу» хвилю де Бройля з амплітудою А. хвильовим числом і частотою. а другий доданок - «відображену» хвилю де Бройля, тобто хвилю, що поширюється в протилежному напрямку. Ці хвилі когерентні, так як вони мають однакову довжину хвилі. Зазвичай плоскі хвилі де Бройля записують без тимчасового множника, тобто у вигляді (5).
Підставляючи рішення (5) в граничну умову. маємо і Застосовуючи формулу Ейлера. отримаємо
де - нормувальний множник, який обчислюється з умови нормування. Підставляючи (6) в умова нормування
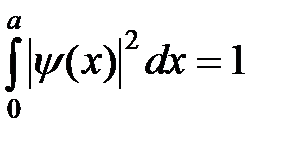
Підставами тепер рішення (6) у другу граничну умову: і отримаємо звідки. де n приймає натуральний ряд чисел. Таким чином, хвильове число k - квантів, тобто приймає дискретний ряд значень
Підставляючи (7) в (6) остаточно маємо для хвильових функцій, що описують стан частинки в нескінченно глибокій потенційній ямі шириною а:
Для того, щоб отримати спектр енергії частинки, підставимо знайдені значення хвильових чисел (7) в формулу (4):
Як видно, рішення (8) представляє стоячу хвилю де Бройля, яка утворилася в результаті інтерференції «падаючої» і «відбитою» когерентних хвиль де Бройля, що визначаються співвідношенням (5) або (). Умова освіти стоячій хвилі (7) запишемо в термінах довжини хвилі де Бройля враховуючи, що. тоді отримаємо
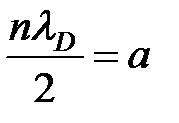
тобто стояча хвиля утворюється за умови, коли на ширині ями укладається ціле число довжин півхвиль, рівне квантовому числу n. Щільність ймовірності, тобто ймовірність виявити частинку на одиничному відрізку ями, дорівнює відповідно
На рис. 2.2 представлені хвильові функції частинки і відповідні щільності ймовірності перших станів при n = 1,2,3 і при n = 20 >> 1.
Видно, що при невеликих квантових числах, розподіл ймовірностей для частинки в ямі носить сильно нелінійний характер, але з ростом квантового числа функція щільності ймовірності має тенденцію бути більш однорідною і в межі великих квантових чисел. що відповідає граничному переходу до класичної задачі. Дійсно при великих квантових числах n >> 1, довжина хвилі частинки стає набагато меншою ширини ями <<а. что соответствует условию применимости классического описания, в котором волновые свойства частицы не учитываются. В тоже время квантовомеханическое описание используется в случае соизмеримости длины волны де Бройля частицы и характерного размера системы, ограничивающего движение частицы (ширины ямы), что соответствует случаю малых квантовых чисел.
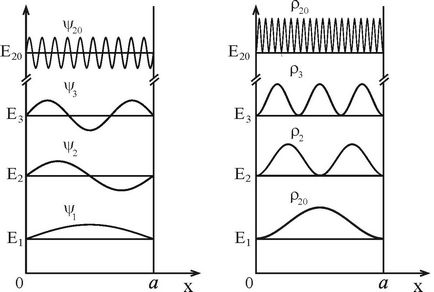
Мал. 2.2. Спектр енергії, хвильові функції (а) і розподіл щільності ймовірності (б) частки в нескінченно глибокій прямокутній потенційній ямі