транскрипт
1 Лабораторна робота 9 ЛІНІЙНІ ОПЕРАТОРИ І функціональний в нормованих просторах. НОРМА лінійного ОПЕРАТОРА і функціонал. Про З Н О В Н И Е П О Н Я Т І Я І Т Е Про Р Е М И Визначення. Нехай і векторні простору над одним і тим же полем (= R або C). Відображення. з областю визначення D () і областю значень R () називається лінійним оператором з в, якщо для будь-якого, y і. ) (Y) y (адитивність); ) () (Однорідність). Позначимо через (,) безліч всіх лінійних операторів з в, область визначення яких збігається з E. Для, (,) і визначимо оператори, (,) формулами. def def (); (). Тоді (,) стає векторним простором. В окремому випадку, коли (поле є векторним простором!), Елементи (,) називається лінійними функціоналом на. Нехай тепер на i визначені норми i (i,), тобто нормовані простору (, Norm). Визначення. Оператор (,) називається обмеженим оператором з в, якщо існує така постійна c, що для будь-яких має місце рівність c. Визначення. Нормою оператора (,) називається число def sup. Можна показати, що c з визначення. є точна нижня грань множини всіх констант
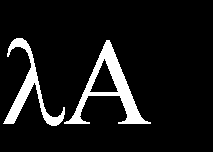
2 ТЕОРЕМА. Нехай (,), де, Norm. Тоді наступні твердження еквівалентні. ) Оператор є безперервним оператором з в; ) Оператор є обмеженим оператором з в; ). Нехай, (,), де, Norm. Чи справедливі співвідношення:); ); ). Тому, якщо, обмежені оператори, то оператори, теж обмежені. Отже, якщо позначати через L (,) безліч всіх лінійних обмежених операторів з в, то L (,) векторних подпространством (,). є ТЕОРЕМА. Якщо Norm, а Банахів (Ba), то L (,) Ba. Все сказане відноситься і до функціоналом. В цьому випадку, норма на, тому функціонал f (,) називається обмеженим на Norm, якщо існує така постійна c, що f () c для будь-яких. Тоді норма функціоналу f є число def f sup f () if c. f () c. Так як Ba, то по теоремі L (,) Ba. Визначення. Банахів простір L (,), що складається з лінійних обмежених функціоналів на, будемо позначати через * і називати зв'язаним простором до E. Література: [] стор. 9-56; [] Стор. 8-5; [5] стор З А Д А Ч І
3. Нехай, Norm. Знайти область визначення def D (). оператора і встановити, чи збігається вона с. Якщо D () Norm, то з'ясувати, чи є оператор лінійним обмеженим оператором з D () в? E. l c. c l. L [,] L [,] () (t) t (s). L [,] L [,] () (t) (t) .5 L [,] L [,] () (t) (t) .6 C [,] C [,] () (t) ( t) .7 C [,] C () [,] () (t) (t) .8 C () [,] C [,] () (t) (t) .9 c R. l l. l l. L [-,] L [-,] () (t) (5 t). C [,] R () (t) () (). L [-,] L [-,] () (t) t (s) .5 L `[,] L [,] () (t) (t) Рішення задачі.5. Знайдемо D () L [,]. L [,] область визначення оператора. Оскільки 8 (t) (t), то D (A) = L L
if ($ this-> show_pages_images $ Page_num doc [ 'images_node_id']) 
4 (y) y. Тому оператор не є лінійним на D (), а отже і обмеженим. -5. Чи задає дана формула лінійний обмежений оператор. У разі обмеженості оператора, знайти його норму. Оператор множення. C [,] C [,] () (t) (t t) (t). C [-,] C [,] () (t) (t t) (t). L [,] L [,] () (t) t (t). L [,] L [,] () (t) (tt) (t) .5 L [-,] L [-,] () (t) t (t) .6 L [-,] L [, ] () (t) t (t) .7 L [,] L [,] () (t) (t) (t) .8 C [-,] C [,] () (t) (tt) (t) .9 L [-,] L [-,] () (t) t (t). C () [-,] C [,] () (t) si t (t). L [,] L [,] () (t) t (t). C [-,] C [-,] () (t) (t) (t), t [, [(t t) (t), t [,]. C [,] L [,] () (t) t (t) t (t), t [,]. L [-,] L [-,] () (t), t [, [Рішення завдання. Область визначення оператора D () L [-,] (твір (t) на безперервну функцію не «виводить" це твір з L [-,]). Лінійність оператора очевидна. Так як для L [-,]
5 L t t t [,] () () L
6. L [,] L [,] () (t) t (t). L [-,] L [,] () (t) t (t) Рішення завдання. Нехай L [-,]. Тоді t (t) L [,] u t du t t u = du (u) (u) (u) (u) du u (u) du L [,]. З останнього співвідношення випливає, що D () L [-,]. Очевидно, що оператор лине і з доведеного нерівності випливає, що A обмежений і. Розглянемо послідовність функцій (t) (t) L [,]. Тоді [,] L [,] sup L [,] sup sup (u) du L [,] L [,] sup 5 Отже 5 sup 5 5. З огляду на попереднє, маємо. Оператори в просторах послідовностей l l (.) 5
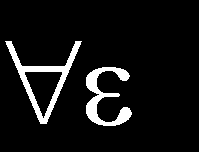
7. l l (.). c c (.). l l. 5 l l. 6 l l. 7 l l. 8 c c. 9 c si c. si. l l (.). l c. l l. l c (.). l l. де M, N Рішення завдання. Так як для l sup sup, то D () l і лінійність оператора перевіряється без праці. Звідси ж маємо sup I. У силу визначення точної верхньої межі, для існує таке, що I. Тоді для l (.) L, l і sup l I. Переходячи в останньому нерівності до межі при I sup, тобто sup 5. Інтегральний оператор отримаємо 6
8 5. L [,] L [,] () (t) ts (s) 5. L [,] L [,] () (t) (t) s (s) 5. C [,] L [ ,] () (t) (ts) (s) 5. L [,] C [-,] () (t) ts (s) 5.5 L [,] lt (t). t (t), L [,] l t (t). t (t), L [,] L [-,] () (t) ts (s) 5.8 C [-,] L [,] () (t) tsig s (s) 5.9 L [,] L [ ,] () (t) ts (s) 5. L [,] L [,] () (t) (t) s (s) 5. C [,] L [,] () (t) sig ( s) (s) t () 5. L [-,] L [,] () (t) (t) s (s) 5. C [,] C [,] () (t) (ts) ( s) 5. L [,] lt (t). t (t). 7
9 Рішення завдання 5. Нехай L [,]. Тоді l t (t) (t) L. [,] Тому D () L [,] і лінійність оператора випливає з лінійності інтеграла. З встановленого нерівності слід тамкже, що 8. З іншого боку, якщо (t) (t), то, і L, [,] sup L [,] l sup l sup t sup () 8. Отже, Нехай Ba, До або С. задає дана формула лінійний обмежений функціонал f. У разі позитивної відповіді, знайти його норму. f 6. c З f () lim 6. l R f () 8
10 6. l R 6. c З 6.5 l R 6.6 c R f () f () (i) f () f () 6.7 l З f () 6.8 c R f () l R f () 6. l R f () 6. l З f () i 6. l З f () 6. c R f () lim 6. l З f () Рішення завдання 6. Лінійність функціонала перевіряється без праці. Нехай l. Тоді застосовуючи нерівність Коші-Буняковського, матимемо. l f () () Звідси D (f) l, функціонал f обмежений на l і f що константа c. Покажемо, є найменшою з усіх можливих у нерівності (). Для цього достатньо вказати такий ненульовий елемент l, для якого () стає ланцюжком рівності. Рівність в () може порушується після застосування нерівності Коші-Буняковського. Останнє не порушує рівності, якщо * 9
11 N. f () * * Візьмемо, тоді для * (.), 8. Отже, f. 7. L [,] R f () t (t) 7. L [,] C f () it (t) 7. C [,] R f () () () 7. C [,] R f () lim (t) 7.5 L [,] C f () t (t) 7.6 L [-,] R f () t (t) 7.7 L [,] R f () t (t) 7.8 L 6 [ ,] R f () t (t) 7.9 C () [,] C f () () i () 7. C () [,] R f () (t) (t) 7. C () [ -,] C f () () 7. C () [,] C f () i () () 7. L [,] R f () t (t) 7. L [,] C f () it (t) f * і
12 Рішення завдання 7. Лінійність функціонала випливає з лінійності інтеграла. Нехай L [,]. Тоді зробивши заміну змінних в інтегралі, а потім застосовуючи нерівність Коші-Буняковського, отримаємо f () t (t) u t u t udu u u du u du u du () (). () Отже, D (f) l, функціонал обмежений і f. Візьмемо * (u) u (чому?), Тоді з () маємо * * f () u u du u du. Звідси випливає, що константа c можливих. Тому f в () є найменшою з усіх Варіанти завдання Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант
13 Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Варіант Д О П О Л Н І Т Е Л Ь Н И Е З А Д А Ч І І У П Р А Ж Н Е Н І Я. Довести, що функціонал f. (T) (t) R (t) C () [,] безперервний. 5. Довести, що функціонал f. (T) (t) R лине і необмежений на лінійному підпросторі C () [,] нормованого простору C [,]. 6. В l розглянемо оператор (.) (.). За яких він обмежений на l? Знайти його норму. 7. Нехай-оператор множення на обмежену вимірну функцію a (), що діє в просторі L p (,). Довести, що обмежений і знайти його норму. 8. Знайти норму тотожного оператора, що діє з Lp [a, b] в Lq [a, b] при p q.
Лабораторна робота СПЕКТР ОПЕРАТОРА. Про З Н О В Н И Е П О Н Я Т І Я І Т Е Про Р Е М И Нехай. обмежений лінійний оператор в банаховому просторі над полем. C. Визначення. Точка C називається регулярною
1 Функції безперервні на відрізку (теореми Больцано-Коші, Вейєрштрасса, Кантора). Функціонали безперервні на компакті. 1.1 Теорема про проміжні значення Теорема 1. (Больцано-Коші) Нехай функція f неперервна на відрізку [a, b], причому f (a) f (b). Тоді для будь-якого числа C, укладеного між f (a) і f (b) знайдеться точка γ (a, b), що f (γ) = C. Доказ. Нехай, наприклад, f (a) = A 0. Для доведення теореми достатньо показати, що існує така точка γ (a, b), що g (γ) = 0. Розділимо відрізок [a, b] точкою x 0 на два рівних по довжині відрізка, тоді або g (x 0) = 0 і, отже, шукана точка γ = x 0 знайдена, або g (x 0) 0 і тоді на кінцях одного з отриманих проміжків функція g приймає значення різних знаків, точніше, на лівому кінці значення менше нуля, на правому - більше. Позначимо цей відрізок [a 1, b 1] і розділимо його знову на два рівних по довжині відрізка і т.д. В результаті, або через кінцеве число кроків прийдемо до шуканої точці γ, в якій g (γ) = 0, або отримаємо послідовність вкладених відрізків [a n, b n] по довжині прагнуть до нуля і таких, що g (a n)