функція Ейлера

Попередня ↔ Наступна

Функція Ейлера φ (а) визначається для всіх натуральних чисел а і являє собою кількість натуральних чисел взаємно простих з а. і не перевищують а. При цьому вважається, що φ (1) = 1. Обчислюється ця функція по формулі

де

- прості подільники в канонічному розкладанні чіслаа.

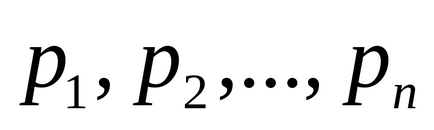
Число чисел, що становлять наведену систему відрахувань одно φ (m).

Загальна властивість повної і наведеної системи відрахувань

якщо числа

являють собою повну (k = m) або наведену (k = φ (m)) систему відрахувань по модулю m. то і числа

, де

, так само є повною або наведену систему відрахувань по модулюm.

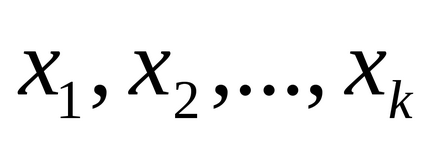
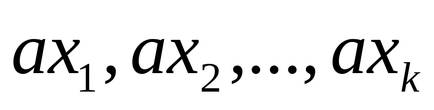
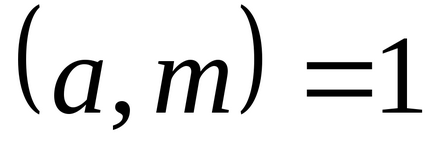
Показати, що числа 25, -20,16,46, -21,18,37, -17 складають повну систему відрахувань по модулю 8.

Утворити повну систему найменших невід'ємних чисел

, ,

,,,

,,.

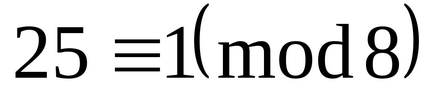
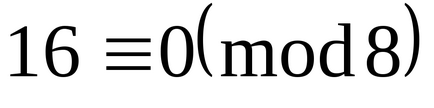
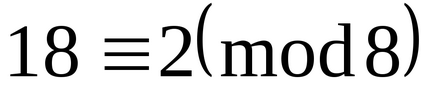
Отже, дані числа 0,1,2,3,4,5,6,7 утворюють повну систему відрахувань по модулю 8.

Теореми Ейлера і Ферма

Нехай x пробігає наведену систему відрахувань

, де

складену з найменших невід'ємних лишків. Найменші невід'ємні відрахування

чіселax будуть побігати ту ж систему, але розташовану (в загальному випадку) в іншому порядку. Перемноживши почленно порівняння. Звідки отримаємо. Звідки, ділячи обидві частини на твір, отримаємо

або.

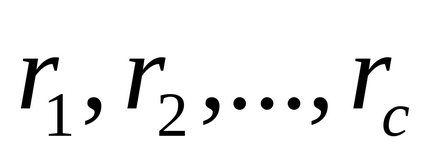
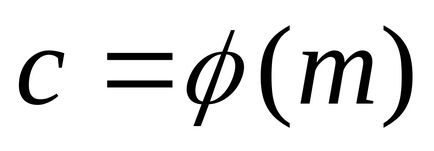
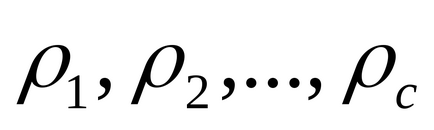
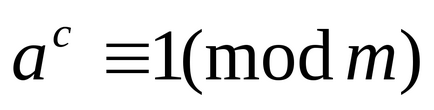
При простому p і a. що не діляться на p. маємо

Ця теорема є окремим випадком теореми Ейлера, при m = p. З (2) можна легко отримати дуже важливе порівняння

справедливе при всіх цілих а. так як воно вірно і при a кратному p.

Перевірити теорему Ейлера при a = 5 і.

Знайти залишок від ділення

на 45.

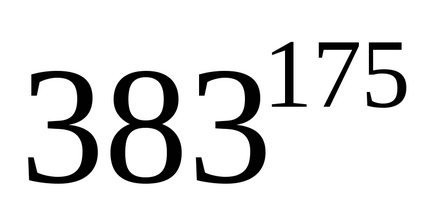
Так як, то. Так як

і (23,45) = 1, то по теоремі Ейлера

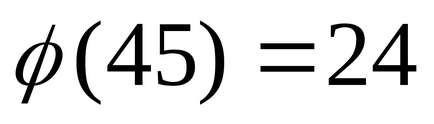
Відповідь: шуканий залишок дорівнює 32.

Порівняння першого ступеня (рішення задач)

Вирішити способом Ейлера порівняння. Правильність відповіді перевірити підстановкою.

(3,5) = 1, значить, дане порівняння має єдине рішення (в сенсі класу чисел x по modm). За формулою Ейлера маємо,

, тоді отримаємо

або або.

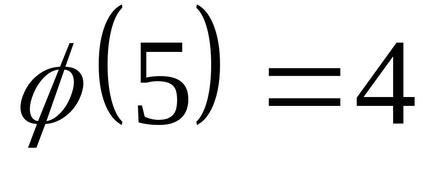
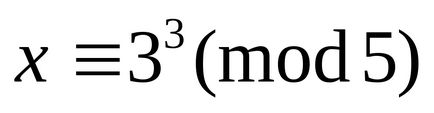
Вирішити способом Ейлера порівняння.

(5,10) = 5, але 7 не ділиться на 5, значить, дане порівняння не має рішень.

Вирішити способом Ейлера порівняння.

Так як (25,17) = 1, то дане порівняння має рішення. Дане порівняння рівносильне порівнянню. За формулою Ейлера маємо.

, тоді

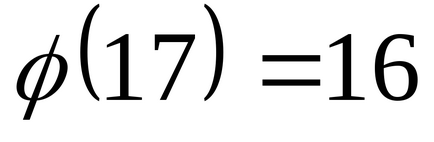
Вирішити одним із способів порівняння

(12,15) = 3. Значить, дане порівняння має 3 рішення (в сенсі класів). Розглянемо порівняння

яке отримано з даного після скорочення на 3.

За формулою Ейлера маємо ,.

Ми знайшли рішення порівняння (2). Рішення порівняння (1) знаходиться за формулою, k = 0,1,2.

; ; .

Приписати праворуч до числа 523 такі три цифри, щоб отримане шестизначне число ділилося на 7,8,9.

Нехай приписуване число x. тоді, откудаілі. Значеніеx буде тризначним числом при t = 0 і t = 1. отримуємо

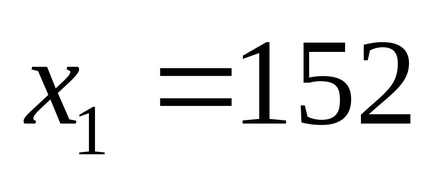
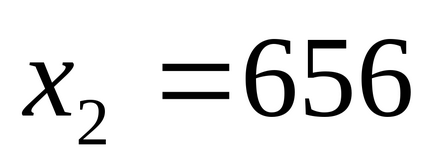
523152 ділиться на 7,8,9;

523656 ділиться на 7,8,9.

функція Ейлера

Порівняння першого ступеня (рішення задач)

Схожі статті