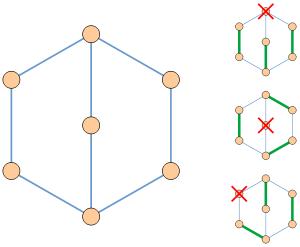
Фактор-критичний граф разом з найбільшими паросочетание подграфов, отриманих видаленням однієї з вершин.
Фактор-критичний граф (або майже поєднується граф.) - це граф з n вершинами, в якому кожен підграф з n - 1 вершинами має зроблене паросполучення. (Досконале паросочетание в графі - це підмножина ребер з властивістю, що кожна з вершин графа є кінцевою вершиною в точності одного ребра з підмножини.)
Поєднання, що покриває всі вершини, крім однієї, називається майже зроблене паросполучення. Таким чином, еквівалентно, фактор-критичний граф - це граф, в якому існують майже досконалі паросполучення, які не містять будь-яку з вершин.
Три графа дружніх відносин. приклади негамільтонових фактор-критичних графів
Будь-який цикл непарної довжини є фактор-критичним. як і будь-який повний граф з непарним числом вершин. Більш загально, будь гамільтонів граф з непарним числом вершин є фактор-критичним. Графи дружніх відносин (графи, утворені сполученням набору трикутників з однією спільною вершиною) дають приклади графів, фактор-критичних, але не гамільтонових.
Якщо граф G є фактор-критичним, то він є мичельскіаном графа G. Наприклад, граф Грёча. мичельскіан циклу з п'ятьма вершинами, є фактор-критичним.
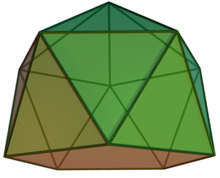
Будь вершинно 2-зв'язний граф без колишній з непарним числом вершин є фактор-критичним. Наприклад, граф з 11 вершинами, утворений вершинами правильного ікосаедра (граф скручених подовженою п'ятикутної піраміди [en]), є як 2-зв'язковим, так і вільним від колишній, так що він є фактор-критичним. Цей результат слід прямо з більш фундаментальної теореми, що будь-який зв'язний граф без колишній з парним числом вершин має зроблене паросполучення.
Фактор-критичні графи можна описати кількома різними шляхами, відмінними від визначення як графи, видалення будь-якої вершини яких дозволяє зроблене паросполучення:
- Тібор Галлай [en] довів, що граф є фактор-критичним тоді і тільки тоді, коли він зв'язний і для будь-якої вершини v графа, існує найбільша паросочетание. яке не включає v. З цієї властивості випливає, що граф повинен мати непарне число вершин і що будь-який найбільше паросполучення має включати всі, крім однієї вершини.
- Ласло Ловас довів, що граф є фактор-критичним тоді і тільки тоді, коли він має непарну вушну декомпозицію. розбиття ребер на послідовність подграфов, кожен з яких є шляхом або циклом непарної довжини, і перший підграф в послідовності є циклом, кожен шлях в послідовності має кінцеві, але не внутрішні, вершини на попередніх подграфа, а кожен цикл, відмінний від першого, має рівно одну вершину, спільну з попередніми подграфа. Наприклад, граф на ілюстрації може бути розбитий таким чином на цикли з п'ятьма ребрами і шляхи з трьома ребрами. У разі, коли майже зроблене паросполучення фактор-критичного графа також задано, вушне розкладання може бути вибрано таким чином, що кожне вухо по черзі проходить ребра паросполучення і ребра, що не входять в паросочетание.
- Граф є також фактор-критичним тоді і тільки тоді, коли його можна звести до графу з єдиною вершиною шляхом стягування циклів непарної довжини. Більш того, в цьому випадку можна вибрати кожен цикл в послідовності таким чином, щоб він містив вершину, отриману шляхом стягування попереднього циклу. Наприклад, якщо стягувати вуха вушного розкладання в порядку, заданому розкладанням, то кожен раз стягують вухо утворює непарний цикл, так що опис за допомогою вушного розкладання можна використовувати для пошуку послідовності непарних циклів для стягування. Назад, з послідовності стягування непарних циклів, що містять вершини, отримані на попередніх стягування, можна утворити вушне розкладання, в якому вуха утворюють безлічі стягуються ребер.
- Припустимо, що граф G заданий разом з обраної вершиною v і паросочетание M. покриває всі вершини, відмінні від v. Тоді G є фактор-критичним тоді і тільки тоді, коли існує безліч шляхів в G. складаються з черзі йдуть ребер з паросочетание і ребер, що не входять в паросочетание, що з'єднують вершину v з усіма іншими вершинами графа G. Грунтуючись на цій властивості, можна визначити за лінійний час. чи є граф G з заданим майже зроблене паросполучення фактор-критичним.
Фактор-критичні графи повинні завжди мати непарне число вершин і повинні бути реберно 2-зв'язковими (тобто вони не можуть мати будь-якого моста). Однак вони не обов'язково вершинно 2-зв'язні. Графи дружніх відносин дають контрприклад. Фактор-критичний граф не може бути дводольним. оскільки в дводольному графі з майже зроблене паросполучення тільки вершини, які можуть бути видалені для отримання графа з зроблене паросполучення, знаходяться на більшій стороні двудольного графа.
Будь вершинно 2-зв'язний фактор-критичний граф з m ребрами має щонайменше m різних майже зроблене паросполучення, і, більш загально, будь-який чинник-критичний граф з m ребрами і c блоками (зв'язкових компонент з 2 вершин) має щонайменше m - c + 1 різних майже зроблене паросполучення. Графи, для яких ці кордони точні, можна описати як такі, що вушне розкладання специфічного виду.
Будь-зв'язний граф можна перетворити в фактор-критичний граф шляхом стягування досить багато ребер. Мінімальний набір ребер, які потрібно стягнути, щоб зробити заданий граф G фактор-критичним, утворює базис матроід. факт, з якого випливає, що працює за поліноміальний час жадібний алгоритм може бути використаний для пошуку найменшого зваженого безлічі ребер, стягування яких робить граф фактор-критичним. Ранній алгоритм стягування мінімального числа (невиважених) ребер для отримання фактор-критичного графа можна знайти в статті Франка.
Квітка - це фактор-критичний підграф більшого графа. Квітки грають ключову роль в алгоритмах [en] Едмондс [en] пошуку найбільшого паросполучення і мінімального зваженого досконалого поєднання в недвудольних графах.
В комбінаториці багатогранників фактор-критичні графи грають важливу роль при описі фасет багатогранників паросочетание заданого графа.
Узагальнення та пов'язані концепції Правити
Кажуть, що граф k-фактор критичний, якщо будь-яка підмножина з n - k вершин має зроблене паросполучення. При такому визначенні майже поєднується (en: hypomatchable) граф є 1-фактор-критичним. Навіть більше загально, граф є (a, b)-фактор-критичним, якщо будь-яка підмножина з n - k вершин має r-фактор, тобто він є набором вершин r -Регулярно подграфа заданого графа.
Коли говорять про критичний графі (без уточнення k-), зазвичай мають на увазі граф, видалення будь-якої вершини якого призводить до зменшення числа квітів, необхідних для розмальовки графа. Поняття критичності використовується значно ширше в теорії графів для графів, в яких видалення будь-якої вершини змінює якесь властивість графа. Критичний по сполученням граф - це граф, для якого видалення будь-якої вершини не змінює розміру найбільшого паросполучення. Згідно Галлай, критичні за сполученням графи, це в точності графи, в яких будь-яка зв'язкова компонента є фактор-критичної. Доповнення критичного графа обов'язково критично по сполученням, факт, який використовував Галлай для доказу нижньої межі числа вершин критичного графа.
Поза теорії графів поняття фактор-критичності має розширення на матроід шляхом визначення типу вушного розкладання на матроід. Матроід є фактор-критичним, якщо він має вушне розкладання, в якому всі вуха непарні.