Завдання Коші для рівняння теплопровідності





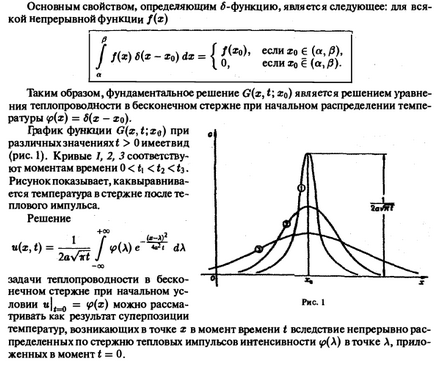
Розглянемо однорідне рівняння теплопровідності відповідає нагоди. відсутності джерел. Завдання Коші ставиться так: знайти функцію t), що задовольняє рівняння і початковій умові завдання Коші для рівняння теплопровідності Фізичний сенс завдання полягає у визначенні температури однорідного нескінченного стрижня в будь-який момент часу за відомою його температурі в момент часу. Вважається, що бокова поверхня стержня теплоізольована, так що через неї тепло з стрижня не йде. Припусти м, що досить гладкі функції, убиваююте при х2 + t2 + 00 настільки швидко, що сущ естве перетворення Фур'є 2) законні операції диференціювання Тоді, застосовуючи перетворення Фур'є до обох частин рівняння (1) і умові (2), від завдання (1 ) - (2) перейдемо до задачі Коші для звичайного диференціального рівняння (величина £ грає роль параметра). Рішення завдання (5) - (6) має вигляд Раніше ми встановили, що де перетворення Фур'є функції. Звідси, вважаючи t = отримуємо Таким чином, в правій частині рівності (7) варто твір перетворень Фур'є функцій Користуючись теоремою про згортку, в силу якої рівність (7) можна представити у вигляді Ліва частина формули (8) є перетворення Фур'є (по аргументу х ) шуканої функції і (х, t). так що формулу (8) можна переписати так: звідки, користуючись виразом для згортки функцій 4> (х) ие Л, маємо Отримана формула дає рішення вихідної задачі (1) - (2) і називається інтегралом Пуассона. Справді, можна довести, що для будь-якої неперервної і обмеженої функції ipt), яка визначається формулою (9), має похідні будь-якого порядку по х і по t при t> 0 і задовольняє рівняння (1) при t> 0 і Vx. Покажемо, що функція задовольняє початковій умові. Покладемо Тоді так що звідки при отримаємо так як Сформулюємо наступний важливий результат. Теорема 1. В класі обмежених функцій рішення задачі Кош і (1) - (2) єдино і безперервно залежить від початкової функції. Приклад. Знайти рішення задачі Коші Завдання Коші для рівняння теплопровідності А Користуючись формулою Пуассона (9), отримуємо прообразуя інтеграл в правій честі. Маємо Зробимо заміну змінної Тоді інтефал в правій частині останнього рівності набуде вигляду З формули (і) (Тут ми воспольеов опис тим, що отримуємо, що / Таким чином, рішення поставленого завдання про межу і ться формулою Лелю бачити, що побудований листопада функція u ( x, f) задовольняє початковій умові (2 '). Безпосередньою перевіркою легко переконатися в тому, що ата фуніція при задовольняє рівняння SautWtl. З формули Пуассона (9) випливає, що тепло расоросграня ється вздовж стрижня миттєво. Дійсно, нехай початкова температура) позитив на для і дорівнює нулю поза цим відрізком. Тоді для подальшого розподілу температур отримуємо звідки бачачи, що при як завгодно малих t> 0 і як завгодно великих | х | маємо tt (x, t)> 0. Це обьяс кяется неточністю теоретичних передумов при виводі рівняння теплопровідності. Не враховуючи юшіх інерціальна ость руху ня молекул. Проте, рівняння тепло про водності дає гарне кількісне узгодження з досвідом. Більш точний опис процесів переносу тепла дається так званими рівняннями переносу. 2.1. Фундаментальне рішення рівняння теплопровідності Функція входить в формулу Пуассона (9), називається фундаментальним рішенням рівняння теплопровідності. Вже згадана як функція аргументів х, t, вона задовольняє рівняння щ = а2іхх, в чому можна переконатися безпосередньою перевіркою. Фундаментальне рішення має важливе фізичний зміст, пов'язаний з поняттям теплового імпульсу. Припустимо, що початковий розподіл ip (x) температур таке: Тоді в силу (9) розподіл температур і, в стрижні матиме вигляд По теоремі про повну загальну середню де маємо Переходячи в останній рівності до межі при е - * 0, отримаємо Це означає, що функція G (x, t \ хо) представляє розподіл температур в стрижні в момент t> 0, якщо в початковий момент t = 0 в точці х = Хо був нескінченний пік температур (при е - * 0 функція 4> еt; xa) при в різних значеннях t> Оімеетвід (рис. 1). Криві 1, 2, 3 відповідають моментам часу • Малюнок показує, каквиравніва-ється температура в стрижні після теплового імпульсу. Рішення Завдання Коші для рівняння теплопровідності задачі теплопровідності в нескінченному стрижні при початковому умови можна розглядати як результат суперпозиції температур, що виникають в точці х в момент часу t внаслідок безперервно розподілених по стрижні теплових імпульсів інтенсивності у> (Л) в точці Л, прикладених в момент t = 0.