Визначення. Якщо функція f (x) визначена на відрізку [a, b], неперервна в кожній точці інтервалу (a, b), в точці a неперервна справа, в якій точці b неперервна зліва, то кажуть, що функція f (x) неперервна на відрізку [a, b].
Іншими словами, функція f (x) неперервна на відрізку [a, b], якщо виконані три умови:
Для функцій, безперервних на відрізку, розглянемо деякі властивості, які сформулюємо у вигляді наступних теорем, не проводячи доказів.
Теорема 1. Якщо функція f (x) неперервна на відрізку [a, b], то вона досягає на цьому відрізку свого найменшого і свого максимального значення.
Ця теорема стверджує (рис. 1.15), що на відрізку [a, b] знайдеться така точка x1. що f (x1) ≤ f (x) для будь-яких x з [a, b] і що знайдеться точка x2 (x2 [a, b]) така, що
Значення f (x1) є найбільшим для цієї функції на [a, b], а f (x2) - найменшим. Позначимо: f (x1) = M, f (x2) = m. Так як для f (x) виконується нерівність:. то отримуємо наступне наслідок з теореми 1.
Слідство. Якщо функція f (x) неперервна на відрізку, то вона обмежена на цьому відрізку.
Теорема 2. Якщо функція f (x) неперервна на відрізку [a, b] і на кінцях відрізка приймає значення різних знаків, то знайдеться така внутрішня точка x0 відрізка [a, b], в якій функція звертається в 0, тобто .
Ця теорема стверджує, що графік функції y = f (x), безперервної на відрізку [a, b], перетинає вісь Ox хоча б один раз, якщо значення f (a) і f (b) мають протилежні знаки. Так, (рис. 1.16) f (a)> 0, f (b) <0 и функция f(x) обращается в 0 в точках x1. x2. x3 .
Теорема 3. Нехай функція f (x) неперервна на відрізку [a, b], f (a) = A, f (b) = B і
A ≠ B. (рис. 1.17). Тоді для будь-якого числа C, укладеного між числами A та B, знайдеться така внутрішня точка x0 відрізка [a, b], що f (x0) = C.
Слідство. Якщо функція f (x) неперервна на відрізку [a, b], m - найменше значення f (x), M - найбільше значення функції f (x) на відрізку [a, b], то функція приймає (хоча б один раз) будь-яке значення m, укладену між m і M, а тому відрізок [m, M] є множиною всіх значень функції f (x) на відрізку [a, b].
Зауважимо, що якщо функція неперервна на інтервалі (a, b) або має на відрізку
[A, b] точки розриву, то теореми 1, 2, 3 для такої функції перестають бути вірними.
На закінчення розглянемо теорему про існування зворотної функції. Нагадаємо, що під проміжком розуміється відрізок або інтервал, або напівінтервал кінцевий або нескінченний.
Теорема 4. Нехай f (x) неперервна на проміжку X, зростає (або убуває) на X і має безліччю значень проміжок Y. Тоді для функції y = f (x) існує зворотна функція x = # 966; (y), певна на проміжку Y, безперервна і зростаюча (або спадна) на Y з безліччю значень X.
Зауваження. Нехай функція x = # 966; (y) є зворотною для функції f (x). Так як зазвичай аргумент позначають через x, а функцію через y, то запишемо зворотну функцію у вигляді y = # 966; (x).
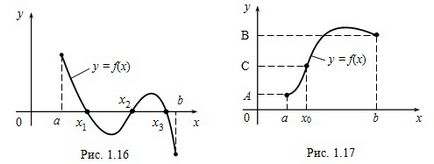
Приклад 1. Функція y = x 2 (рис. 1.8, а) на безлічі X = [0, + ∞) неперервна, зростає і має безліччю значень Y = [0, + ∞). Функція y = x 2 має зворотну функцію x = √y (рис. 1.8, б), а після переобозначеніе змінних y = √x. певну, безперервну і зростаючу на X.
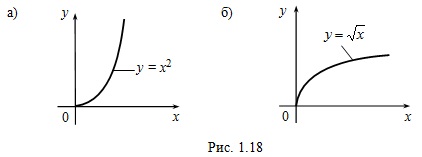
Приклад 2. Функція y = sinx (рис. 1.19, а) безперервна, зростає на відрізку і має безліччю значень відрізок [-1, 1], тому вона має зворотну функцію y = arcsinx (рис. 1.19, б), певну, безперервну і зростаючу на відрізку [-1, 1] і має безліч значень
Зауважимо, що графіки взаємно обернених функцій симетричні відносно прямої y = x. Пропонуємо побудувати графіки взаємно обернених функцій:
1. y = cosx, y = arccosx;
2. y = tgx, y = arctgx;
3. y = ctgx, y = arcctgx;
4. y = e x. y = lnx.