
Головна | Про нас | Зворотній зв'язок
В яких випадках в триангуляционной мережі виникає геометричне умова координат. Привести приклади.
Для того щоб при створенні геодезичної мережі можна було вирахувати на площині координати всіх знову визначаються пунктів, повинні бути відомі координати вихідного пункту, довжина і азимут вихідної сторони, а також необхідну кількість виміряних кутів або довжин сторін трикутників (в кожному трикутнику по два кута або по дві сторони). В цьому випадку координати пунктів визначаються однозначно, але безконтрольно, часом з великими помилками. При цьому не буде можливості ні виявити, ні усунути ці помилки, а також оцінити точність тих чи інших елементів мережі. Для усунення цих недоліків і підвищення точності побудови мережі, в ній виконують в досить великому обсязі так звані надлишкові вимірювання горизонтальних кутів, довжин сторін, азимутів сторін і т. П.
При вставці мережі нижчого класу в мережу більш високого класу крім надмірно виміряних кутів, довжин сторін і т. П. З'являються ще й надлишкові вихідні дані, які не підлягають змінам при зрівнянні вставляється мережі. До них відносяться координати пунктів, довжини і кути дирекцій сторін мережі більш високого класу.
При наявності в геодезичної мережі як надлишково виміряних величин, так і надлишкових вихідних даних виникає необхідність зрівнювання мережі за виникають в ній геометричні умови.
Умовні рівняння координат (абсцис і ординат) виникають тільки в тому випадку, якщо в мережі тріангуляції є роздільні групи вихідних (жорстких) пунктів, віддалені одна від одної не менше ніж на дві визначаються сторони. Окрема група вихідних пунктів може складатися або з одного такого пункту, або з декількох суміжних пунктів. Наприклад в одну групу вихідних пунктів входять два суміжних пункту А і В, а в іншу, віддалену від першої на дві визначаються сторони ВС і CD - один вихідний пункт D (рис. 1).
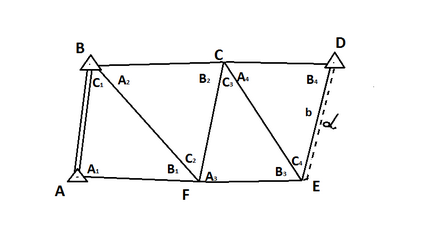
Мал. 1 Ланцюжок трикутників між трьома вихідними пунктами і виміряної
стороною і азимутом.
При складанні умов координат в мережі виділяють ланцюжок трикутників, що сполучає найближчі пункти різних груп вихідних пунктів, і в ній намічають ходову лінію, що проходить через вершини проміжних кутів трикутників.
У однаковох мережі повинні дотримуватися рівності:
XD = XB + Σ # 8710; x; yD = yB + Σ # 8710; y;
де # 8710; х 'і # 8710; у '- збільшення координат, обчислені з використанням виміряних кутів А', В ', С в трикутниках; ( # 8710; х), ( # 8710; у) - поправки в їх значення з зрівнювання мережі.
Для отримання умов координат в остаточному вигляді поправки ( # 8710; х) і ( # 8710; у) в прирости координат слід висловити через поправки (A), (В), (С) в виміряні кути в трикутниках. Виконавши ці перетворення, отримаємо для випадку зрівнювання тріангуляції по кутах:
умовне рівняння абсцис
Σ (хn - х) ctg А '(А) - Σ (хn - х) ctg В' (В) - Σ (yn - y) (± С) + 206,265 # 8060; X = 0;
Умовне рівняння ординат
Σ (yn - y) ctg А '(А) - Σ (yn - y) ctg В' (В) - Σ (xn - x) (± С) + 206,265 # 8060; y = 0;
У цих рівняннях: (хп-х) і (уп-у) - різниці координат (в км) останнього пункту D ходової лінії і координат поточних пунктів ходової лінії, включаючи вихідний пункт В на початку цієї лінії; (А) і (В) - поправки в сполучні кути A і В у трикутниках, при цьому вимірюється кут В лежить проти вихідної, а кут A- проти визначається в трикутнику сторони; (С) -поправкі в проміжні кути С, при цьому поправка (С) має знак плюс (+ С), якщо кут С розташований зліва від ходової лінії, і знаком мінус (-С), якщо праворуч від неї, йдучи від початкового пункту У цій лінії до кінцевого пункту D.
вільні члени # 8060; X і # 8060; y (в м) знаходять за формулами як різниці обчислених за вимірюються кутів координат хn ', yn' і заданих координат x, yконечного пункту D ходової лінії.
При зрівнюванні тріангуляції за напрямками поправки в кути висловлюють через поправки в виміряні напрямки.
Вивести формулу сферичного надлишку трикутника, використовуючи формулу Лежандра.
Після того як отримані остаточні значення виміряних напрямків або кутів на поверхні еліпсоїда, переходять до вирішення трикутників. Завдання полягає в послідовному обчисленні довжин сторін трикутників тріангуляції, причому відомі одна сторона і кути в кожному трикутнику.
Строго кажучи, трикутники тріангуляції є Сфероїдічеськая або еліпсоїдальної трикутниками, оскільки вони утворені на поверхні еліпсоїда. На практиці зазвичай доводиться мати справу з трикутниками, сторони яких не перевищують 40-50 км і в рідкісних випадках досягають 70-80 км. Внаслідок близькості земного еліпсоїда до сфери відмінність в елементах Сфероїдічеськая і сферичних трикутників тріангуляції занедбані. Таким чином, обчислення трикутників тріангуляції зводиться до вирішення сферичних трикутників. Якщо вирішувати трикутники за звичайними формулами сферичної тригонометрії, то сторони необхідно висловлювати в частинах радіуса, але це незручно, так як практично боку повинні бути виражені в метрах. Тому трикутники тріангуляції вирішують особливими методами, користуючись теоремою Лежандра або способом аддітаментов.
У сферичному трикутнику сума кутів більше 180 ° на величину, яка називається сферичним надлишком (# 603;).
Нехай АВС - сферичний трикутник, сторони якого в лінійних одиницях позначимо через a, b, с. По боках a, b, c побудуємо плоский трикутник А1, В1, С1, кути сферичного трикутника позначимо відповідно через А, В, С, а кути плоского - через А1, В1, С1
Шукані значення кутів плоского трикутника в остаточному вигляді виразяться простими формулами: А1 = А - # 603; / 3, В1 = В - # 603; / 3, С1 = С - # 603; / 3, де # 603; - сферичний надлишок трикутника. Ці формули виражають теорему Лежандра для малих трикутників.
Поставимо задачу знайти різниці кутів А-А1, В-В1, С-С1. Знаючи ці різниці, можемо від сферичних трикутників переходити до плоских, які мають такі ж значення довжин сторін, і таким чином, виробляти рішення трикутників, застосовуючи формули прямолінійною тригонометрії.
Позначимо через R радіус кулі, на якому побудований сферичний трикутник. Тоді, застосувавши формулу косинуса боку для сферичного трикутника АВС, напишемо:
Нехтуючи п'ятими ступенями малих величин. і формулу переписуємо у вигляді
З прийнятою точністю маємо
Після перемноження т приведення подібних членів отримаємо:
Для плоского трикутника А1У1С1 маємо
Беручи до уваги вирази (2) і (3), препісиваем формулу (1)
Різниця - мала величина, тому можна покласти:
На цій підставі отримуємо
Площа P трикутника може бути виражена формулою
Складаючи почленно три останніх рівняння і беручи до уваги, що
Так як сума кутів сферичного трикутника дорівнює 180º +. де - сферичний надлишок трикутника, то