У розглянутих раніше прикладах обчислювалися ймовірності елементарних подій. Виникає питання: як визначити ймовірність події, якщо відома якась інформація про події, що відбулися до нього? [1] Імовірність події А. при обчисленні якої враховується інформація про подію В. називається умовною і позначається як Р (А | В).
Імовірність події А за умови, що настав подія В. дорівнює ймовірності події А і В. поділеній на ймовірність події В:
Імовірність події В за умови, що настав подія А. дорівнює ймовірності події А і В. поділеній на ймовірність події А:
де Р (А і В) - ймовірність події А і В. Р (А) - ймовірність події А. Р (В) - ймовірність події В.
Завантажити замітку в форматі Word або pdf
Фактично формули (1) і (2) це короткий запис умовної ймовірності на основі таблиці спряженості ознак. Повернемося до прикладу, розглянутого в попередній замітці (рис. 1). Припустимо, що нам стало відомо, ніби якась сім'я збирається купити широкоекранний телевізор. Яка ймовірність того, що ця сім'я дійсно купить такий телевізор?

Мал. 1. Поведінка покупців широкоекранних телевізорів
В даному випадку нам необхідно обчислити умовну ймовірність Р (покупка здійснена | покупка планувалася). Оскільки нам відомо, що сім'я планує покупку, вибіркове простір складається не з усіх тисячі сімей, а тільки з тих, які планують покупку широкоекранного телевізора. З 250 таких сімей 200 дійсно купили цей телевізор. Отже, ймовірність того, що сім'я дійсно купить широкоекранний телевізор, якщо вона це запланувала, можна обчислити за такою формулою:
Р (покупка здійснена | покупка планувалася) = кількість сімей, які планували і купили великий телевізор / кількість сімей, які планували купити широкоекранний телевізор = 200/250 = 0,8
Цей же результат дає формула (2):
де подія А полягає в тому, що сім'я планує покупку широкоформатного телевізора, а подія В - в тому, що вона його дійсно купить. Підставляючи в формулу реальні дані, отримуємо:
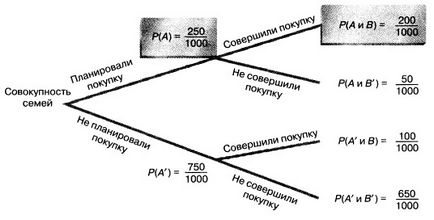
Мал. 2. Дерево рішень
Наприклад, щоб обчислити вірогідність того, що сім'я купить широкоекранний телевізор, якщо вона запланувала зробити це, слід визначити ймовірність події покупка запланована і здійснена. а потім поділити його на ймовірність події покупка запланована. Переміщаючись по дереву рішення, зображеному на рис. 2, отримуємо наступний (аналогічний попередньому) відповідь:
У прикладі з покупкою широкоекранного телевізора ймовірність того, що випадково обрана сім'я придбала великий телевізор за умови, що вона планувала це зробити, дорівнює 200/250 = 0,8. Нагадаємо, що безумовна ймовірність того, що випадково обрана сім'я придбала великий телевізор, дорівнює 300/1000 = 0,3. Звідси випливає дуже важливий висновок. Апріорна інформація про те, що сім'я планувала покупку, впливає на ймовірність самої покупки. Інакше кажучи, ці дві події залежать один від одного. На противагу цьому прикладу, існують статистично незалежні події, ймовірності яких не залежать один від одного. Статистична незалежність виражається тотожністю: Р (А | В) = Р (А). де Р (А | В) - ймовірність події А за умови, що відбулася подія В. Р (А) - безумовна ймовірність події А.
Зверніть увагу на те, що події А і В є статистично незалежними один від одного тоді і тільки тоді, коли Р (А | В) = Р (А). Якщо в таблиці спряженості ознак, що має розмір 2 × 2, ця умова виконується хоча б для однієї комбінації подій А і В. воно буде справедливим і для будь-якої іншої комбінації. У нашому прикладі події покупка запланована і покупка здійснена не є статистично незалежними, оскільки інформація про одну подію впливає на ймовірність іншого.
Розглянемо приклад, в якому показано, як перевірити статистичну незалежність двох подій. Запитаємо у 300 сімей, які купили широкоформатний телевізор, чи задоволені вони своєю покупкою (рис. 3). Визначте, чи пов'язані між собою ступінь задоволеності покупкою і тип телевізора.
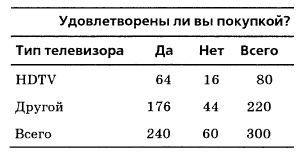
Мал. 3. Дані, що характеризують ступінь задоволеності покупців широкоекранних телевізорів
Судячи за цими даними,
Р (покупець задоволений) = 240/300 = 0,80
Отже, ймовірність того, що покупець задоволений покупкою, і того, що сім'я купила HDTV-телевізор, рівні між собою, і ці події є статистично незалежними, оскільки ніяк не пов'язані між собою.
Правило множення ймовірностей
Формула для обчислення умовної ймовірності дозволяє визначити ймовірність спільного події А і В. Дозволивши формулу (1)
щодо спільної ймовірності Р (А і В). отримуємо загальне, правило множення ймовірностей. Імовірність події А і В дорівнює ймовірності події А за умови, що настав подія В. помноженої на ймовірність події В:
(3) Р (А і В) = Р (А | В) * Р (В)
Розглянемо як приклад 80 сімей, які купили широкоекранний HDTV-телевізор (рис. 3). У таблиці вказано, що 64 сім'ї задоволені покупкою і 16 - немає. Припустимо, що серед них випадковим чином вибираються дві сім'ї. Визначте ймовірність, що обидва покупця виявляться задоволеними. Використовуючи формулу (3), отримуємо:
Р (А і В) = Р (А | В) * Р (В)
де подія А полягає в тому, що друга сім'я задоволена своєю покупкою, а подія В - в тому, що перша сім'я задоволена своєю покупкою. Імовірність того, що перша сім'я задоволена своєю покупкою, дорівнює 64/80. Однак імовірність того, що друга сім'я також задоволена своєю покупкою, залежить від відповіді першої сім'ї. Якщо перша сім'я після опитування не повертається до вибірки (вибір без повернення), кількість респондентів знижується до 79. Якщо перша сім'я опинилася задоволеною своєю покупкою, ймовірність того, що друга сім'я також буде задоволена, дорівнює 63/79, оскільки в вибірці залишилося тільки 63 сім'ї, задоволені своїм придбанням. Таким чином, підставляючи в формулу (3) конкретні дані, отримаємо таку відповідь:
Р (А і В) = (63/79) (64/80) = 0,638.
Отже, ймовірність того, що обидві родини задоволені своїми покупками, дорівнює 63,8%.
Припустимо, що після опитування перша сім'я повертається до вибірки. Визначте ймовірність того, що обидві родини виявляться задоволеними своєю покупкою. В цьому випадку ймовірності того, що обидві родини задоволені своєю покупкою однакові, і рівні 64/80. Отже, Р (А і В) = (64/80) (64/80) = 0,64. Таким чином, ймовірність того, що обидві родини задоволені своїми покупками, дорівнює 64,0%. Цей приклад показує, що вибір другої сім'ї не залежить від вибору першої. Таким чином, замінюючи у формулі (3) умовну ймовірність Р (А | В) ймовірністю Р (А). ми отримуємо формулу множення ймовірностей незалежних подій.
Правило множення ймовірностей незалежних подій. Якщо події А і В є статистично незалежними, ймовірність події А і В дорівнює ймовірності події А. помноженої на ймовірність події В.
Якщо це правило виконується для подій А і В. значить, вони є статистично незалежними. Таким чином, існують два способи визначити статистичну незалежність двох подій:
- Події А і В є статистично незалежними один від одного тоді і тільки тоді, коли Р (А | В) = Р (А).
- Події А і B є статистично незалежними один від одного тоді і тільки тоді, коли Р (А і В) = Р (А) Р (В).
Якщо в таблиці спряженості ознак, що має розмір 2 × 2, одна з цих умов виконується хоча б для однієї комбінації подій А і B. воно буде справедливим і для будь-якої іншої комбінації.
Безумовна вірогідність елементарного події
де події B1. B2. ... Bk є взаємовиключними і вичерпними.
Проілюструємо застосування цієї формули на прикладі рис.1. Використовуючи формулу (5), отримуємо:
де Р (А) - ймовірність того, що покупка планувалася, Р (В1) - ймовірність того, що покупка здійснена, Р (В2) - ймовірність того, що покупка не здійснена.
Умовна ймовірність події враховує інформацію про те, що сталося якесь інше подія. Цей підхід можна використовувати як для уточнення ймовірності з урахуванням знову надійшла інформації, так і для обчислення ймовірності, що спостережуваний ефект є наслідком якоїсь конкретної причини. Процедура уточнення цих ймовірностей називається теоремою Байеса. Вперше вона була розроблена Томасом Байєса в 18 столітті.
Припустимо, що компанія, згадана вище, досліджує ринок збуту нової моделі телевізора. У минулому 40% телевізорів, створених компанією, користувалися успіхом, а 60% моделей визнання не отримали. Перш ніж оголосити про випуск нової моделі, фахівці з маркетингу ретельно досліджують ринок і фіксують попит. У минулому успіх 80% моделей, які отримали визнання, прогнозувався заздалегідь, в той же час 30% сприятливих прогнозів виявилися невірними. Для нової моделі відділ маркетингу дав сприятливий прогноз. Яка ймовірність того, що нова модель телевізора буде користуватися попитом?
Теорему Байеса можна вивести з визначень умовної ймовірності (1) і (2). Щоб обчислити вірогідність Р (В | А), візьмемо формулу (2):
і підставимо замість Р (А і В) значення з формули (3):
Р (А і В) = Р (А | В) * Р (В)
Підставляючи замість Р (А) формулу (5), отримуємо теорему Байеса:
де події B1. В 2. ... Вk є взаємовиключними і вичерпними.
Введемо наступні позначення: подія S - телевізор користується попитом. подія S '- телевізор не користується попитом. подія F - сприятливий прогноз. подія F '- несприятливий прогноз. Припустимо, що P (S) = 0,4, P (S ') = 0,6, P (F | S) = 0,8, P (F | S') = 0,3. Застосовуючи теорему Байеса отримуємо:
Імовірність попиту на нову модель телевізора за умови сприятливого прогнозу дорівнює 0,64. Таким чином, ймовірність відсутності попиту за умови сприятливого прогнозу дорівнює 1-0,64 = 0,36. Процес обчислень представлений на рис. 4.

Мал. 4. (а) Обчислення за формулою Байеса для оцінки ймовірності попиту телевізорів; (Б) Дерево рішення при дослідженні попиту на нову модель телевізора
Розглянемо приклад застосування теореми Байєса для медичної діагностики. Імовірність того, що людина страждає від певного захворювання, дорівнює 0,03. Медичний тест дозволяє перевірити, чи так це. Якщо людина дійсно хвора, ймовірність точного діагнозу (який стверджує, що людина хвора, коли він дійсно хворий) дорівнює 0,9. Якщо людина здорова, ймовірність ложноположительного діагнозу (який стверджує, що людина хвора, коли вона здорова) дорівнює 0,02. Припустимо, що медичний тест дав позитивний результат. Яка ймовірність того, що людина дійсно хвора? Яка ймовірність точного діагнозу?
Введемо наступні позначення: подія D - людина хвора. подія D '- людина здорова. подія Т - діагноз позитивний. подія Т '- діагноз негативний. З умови задачі випливає, що Р (D) = 0,03, P (D ') = 0,97, Р (T | D) = 0,90, P (T | D') = 0,02. Застосовуючи формулу (6), отримуємо:
Імовірність того, що при позитивному діагнозі людина дійсно хвора, дорівнює 0,582 (див. Також рис. 5). Зверніть увагу на те, що знаменник формули Байеса дорівнює ймовірності позитивного діагнозу, тобто 0,0464.
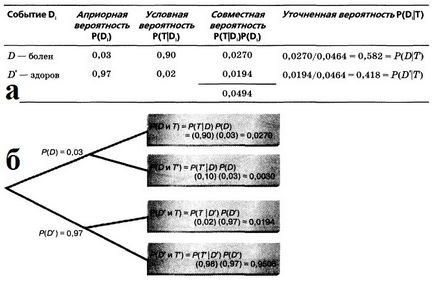
Мал. 5. (а) Обчислення за формулою Байеса для оцінки точності медичного діагнозу; (Б) Дерево рішення при оцінці точності медичного діагнозу
Можливо, вас також зацікавить: