Доведемо, що $ MN || AD \ і \ MN = \ frac $.
Розглянемо вектор $ \ overrightarrow $. Використовуємо далі правило багатокутника для додавання векторів. З одного боку отримаємо, що
З іншого боку
Складемо два останніх рівності, отримаємо
Так як $ M $ і $ N $ - середини бічних сторін трапеції, то матимемо
З цього ж рівності (так як $ \ overrightarrow $ і $ \ overrightarrow $ сонаправлени, а, отже, колінеарні) отримуємо, що $ MN || AD $.
Приклади завдань на поняття середньої лінії трапеції
Бічні сторони трапеції рівні $ 15 \ см $ і $ 17 \ см $ відповідно. Периметр трапеції дорівнює $ 52 \ см $. Знайти довжину середньої лінії трапеції.
Позначимо середню лінію трапеції через $ n $.
Сума бічних сторін дорівнює
\ [15 \ см + 17 \ см = 32 \ см \]
Отже, так як периметр дорівнює $ 52 \ см $, сума підстав дорівнює
\ [52 \ см-32 \ см = 20 \ см \]
Значить, по теоремі 1, отримуємо
Кінці діаметра окружності віддалені від його дотичній відповідно на $ 9 $ см і $ 5 $ см. Знайти діаметр цього кола.
Нехай нам дана окружність з центром в точці $ O $ і діаметром $ AB $. Проведемо дотичну $ l $ і побудуємо відстані $ AD = 9 \ см $ і $ BC = 5 \ см $. Проведемо радіус $ OH $ (рис. 2).
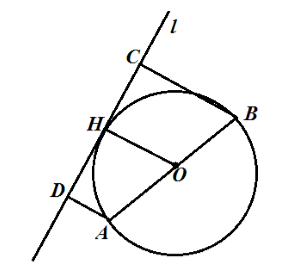
Так як $ AD $ і $ BC $ - відстані до дотичній, то $ AD \ bot l $ і $ BC \ bot l $ і так як $ OH $ - радіус, то $ OH \ bot l $, отже, $ OH | \ left | AD \ right || BC $. З цього всього отримуємо, що $ ABCD $ - трапеція, а $ OH $ - її середня лінія. По теоремі 1, отримуємо
\ [D = 2OH = 2 \ cdot 7 \ см = 14 \ см. \]