Загальний вигляд одночлена
-a - коефіцієнт, який може належати будь-якій з множин N, Z, Q, R, C
-n показник ступеня, який належить множині N
Два одночлена подібні, якщо вони мають одну і ту ж змінну і однаковий показник ступеня.
Приклади: 3x 2 і -5x 2; ½x 4 і 2√3x 4
Сума одночленним, що не подібних один одному, називається многочленом (або поліномом). В цьому випадку одночлени є складовою частиною полінома. Поліном, що містить два доданків, називається біном (або Двочленні).
Приклад: p (x) = 3x 2 -5; h (x) = 5x-1
Поліном, що містить три доданків, називається тричленної.
p (x) = an x n + an-1 x n-1 +. + A1 x 1 + a0
де:
- an, an-1, an-2. a1, a0 - коефіцієнти полінома. Вони можуть бути натуральними, цілими, раціональними, дійсними або комплексними числами.
- an - коефіцієнт при слагаемом з найбільшим показником ступеня (провідний коефіцієнт)
- a0 - коефіцієнт при слагаемом з найменшим показником ступеня (вільний член, або константа)
- n - ступінь полінома
p (x) = 5x 3 -2x 2 + 7x-1
- поліном третього ступеня з коефіцієнтами 5, -2, 7 і -1
- 5 - провідний коефіцієнт
- -1 - вільний член
- x - змінна
h (x) = - 2√3x 4 + ½x-4
- поліном четвертого ступеня з коефіцієнтами -2√3, ½ і -4
- -2√3 - провідний коефіцієнт
- -4 - вільний член
- x - змінна
розподіл полиномов
Щоб знайти приватне і залишок від ділення p (x) на q (x). потрібно використовувати наступний алгоритм:- Ступінь p (x) повинна бути більше або рівній мірі q (x).
- Ми повинні записати обидва полінома в порядку зниження ступеня. Якщо в p (x) немає члена з якою-небудь мірою, його треба дописати з коефіцієнтом 0.
- Ведучий член p (x) ділиться на провідний член q (x). і результат записується під розділової лінією (в знаменнику).
- Множимо отриманий результат на всі члени q (x) і записуємо результат з протилежними знаками під членами p (x) з відповідними ступенями.
- Складаємо почленно доданки з однаковими ступенями.
- До результату приписуємо залишилися члени p (x).
- Ділимо провідний член отриманого полінома на перший член полінома q (x) і повторюємо кроки 3-6.
- Ця процедура повторюється до тих пір, поки знову отриманий поліном не матиме меншу ступінь, ніж q (x). Цей поліном буде залишком від ділення.
- Поліном, записаний під розділової лінією, є результатом поділу (приватним).
приклад 1
Крок 1 і 2) $ p (x) = x ^ 5-3x ^ 4 + 2x ^ 3 + 7x ^ 2-3x + 5 \\ q (x) = x ^ 2x + 1 $
3) x 5 -3x 4 + 2x 3 + 7x 2 -3x + 5
Відповідь: x 4 + 3x 2 + 2x - 8 = (x 2 - 3x) (x 2 + 3x + 12) + 38x - 8
Розподіл на поліном першого ступеня
Цей поділ можна виконати з використанням вищезгаданого алгоритму або навіть більш швидким чином, якщо скористатися методом Горнера.
Якщо f (x) = an x n + an-1 x n-1 +. + A1 x + a0. поліном можна переписати у вигляді f (x) = a0 + x (a1 + x (a2 +. + x (an-1 + an x).))
q (x) - поліном першого ступеня → q (x) = mx + n
Тоді поліном в приватному матиме ступінь n-1.
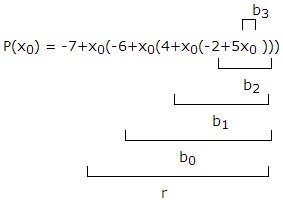
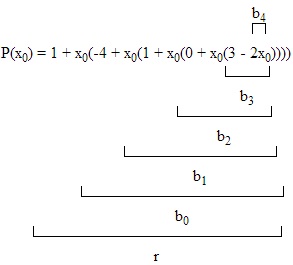
приклад 5
p (x) = 3x 3 -5x 2 + 2x + 3
q (x) = 2x-1
$ X_0 = \ frac $
p (x) = 3 + x (2 + x (-5 + 3x))
b2 = 3
$ B_1 = \ frac \ cdot 3-5 = - \ frac $
$ B_0 = \ frac \ cdot \ left (- \ frac \ right) +2 = - \ frac + 2 = \ frac $
$ R = \ frac \ cdot \ frac + 3 = \ frac + 3 = \ frac \ Rightarrow c (x) = 3x ^ 2 \ fracx + \ frac $
$ \ Rightarrow 3x ^ 3-5x ^ 2 + 2x + 3 = (2x-1) (3x ^ 2 - \ fracx + \ frac) + \ frac $
висновок
Якщо ми ділимо на поліном ступеня вище, ніж один, для знаходження приватного та залишку потрібно скористатися алгоритмом 1-9.
Якщо ми ділимо на поліном першого ступеня mx + n. то для знаходження приватного та залишку потрібно використовувати метод Горнера з $ x_0 = - \ frac $.
Якщо нас цікавить тільки залишок від ділення, досить знайти p (x0).
приклад 6
p (x) = - 4x 4 + 3x 3 + 5x 2 -x + 2
q (x) = x-1
x0 = 1
r = p (1) = - 4.1 + 3.1 + 5.1-1 + 2 = 5
r = 5