З наших лекцій
Нехай у нас є інтервал (a. B), в якому ми точно знаємо, що функція f (x) має екстремум і він 1. А так же функція унімодальне і диференційована.
Метод Ньютона - це один з методів з використанням похідних. По суті метод Ньютона повторює той же метод дотичних, тільки застосовується до перших похідних.
Побудуємо функцію f (x) на інтервалі (a. B)
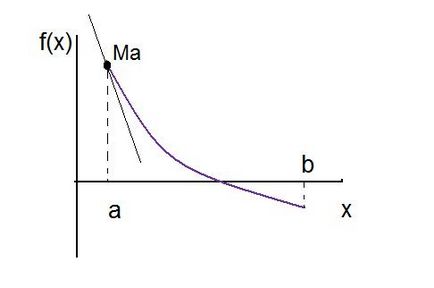
Розкладемо похідну функції в ряд Тейлора в точці (x 0, f '(x 0)):
Апроксимуємо. взявши тільки перші 2 доданків з ряду:
Звідси отримуємо, що
Таким чином, можна написати рекуррентное вираз:
Цей метод можна застосовувати тільки якщо функція двічі диференційована.
Якщо на відрізку [a. b] 3я похідна зберігає знак, то:
Володіє квадратической сходимостью (це найвища збіжність), якщо виконується умова збіжності.
Немає глобальної збіжності (тобто збіжність залежить від вибору початкової точки)
На кожному кроці методу необхідно обчислювати 1ю і 2ю похідні.
З інтернету (докладно + док-ва + модифікації):
Евристичні міркування, що призводять до методу Ньютона безумовної оптимізації.
Якщо виходити з того, що необхідним етапом знаходження рішення задачі
Геометрична інтерпретація формул (3) і (4) наведена на рис. 10а і 10б.
Метод Ньютона відноситься до методів другого порядку. оскільки для обчислення кожної ітерації потрібне знання другої похідної функції f. З тих же міркувань градієнтний метод відносять до методів першого порядку. Підкреслимо, що тут мова йде не про порядок збіжності методу, а про порядок використовуваних методом похідних функції, що мінімізується.
Теорема про локальнойсверхлінейнойсходімості методу Ньютона.
Нехай f двічі неперервно диференційовна, а x * -невирожденная стаціонарна точка. Тоді знайдеться околиця V x * точки x * така, що наближення (4). розпочаті з довільної початкової точкіx 0 ∈ V x *. сверхлінейносходятся
Доведення. Очевидно, F = f '∈ C 1 і тому
Оскільки F '(x *) невирождени. в силу (7) при x достатньо близьких до x * невирождени і оператор F '(x) і більш того,
Тому, зокрема, при x достатньо близьких до x *
Далі, в силу того, що F дифференцируема, а x * - стаціонарна точка,
x - x * - [F '(x)] -1 F (x) = [F' (x)] -1 F '(x) (x - x *) - [F' (x)] -1 F (x) =
= [F '(x)] -1 [F' (x) (x - x *) - F (x)] = o (x - x *).
x n +1 - x * = x n - [F '(x n)] -1 F (x n) - x * # 8797;
# 8797; # 966; (x n - x *) = o (x n - x *).
і, отже, x n → x * при n → ∞. Більш того, для довільного q ∈ (0, 1) знайдеться # 949;> 0 таке, що || # 968; (x - x *) || ≤ q || x - x * || при || x - x * || ≤ # 949 ;. Але тоді, якщо || x n - x * || ≤ # 949;, то || x n +1 - x * || ≤ q || x n - x * ||. З останнього твердження очевидним чином випливає потрібне співвідношення || x n - x * || ≤ Cq n.
Зрозуміло, як метод другого порядку. метод Ньютона вимагає більшого обсягу обчислювальної роботи, оскільки доводиться обчислювати другі похідні функції f.
Якщо функція f додатково сильно опукла. то можна стверджувати збіжність саме до вирішення завдання (1). а не тільки до стаціонарної точки функції f. і, крім того, оцінити радіус околиці, з якої наближення Ньютона сходяться.
Теорема про квадратичної збіжності методу Ньютона.
Нехай f ∈ C 2 і, більш того, f '' задовольняє умові Ліпшиця з константою L. Нехай f сильно випуклас константою # 955 ;. Нехай V x * - околиця рішення задачі (1). що складається з точок x ∈ Rm таких, що
У деяких завданнях більш істотним недоліком методу Ньютона є його велика обчислювальна складність: на кожному кроці потрібно обчислення оператора (матриці) f '' (x n) і його (її) звернення, що при великих размерностях ст óит в обчислювальному плані дуже дорого. Один із способів обходу цих труднощів полягає в "заморожуванні" оператора f '' (x n) - використання на кожному кроці [f '' (x 0)] -1 замість [f '' (x n)] -1:
Геометрична інтерпретація модифікованого методу Ньютона (14) зображена на рис. 12.
Можна показати, що при природних обмеженнях модифікований метод Ньютона сходиться лише лінійно (це плата за зменшення обсягу обчислень). Можна також Не заморожувати оператор [f '' (x n)] -1 назавжди, а оновлювати його через кілька етапів, скажімо k: