> Квадратурной формули обчислені за формулою (3), то відповідну квадратурну формулу називають квадратурної формулою интерполяционного типу.
> Квадратурной формули (2) при заданому розташуванні вузлів
не залежить від виду підінтегральної функції.
2. У квадратурних формулах интерполяционного типу залишковий член Rn [f] може бути представлений у вигляді значення конкретного диференціального оператора на функції f (x). для
.
3. Для поліномів до порядку n включно квадратурная формула (2) точна, тобто
. Найвищий ступінь полінома, для якого квадратурная формула точна, називається ступенем квадратурной формули.
Розглянемо окремі випадки формул (2) і (3): метод прямокутників, трапецій, парабол (метод Сімпсона). Назви цих методів обумовлені геометричній інтерпретацією відповідних формул.
Певний інтеграл функції від функції f (x):
чисельно дорівнює площі криволінійної трапеції, обмеженої кривими у = 0, x = a, x = b, y = f (x) (рисунок. 1).
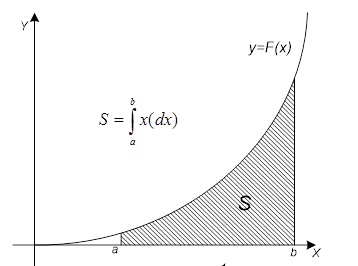
Мал. 1 Площа під кривою y = f (x) Для обчислення цієї площі весь інтервал інтегрування [a, b] розбивається на n рівних підінтервалів довжини h = (b-a) / n. Площа під підінтегральної кривої наближено замінюється на суму площ прямокутників, як це показано на малюнку (2).
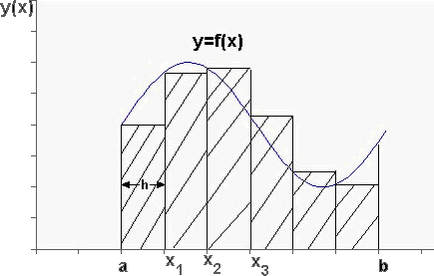
Мал. 2 Площа під кривою y = f (x) апроксимується сумою площ прямокутників
Сума площ всіх прямокутників обчислюється за формулою
Метод, представлений формулою (4), називається методом лівих прямокутників, а метод, представлений формулою (5) - методом правих прямокутників:
Похибка обчислення інтеграла визначається величиною кроку інтегрування h. Чим менше крок інтегрування, тим точніше інтегральна сума S аппроксимирует значення інтеграла I. Виходячи з цього будується алгоритм для обчислення інтеграла із заданою точністю. Вважається, що інтегральна сума S представляє значення інтеграла I c точністю eps, якщо різниця по абсолютній величині між інтегральними сумами
, обчисленими з кроком h і h / 2 відповідно, не перевищує eps.
Метод середніх прямокутників
Для знаходження визначеного інтеграла методом середніх прямокутників площа, обмежена прямими a і b, розбивається на n прямокутників з підставами h, висотами прямокутників будуть точки перетину функції f (x) з центрами прямокутників (h / 2). Інтеграл буде чисельно дорівнює сумі площ n прямокутників (рисунок 3).
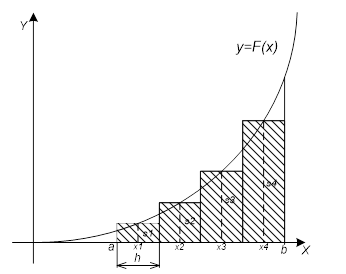
Мал. 3 Площа під кривою y = f (x) апроксимується сумою площ прямокутників
,
n - кількість розбиттів відрізка [a, b].
Для знаходження визначеного інтеграла методом трапецій площа криволінійної трапеції також розбивається на n прямокутних трапецій з висотами h і підставами в1. у2. у3. уn. де n - номер прямокутної трапеції. Інтеграл буде чисельно дорівнює сумі площ прямокутних трапецій (рисунок 4).
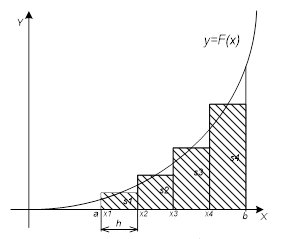
Мал. 4 Площа під кривою y = f (x) апроксимується сумою площ прямокутних трапецій.
n - кількість розбиттів
Похибка формули трапецій оцінюється числом
Похибка формули трапецій з ростом
зменшується швидше, ніж похибка формули прямокутників. Отже, формула трапецій дозволяє отримати більшу точність, ніж метод прямокутників.
Якщо для кожної пари відрізків
побудувати многочлен другого ступеня, потім проінтегрувати його на відрізку
і скористатися властивістю адитивності інтеграла, то отримаємо формулу Сімпсона.
У методі Сімпсона для обчислення певного інтеграла весь інтервал інтегрування [a, b] розбивається на підінтервали рівної довжини h = (b-a) / n. Число відрізків розбиття є парним числом. Потім на кожній парі сусідніх підінтервалів подинтегральная функція f (x) замінюється многочленом Лагранжа другого ступеня (малюнок 5).
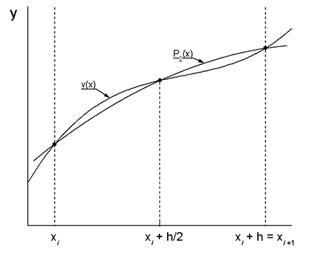
Мал. 5 Функція y = f (x) на відрізку
замінюється многочленом 2-го порядку
Розглянемо підінтегральної функції
. Замінимо цю підінтегральної функції інтерполяційним многочленом Лагранжа другого ступеня, що збігається з y =
:
.:
Введемо заміну змінних:
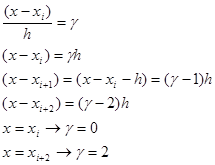
З огляду на формули заміни,
Виконавши інтегрування, отримаємо формулу Сімпсона:
Отримане для інтеграла
значення збігається з площею криволінійної трапеції, обмеженою віссю
,
і параболою, що проходить через точки
формула Сімпсона матиме вигляд:
У формулі параболи значення функції f (x) в непарних точках розбиття х1. х3. х2n-1 має коефіцієнт 4, в парних точках х2. х4. х2n-2 - коефіцієнт 2 і в двох граничних точках х0 = а, хn = b - коефіцієнт 1.
Геометричний сенс формули Сімпсона: площа криволінійної трапеції під графіком функції f (x) на відрізку [a, b] наближено замінюється сумою площ фігур, що лежать під параболами.
Якщо функція f (x) має на [a, b] безперервну похідну четвертого порядку, то абсолютна величина похибки формули Сімпсона але лише
де М - найбільше значення
на відрізку [a, b]. Так як n 4 зростає швидше, ніж n 2. то похибка формули Сімпсона з ростом n зменшується значно швидше, ніж похибка формули трапецій.
Цей інтеграл легко обчислюється:
Візьмемо n рівним 10, h = 0.1, розрахуємо значення підінтегральної функції
в точках розбиття
, а також напівцілий точках
.
За формулою середніх прямокутників отримаємо Iпрям = 0.785606 (похибка дорівнює 0.027%), за формулою трапецій Iтрап = 0.784981 (похибка близько 0,054. При використанні методу правих і лівих прямокутників похибка становить понад 3%.
Для порівняння точності наближених формул обчислимо ще раз інтеграл
,
але тепер за формулою Сімпсона при n = 4. Розіб'ємо відрізок [0, 1] на чотири рівні частини точками х0 = 0, х1 = 1/4, х2 = 1/2, х3 = 3/4, х4 = 1 і обчислимо наближено значення функції f (x) = 1 / ( 1 + x) в цих точках: у0 = 1,0000, у1 = 0,8000, у2 = 0,6667, у3 = 0,5714, у4 = 0,5000.
За формулою Сімпсона отримуємо
Оцінимо похибка отриманого результату. Для підінтегральної функції f (x) = 1 / (1 + x) маємо: f (4) (x) = 24 / (1 + x) 5. звідки випливає, що на відрізку [0, 1]
. Отже, можна взяти М = 24, і похибка результату не перевищує величини 24 / (2880 × 4 4) = 0.0004. Порівнюючи наближене значення з точним, укладаємо, що абсолютна помилка результату, отриманого за формулою Сімпсона, менше 0,00011. Це знаходиться у відповідності з цією вище оцінкою похибки і, крім того, свідчить, що формула Сімпсона значно точніше формули трапецій. Тому формулу Сімпсона для наближеного обчислення визначених інтегралів використовують частіше, ніж формулу трапецій.
Порівняння методів по точності
Порівняємо методи по точності, для цього зробимо обчислення інтеграла функцій y = x, y = x + 2, y = x 2. при n = 10 і n = 60, a = 0, b = 10. Точне значення інтегралів становить відповідно: 50, 70, 333. (3)
З таблиці 1 видно, що найбільш точним є інтеграл, знайдений за формулою Сімпсона, при обчисленні лінійних функцій y = x, y = x + 2 також досягається точність методами середніх прямокутників і методом трапецій, метод правих прямокутників є менш точним. З таблиці 1 видно, що при збільшенні кількості розбиттів n (збільшення числа інтеграцій) підвищується точність наближеного обчислення інтегралів
Завдання на лабораторну роботу
1) Написати програми обчислення певного інтеграла методами: середніх, правих прямокутників, трапеції і методом Сімпсона. Виконати інтегрування таких функцій:
на відрізку [0, 1] з кроком
,
,
3. Виконати варіант індивідуального завдання (таблиця 2)
Таблиця 2 Індивідуальні варіанти завдання