Визначення 7. Якщо рівність (8.1) здійснимо лише при всіх, то вектори а1. А2. акназиваютсялінейно незалежними.
Визначення 8. Якщо має місце рівність, то кажуть, що вектор b являетсялінейной комбінацією векторів а1. А2. ак. ілілінейновиражается через ці вектори.
Зауважимо, що якщо вектори а1. А2. ак лінійно залежні, то тоді, принаймні, один з векторів може бути лінійно виражений через інші. Це випливає з самого визначення 6, так як, якщо хоча б один з, то на нього можна виконати поділ інших і тоді будемо мати, де. Вірно і зворотне твердження, що якщо один з векторів лінійно виражається через інші, то всі ці вектори в сукупності лінійно залежні.
Зауважимо, що якщо вектори a і b НЕ колінеарні або a. b і c НЕ компланарність. то такі вектори є лінійно незалежними відповідно на площині або в просторі.
Покажемо це на прикладі трьох некомпланарних векторів a. b і c. Доказ проведемо методом від противного, припустивши, що зазначені вектори хоча і не компланарність. але лінійно залежні. Тоді має виконуватися умова лінійної залежності векторів, тобто і нехай при цьому. Тоді на можна розділити ліву і праву частину рівняння і в результаті матимемо вираз, яке суперечить визначенню 10 ( ""), тобто хоча вектори a. b і c НЕ компланарність. але вектор a лінійно виражається через два інших b і c. що говорить (за визначенням 8) про їх лінійної залежності. З цього випливає, що вектор a повинен бути лінійно незалежний з векторами b і c. Цікаво, що в тривимірному просторі будь-які чотири просторових вектора будуть лінійно залежними.
Два ненульових вектора a і b ортогональні. якщо вони перпендикулярні (проекція вектора a на b і проекція вектора b на a дорівнюють нулю). Тоді записують. Такі вектори завжди лінійно незалежні.
Якщо ненульові вектори a. b і c попарно ортогональні, то тоді вони утворюють трійку лінійно незалежних векторів.
Визначення 9. Рангомсістеми векторів називається максимальна кількість її лінійно незалежних векторів.
Визначення 10. Лінійне простір називається n -мірним. якщо в ньому можна знайти n лінійно незалежних векторів, а будь-яка система, що складається з більшої кількості векторів, є лінійно залежною в цьому просторі.
Наприклад, вектори, що лежать на одній прямій. утворюють одномірний простір. в якому тільки один незалежний вектор. а всі інші можуть бути виражені лінійними співвідношеннями через нього. На площині безліч векторів утворює двовимірне простір. тобто в цьому просторі визначені тільки два незалежних вектора.
Визначення 11. Якщо простір має кінцеве безліч лінійно незалежних векторів, то його називаютконечномерним. а якщо в ньому можна знайти скільки завгодно багато лінійно незалежних векторів, то - безкінечномірні.
Визначення 12. Сукупність n лінійно незалежних одиничних векторів n мірного простору називаютбазісом n мірного простору.
Зауважимо, що через базисні вектори можуть бути виражені будь-які інші вектори, які визначаються в даному базисі.
Теорема. Кожен вектор х лінійного n мірного простору можна представити, і до того ж єдиним чином, у вигляді лінійної комбінації векторів базису.
Доказ теореми складається з двох частин. Спочатку ми доведемо можливість висловити будь-який довільний вектор через базис лінійного простору. а потім, що розкладання довільного вектора з даного базису єдине.
Нехай довільний базис n мірного простору R і деякий довільний вектор. Так як кожні n + 1 векторів n мірного простору R лінійно залежні (визначення 6), то система, яку утворюють вектори l1. l2. ln і x повинна бути лінійно залежною. А це означає, що виконується рівність
де - числа одночасно не рівні нулю. При цьому ясно, що, так як в противному випадку хоча б одне з чисел не було подібне б нулю і тоді рівність (8.2) мало б вигляд
що в свою чергу. показувало б лінійну залежність базисних векторів. Висловимо x з рівності (8.2), розділивши на коефіцієнти при li і перенісши їх в праву частину. Після виконання зазначених перетворень маємо
Доведемо тепер, що розкладання (8.4) вектора x з даного базису l1. l2. ln єдине. Припустимо, що вектор x в просторі R має два різних розкладання
Тоді віднімемо з одного рівності інше, і так як в лівих частинах рівності стоїть один і той же вектор. то отримаємо
отже, маємо систему
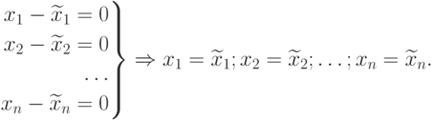
Останній вираз повністю доводить теорему.