Це означає, що нескінченні множини A і b еквівалентні, A̴B. мають «однакову потужність». Цікаво, що при цьому множествоA еквівалентно своєму подмножествуB, A
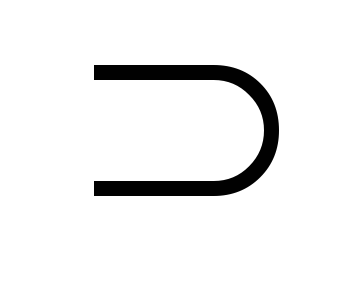
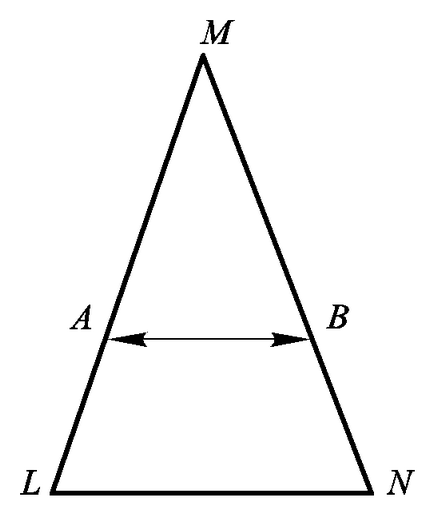
Мал. 7.6. Встановлення взаємно однозначної відповідності між рівними сторонами рівнобедреного трикутника.
2. ПустьLM іNM- рівні сторони рівнобедреного треугольнікаLMN (рис. 7.6).
Зв'язавши точки А верб рівних сторін трикутника відрізками прямих, паралельних основаніюLN. отримаємо взаємно однозначна відповідність між точками множин, що визначаються отрезкаміLM іNM. Отже, ці безлічі еквівалентні і мають однакову потужність.
3. Нехай тепер LN і МN - нерівні сторони трикутника LMN (рис. 7.7). Зв'язавши точки А і В на цих сторонах відрізками прямих, паралельних стороні LM. отримаємо, що і нерівні між собою сторони визначають безлічі точок однакової потужності. Справа в
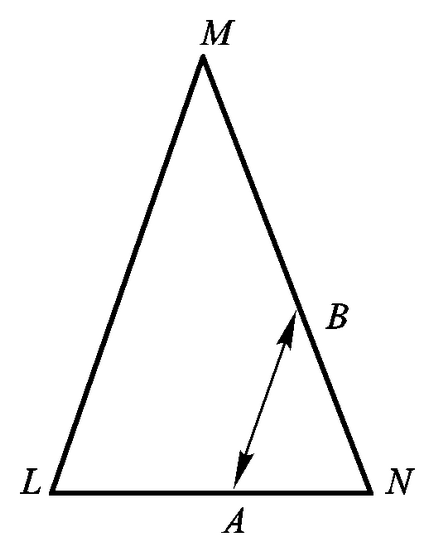
Мал. 7.7. Встановлення взаємно однозначної відповідності між нерівними сторонами рівнобедреного трикутника.
тому, що сторониLN іMN мають різну довжину, але кожна з них містить безліч точок, яких однаково "багато".
рахункові безлічі
Безліч назвемо Рахункової. якщо воно еквівалентно безлічі натуральних чисел.
Таким чином, можливість «пронумерувати» всі елементи множини визначає його счетності. Це завдання далеко не завжди вирішується просто.
Відзначимо деякі властивості рахункових множин.
1. З будь-якого нескінченної кількості завжди можна виділити рахункове безліч.
Дійсно, якщо множина A нескінченно, то рахункове множествоN можна побудувати наступним чином. Виділимо в якості першого елемента множестваN, наприклад, елементмножестваA .Так какA нескінченно, то виключення з нього одного елементасохраніт його нескінченність. Далі відділимо від залишився безлічі елемент, приєднавши його до безлічі N. потім з нескінченної кількості відділимо елемент, приєднавши егокN, і так далі. МножествоN набуде вигляду: і буде рахунковим.
Наведіть приклад, який ілюструє це властивість.
2. Будь-яке нескінченна підмножина рахункового безлічі теж лічильно.
Якщо множина A лічильно, а B- його нескінченна підмножина, то, перебираючи послідовно елементи множини A. ми будемо зустрічати елементи множини B і, нумеруя їх, тобто елементи множини B. B

3. Об'єднання будь-якого кінцевого або рахункового безлічі рахункових множин є рахункове безліч.
Для доказу цього властивості розглянемо рахункові безлічі:
Сформуємо з цих множин нове безліч
Воно утворюється так, що спочатку розташовується елемент, потім йдуть елементи, у яких сума індексів равна3. потом4. і так далі. Таке безліч охоплює всі елементи безлічі саме є рахунковим, еквівалентнимN.
потужність континууму
Розглядаючи властивості рахункових множин, ми прагнули довести счетності тих чи інших нескінченних множин. Однак чи всі нескінченні множини Рахункової? Щоб виявити незліченні безлічі, довелося подолати чимало труднощів. І Б. Больцано, і Г. Кантор, відчуваючи, що ідея встановлення взаємно однозначної відповідності є ключ до пошуку потужності нескінченних множин, були близькі до вирішення питання одночасно. Б. Больцано першим прийшов до способу оцінки нескінченних множин шляхом встановлення взаємно однозначної відповідності, а Г. Кантор першим зумів знайти незліченну безліч. Воно нескінченно і не еквівалентно безлічі натуральних чисел.
ТЕОРЕМА. Відрізок числової прямої містить незліченну безліч точок.
(Інший спосіб доведення цієї теореми, «діагональний метод Кантора», наведено в додатку)
Припустимо гидке: - рахункове безліч точок. Пронумеруємо їх:
Будь-яка точка цього відрізка виявляється включеною в цю послідовність?
Для доведення теореми слід знайти таку точку на відрізку, яка не охоплюється даної послідовністю.
Для цього розділимо відрізок на три рівні частини (рис. 7.8). Отримаємо відрізки:
Мал. 7.8. Побудова точки, яка не входить в послідовність.
Чому ділимо на 3 частини, а не навпіл або ж на 4 частини? Чому ці 3 частини повинні бути рівні?
Хоча б на одному з них немає точки. Виділивши його, ділимо новий відрізок, який є підмножиною відрізка, знову на три рівні частини і виділимо ту, на якій немає точки (на цій "третини" не буде і точки, і точки, як це було встановлено вище). Далі новий відрізок знову ділимо на три рівні частини і вибираємо ту з них, де немає точкіа3 (як показано, точок ина ній також не буде), і так далі. В результаті наn- м кроці ми отримуємо відрізок довжини, на якому також немає точок ,,, .. Продовжуючи нескінченно цей процес, ми знаходимо точкуа. яка не включена в послідовність
Дійсно, а- загальна точка цих відрізків. Будучи точкою відрізка, вона повинна входити в зазначену послідовність, але це неможливо, тому що, яке б n ми не взяли, точка аn не може належати відповідному відрізку, а точка а буде йому належати, отже, а відмінна від всіх аn. що і доводить теорему.
Потужність множин, еквівалентних відрізку, назовемМОЩНОСТЬЮ континуум і позначимо буквойc.
Зазначимо деякі з таких множин.
Розглянемо відрізок. Записана нижче формула
,
встановлює взаємно однозначну відповідність між множиною і безліччю. Отже, має потужність континууму.
Крім того, безлічі:
мають ту ж потужність континууму c. так як відрізняються від безлічі кінцевим числом точок, що зберігає їх потужність.
Абсолютно несподіваний результат отримав Г. Кантор, припускаючи спочатку, що квадрат зі стороною, що дорівнює 1. містить "більше" точок, ніж відрізок. Вони виявилися еквівалентними.
"Я бачу це, але не вірю цьому", - повідомляв він у листі до Дедекіндом.
Дійсно, якщо квадрат розташувати в системі коордінатXOY. як зазначено нижче нарис. 7.9. то будь-якої його внутрішньої точкеW. має координати
можна поставити у відповідність точку інтервалу:
Різних точок W квадрата будуть відповідати різні точки інтервалу. Можна показати (використовуючи більш суворі міркування), що таке однозначне відповідність буде взаємно однозначним, тому безліч точок квадрата зі стороною, равной1. і відрізок мають однакову потужність. Більш того, не тільки квадрат, але, наприклад, куб або куля, містить "стільки ж" точок, скільки їх містить відрізок.
Порівняння безлічі натуральних чисел, що є рахунковим, і незліченної безлічі точок відрізка викликає питання: чи є безлічі проміжної потужності? Інакше кажучи, чи є безліч, в якому кількість елементів "більше", ніж натуральних чисел, і "менше", ніж точок на відрізку? Це є знаменітаяпроблемаКОНТІНУУМА. яка до сих пір хвилює багатьох математиків. На початку шістдесятих років
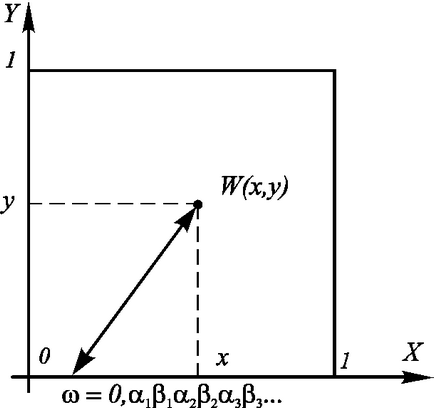
Мал. 7.9. Взаємно однозначна відповідність між точками всередині квадрата і точками інтервалу.
ХХ-го століття було встановлено, що існують як системи аксіом, в яких гіпотеза континууму істинна, так і аксіоматичні побудови, в яких вона помилкова.
В теорії множин доведені наступні твердження:
Для будь-якого безлічі A існує безліч більшої потужності (див. 2 і 3).
Безлічі найбільшій потужності не існує. (См.3).
Безліч всіх підмножин множини A має потужність більшу, ніж мощностьA.
Безліч всіх підмножин рахункового безлічі має потужність континууму.
Теорія множин сповнена проблем і парадоксів. які і в даний час викликають інтерес у дослідників. Один зних розглянуто вище. Тут наведемо классіческійпарадокс Б. Рассела.
Нехай M - множина всіх множин, а N - безліч всіх його підмножин. Тоді потужність множестваN всіх підмножин повинна бути більше потужності множестваM (за твердженням 3). Але по определеніюN - підмножина, звідси, N = M. Отримуємо непереборні протиріччя.