Урок і презентація на теми: "Натуральні логарифми. Підстава натурального логарифма. Логарифм натурального числа"
Що таке натуральний логарифм
Хлопці, на минулому уроці ми з вами дізналися нове, особливе число - е. Сьогодні ми продовжимо працювати з цим числом.
Ми з вами вивчили логарифми і знаємо, що в основі логарифма може стояти безліч чисел, які більше 0. Сьогодні ми також розглянемо логарифм, в основі якого стоїть число е. Такий логарифм прийнято називати натуральним логарифмом. У нього є власна запис: $ \ ln $ - натуральний логарифм. Такий запис еквівалентна запису: $ \ log_e = \ ln $.
Показові і логарифмічні функції є зворотними, тоді натуральний логарифм, є зворотною для функції: $ y = e ^ x $.
Зворотні функції є симетричними відносно прямої $ y = x $.
Давайте побудуємо графік натурального логарифма, відбивши експонентну функцію щодо прямої $ y = x $.
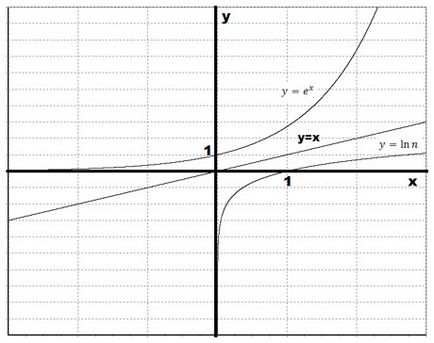
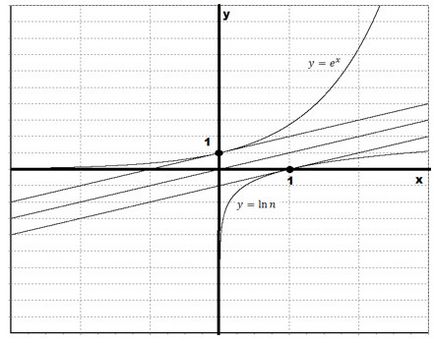
Варто зауважити кут нахилу дотичної до графіка функції $ y = e ^ x $ в точці (0; 1) дорівнює 45deg. Тоді кут нахилу дотичної до графіка натурального логарифма в точці (1; 0) також буде дорівнює 45deg. Обидві ці дотичні будуть паралельні прямій $ y = x $. Давайте схематично зобразимо дотичні:
Властивості функції $ y = \ ln $
1. $ D (f) = (0; + ∞) $.
2. Не є ні парною, ні непарною.
3. Зростає на всій області визначення.
4. Не обмежена зверху, не обмежена знизу.
5. Найбільшого значення немає, найменшого значення немає.
6. безперервного.
7. $ E (f) = (- ∞; + ∞) $.
8. опуклі вгору.
9. дифференцируемого всюди.
В курсі вищої математики доведено, що похідна оберненої функції є величина, зворотна похідною даної функції.
Заглиблюватися в доказ не має великого сенсу, давайте просто запишемо формулу: $ y '= (\ ln)' = \ frac $.
Приклад.
Обчислити значення похідної функції: $ y = \ ln (2x-7) $ в точці $ x = 4 $.
Рішення.
У загальному вигляді наша функція представляють функцію $ y = f (kx + m) $, похідні таких функцій ми вміємо обчислювати.
$ Y '= (\ ln)' = \ frac $.
Обчислимо значення похідної в необхідній точці: $ y '(4) = \ frac = 2 $.
Відповідь: 2.
Приклад.
Провести дотичну до графіка функції $ y = ln $ в точці $ x = е $.
Рішення.
Рівняння дотичної до графіка функції, в точці $ x = а $, ми добре пам'ятаємо.
$ Y = f (a) + f '(a) (x-a) $.
Послідовно обчислимо необхідні значення.
$ A = e $.
$ F (a) = f (e) = \ ln = 1 $.
$ F '(a) = \ frac = \ frac $.
$ Y = 1 + \ frac (x-e) = 1 + \ frac- \ frac = \ frac $.
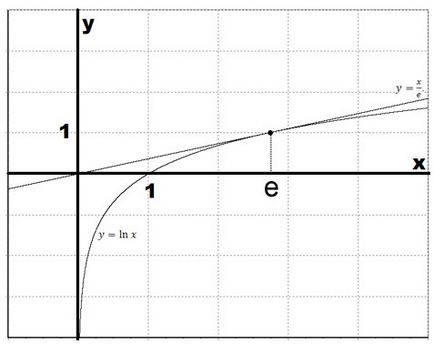
Рівняння дотичної в точці $ x = е $ являє собою функцію $ y = \ frac $.
Давайте побудуємо графік натурального логарифма і дотичній.
Приклад.
Дослідити функцію на монотонність і екстремуми: $ y = x ^ 6-6 * ln $.
Рішення.
Область визначення функції $ D (y) = (0; + ∞) $.
Знайдемо похідну заданої функції:
$ Y '= 6 * x ^ 5 \ frac $.
Похідна існує при всіх х з області визначення, тоді критичних точок немає. Знайдемо стаціонарні точки:
$ 6 * x ^ 5 \ frac = 0 $.
$ \ Frac = 0 $.
$ 6 * x ^ 6-6 = 0 $.
$ X ^ 6-1 = 0 $.
$ X ^ 6 = 1 $.
$ X = ± 1 $.
Точка $ х = -1 $ не належить області визначення. Тоді маємо одну стаціонарну точку $ х = 1 $. Знайдемо проміжки зростання та спадання:
Точка $ х = 1 $ - точка мінімуму, тоді $ y_min = 1-6 * \ ln = 1 $.
Відповідь: Функція убуває на відрізку (0; 1], функція зростає на промені $ [1; + ∞) $. $ Y_min = 1 $.
Хлопці, ми вміємо обчислювати похідні натурального логарифма і експоненційної функції. Але ми поки не знаємо, як обчислювати похідну будь-якого іншого логарифма і будь-який показовою функції.
Розглянемо показову функцію $ y = a ^ x $.
Згадаймо властивість: $ c ^> = b $.
Тоді: $ a = e ^ $.
$ A ^ x =)> ^ x = e ^ $.
Знайдемо похідну: $ (a ^ x) '= (e ^)' = \ ln * e ^ = \ ln * a ^ x $.
Похідна показовою функції дорівнює: $ (a ^ x) '= \ ln * a ^ x $.
Перейдемо до логарифмам, скористаємося формулою переходу до нового основи:
$ \ Log_a = \ frac> $.
Знайдемо похідну: $ (\ log_a) '= (\ frac>)' = \ frac * (\ ln) '= \ frac * \ frac = \ frac $.
Похідна логарифма за основою а числа х дорівнює:
$ (\ Log_a) '= \ frac $.
Завдання на натуральний логарифм для самостійного рішення
1. Обчислити значення похідної функції $ y = \ ln $ в точці $ x = 3 $.
2. Обчислити значення похідної функції $ y = \ log_4 $ в точці $ x = -2 $.
3. Знайти рівняння дотичної до графіка функції $ y = \ ln $ в точці $ x = 2е $. Схематично зобразити графік.
4. Дослідити функцію на монотонність і екстремуми: $ y = x ^ 8-4 * \ ln $.