При вирішенні наукових і інженерно-технічних завдань часто буває необхідно математично описати будь-яку динамічну систему. Найкраще це робити в вигляді диференціальних рівнянь (ДУ) або системи диференціальних рівнянь. Найбільш часто вони таке завдання виникає при вирішенні проблем, пов'язаних з моделюванням кінетики хімічних реакцій і різних явищ переносу (тепла, маси, імпульсу) - теплообміну, перемішування, сушіння, адсорбції, при описі руху макро- і мікрочастинок.
У ряді випадків диференціальне рівняння можна перетворити до вигляду, в якому старша похідна виражена в явному вигляді. Така форма запису називається рівнянням, дозволеним щодо старшої похідної (при цьому в правій частині рівняння старша похідна відсутня):
Рішенням звичайного диференціального рівняння називається така функція y (x), яка за будь-яких х задовольняє цьому рівнянню в певному кінцевому чи нескінченному інтервалі. Процес рішення диференціального рівняння називають інтегруванням диференціального рівняння.
Історично першим і найбільш простим способом чисельного розв'язання задачі Коші дляОДУ першого порядку є метод Ейлера. В його основі лежить апроксимація похідної ставленням кінцевих збільшень залежною (y) і незалежної (x) змінних між вузлами рівномірної сітки:
де yi + 1 це шукане значення функції в точці xi + 1.
Точність методу Ейлера можна підвищити, якщо скористатися для апроксимації інтеграла більш точною формулою інтегрування-формули трапецій.
Дана формула виявляється неявній щодо yi + 1 (це значення є і в лівій і в правій частині виразу), тобто є рівнянням щодо yi + 1. вирішувати яке можна, наприклад, чисельно, застосовуючи будь-якої ітераційний метод (в такому вигляді його можна розглядати як итерационную формула методу простої ітерації).
Склад курсової роботи: Курсова робота складається з трьох частин. У першій частині короткий опис методів. У другій частині постановка і рішення задачі. У третій частині - програмна реалізація на мові ЕОМ
Мета курсової роботи: вивчити два методи розв'язання диференціальних рівнянь-метод Ейлера-Коші і вдосконалений методЕйлера.
1. Теоретична частина
Звичайні диференціальні рівняння (ОДУ)
Диференціальні рівняння в приватних похідних.
Звичайними диференціальними рівняннями називаються такі рівняння, які містять одну або кілька похідних від шуканої функції. Їх можна записати вигляді
Найвищий порядок, що входить в рівняння (1) називається порядком диференціального рівняння.
Найпростішим (лінійним) ОДУ є рівняння (1) порядку дозволене відносно похідної
Рішенням диференціального рівняння (1) називається будь-яка функція, яка після її підстановки в рівняння звертає його в тотожність.
Основне завдання, пов'язана з лінійною ОДУ відомо як завдання Каші:
Знайти рішення рівняння (2) у вигляді функції задовольняє початковій умові (3)
Геометрично це означає, що потрібно знайти інтегральну криву, що проходить через точку) при виконання рівності (2).
Чисельний з точки зору завдання Каші означає: потрібно побудувати таблицю значень функції задовольняє рівняння (2) і початкова умова (3) на відрізку з деяким кроком. Зазвичай вважається, що то є початкова умова задано в лівому кінці відрізка.
Найпростішим з чисельних методів розв'язання диференціального рівняння є метод Ейлера. В його основі лежить ідея графічного побудови рішення диференціального рівняння, однак цей метод дає одночасно і спосіб знаходження шуканої функції в чисельній формі або таблиці.
Нехай дано рівняння (2) з початковою умовою тоесть поставлена задача Каші. Вирішимо спочатку таку задачу. Знайти найпростішим способом наближене значення рішення в певній точці де -досить малий крок. Рівняння (2) спільно з початковою умовою (3) задають напрямок дотичної шуканої інтегральної кривої в точці з координатами
Рівняння дотичної має вигляд
Рухаючись уздовж цієї дотичної, отримаємо наближене значення рішення в точці:
Маючи в своєму розпорядженні наближеним рішенням в точці можна повторити описану раніше процедуру: побудувати пряму проходить через цю точку з кутовим коефіцієнтом, і по ній знайти наближене значення рішення в точці
. Зауважимо, що ця пряма не є дотичною до реальної інтегральної кривої, оскільки точка нам не доступна, проте якщо досить мало то одержувані наближені будуть близькі до точних значень рішення.
Продовжуючи цю ідею, побудуємо систему рівно віддалених точок
Отримання таблиці значень шуканої функції
за методом Ейлера полягає в циклічному застосування формули
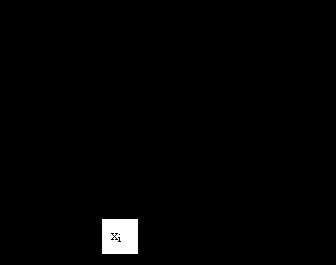
Малюнок 1. Графічна інтерпретація методу Ейлера
Методи чисельного інтегрування диференціальних рівнянь, в яких рішення виходять від одного вузла до іншого, називаються покроковими. Метод Ейлера найпростіший представник покрокових методів. Особливістю будь-якого покрокового методу є те, що починаючи з другого кроку початкове значення у формулі (5) саме є наближеним, тобто похибка на кожному наступному кроці систематично зростає. Найбільш використовуваним методом оцінки точності покрокових методів наближеного чисельного рішення ОДУ є спосіб подвійного проходження заданого відрізка з кроком і з кроком
1.1 Вдосконалений метод Ейлера
Основна ідея цього методу: що обчислюється за формулою (5) чергове значення буде точніше, якщо значення похідної, тобто кутовий коефіцієнт прямої замісної інтегральну криву на відрізку буде обчислюватися не по лівому краю (тобто в точці), а по центру відрізка. Але так як значення похідної між точками не вирахував, то перейдемо до здвоєним ділянкам центром, в яких є точка, при цьому рівняння прямої отримує вигляд:
А формула (5) отримує вид
Формула (7) застосована тільки для, отже, значення по ній отримати не можна, тому знаходять за методом Ейлера, при цьому для отримання більш точного результату надходять так: з початок по формулі (5) знаходять значення
У точці а потім знаходиться за формулою (7) з кроком
Після того як знайдено подальші обчислення при здійснюється за формулою (7)
1.2 Метод Ейлера-Коші
Геометрично це означає, що з початок визначається напрямок інтегральної кривої у вихідній точці і в допоміжній точці, а в якості остаточного напрямки береться середнє значення цих напрямків.
2. Постановка і рішення задачі
Вирішити диференціальне рівняння вдосконаленим методом Ейлера і методом Ейлера-Коші на прикладі рівняння н.у
2.1 Рішення завдання вдосконаленим методом Ейлера
Вирішити диференціальне рівняння вдосконаленим методом Ейлера на прикладі рівняння н.у з точністю
беремо крок. знаходимо:
Візьмемо як приклад рівняння н.у з точністю.
Результат роботи програми представлений на малюнку 2 а), б):
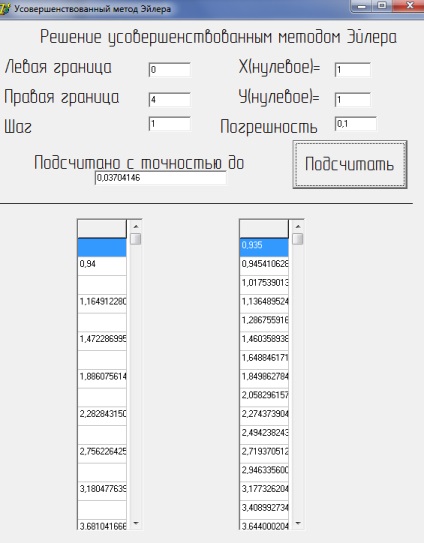
Малюнок 2 а) Реалізація на ЕОМ тестового прикладу вдосконаленого
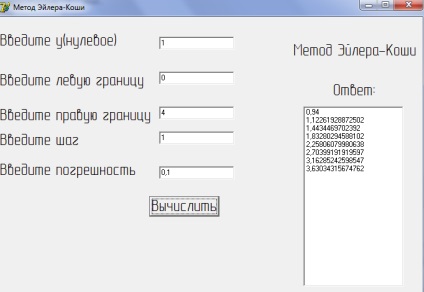
Малюнок 2 б) Реалізація на ЕОМ тестового прикладу методу Ейлера-Коші
Так, як заздалегідь відомо, рішення рівняння і воно збігається з отриманим в програмі результатом, то можна зробити висновок про те, що програма працює вірно.
Якщо введено а> b, то програма надійде в такий спосіб:
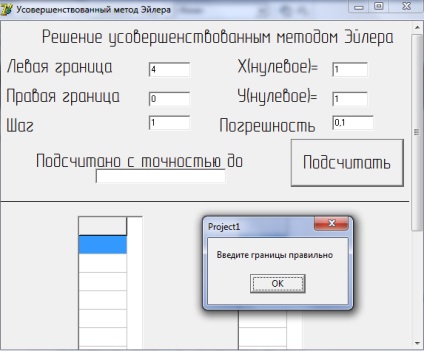
Малюнок 3 - Результат рішення рівняння вдосконаленим методом Ейлера при введенні а> b
Малюнок 4 - Результат рішення рівняння методом Ейлера-Коші при введенні а> b
Якщо похибка введена неправильно, то програма надійде в такий спосіб:
Малюнок 5 - Результат рішення рівняння вдосконаленим методом Ейлера при неправильно введеної похибки
Малюнок 6 - Результат рішення рівняння методом Ейлера-Коші при неправильно введеної похибки
3.4. Рішення завдання за допомогою ЕОМ
Візьмемо як приклад рівняння н.у з точністю.
При вирішенні заданого рівняння на мові програмування Borland Delphi, ми отримуємо наступні результати (малюнок 3):
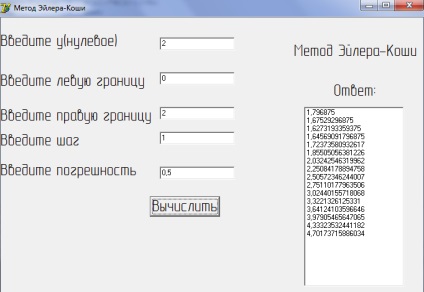
Малюнок 7Реалізація на ЕВМметода Ейлера-Коші
Візьмемо як приклад рівняння н.у з точністю.
При вирішенні заданого рівняння на мові програмування Borland Delphi, ми отримуємо наступні результати (малюнок 4):
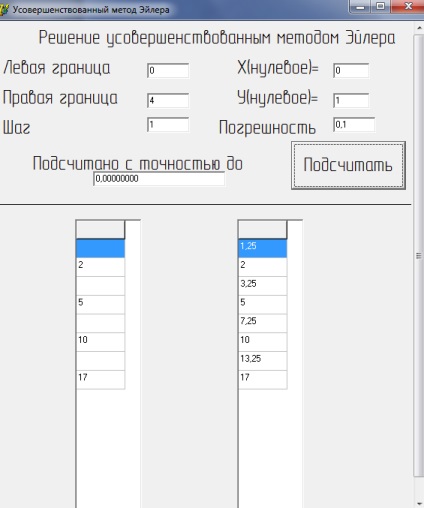
Малюнок 8Реалізація на ЕОМ усовершенствованногометода Ейлера
У таблицях 1 і 2 представлений результат роботи програм при завданні різних вихідних даних.
Таблиця 1 - Результати роботи програми для вдосконаленого методу Ейлера
висновок
Таким чином, очевидно, що при обчисленні диференціального рівняння методами Ейлера-Коші і Удосконалений метод Ейлера рішення не дає нам точного значення, а тільки наближене.
Чим менше задається інтервал обчислення і крок операцій, тим точніше результат, одержуваний машиною. Для більшої точності необхідно більше число ітерацій, що зумовлює зростання витрат часу обчислення інтеграла на комп'ютері обернено пропорційно точності обчислення.
Використання для обчислення одночасно двох методів дозволило дослідити залежність точності обчислень при застосуванні обох методів. На чому можна зробити певний висновок що, вдосконалений метод Ейлера легший для машини і результат (який дуже близький до точного) отримуємо швидше методу Ейлера-Коші. Але метод Ейлера-Коші є більш точним.
Програми написані на мові Borland Delphi для вирішення диференціальних рівнянь. Отримані в результаті роботи програм рішення збігаються з відповідями в прикладі
Список використаної літератури
Самарський А. А. Гулін А. В. Чисельні методи: Учеб. посібник для вузів. - М. Наука. Гл. ред. фіз-мат. лит. 1989. - 432 с.
Схожі роботи:
Ітераціональние методирешенія нелінійних рівнянь
). Класифікація методоврешенія і чисельних методів інтегрування діфференціальнихуравненій. Поняття задачі Коші і кроку інтегрування. Метод послідовних наближень (метод Піккара). МетодЕйлера.
Ейлер. Ейлер продовжував розробку теорії діфференціальнихуравненій. розпочату в роботах Лейбніца і Бернуллі. Теорія діфференціальнихуравненій. О. Коші створив. Морзе створив вдосконалений телеграф, в. методу "проб і помилок" як засіб вирішення.
Методи комп'ютерних обчислень і їх додаток до фізичних завдань
Приклад - діфференціальноеуравненіе з початковими умовами. Загальна решеніедіфференціальногоуравненія є. 1 ... m - число рівнянь. k - номер попередньої обчисленої точки. УсовершенствованнийметодЕйлера -Коші з уточненням. Даний метод базується на.
Шпаргалка >> Інформатика, програмування
підвищення надійності виконання програм, надає вдосконалені 32-розрядні компоненти і, в той. Розглянемо деякі чисельні методирешенія такого рівняння. 1.4. Метод простих ітерацій. Нехай задано рівняння f (x) = 0, де f (x) -.