Цей метод не має обмежень по виду правих частин системи (1) або (4), крім умов існування і єдиності рішення. Він може бути застосований для дослідження стійкості рухів будь-яких систем диференційних рівнянь, але, на жаль, аж до теперішнього часу не розроблено загальний метод побудови функцій Ляпунова, необхідних для вирішення питань стійкості руху нелінійних систем.
При дослідженні стійкості рухів нелінійних систем типу (1) цим методом також розглядається система диференціальних рівнянь у відхиленнях (4). Завдання полягає у визначенні умов на вектор-функцію. при яких положення рівноваги цієї системи асимптотично стійко. Як зазначалося вище, положення рівноваги системи (4) стійко асимптотично, якщо її вектор стану задовольняє умовам (11).
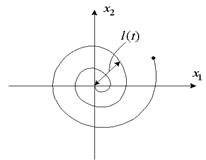
Якщо положення рівноваги системи стійко асимптотично, то відстань зображає точки від початку координат з плином часу зменшується, можливо, немонотонно, як для прикладу показано на рис. 4. Якщо ж особлива точка системи не є асимптотично стійкою, то ця відстань не зменшується при.
Ідея другого методу Ляпунова полягає в побудові деякої функції. залежної від вектора стану досліджуваної системи, позитивної і монотонно спадної зі зменшенням. Якщо ця функція при буде прагнути до нуля, подібно віддалі зображає точки від положення рівноваги, то, очевидно, відповідне положення рівноваги буде асимптотично стійким.
Іншими словами, стійкість або нестійкість невозмущенного руху системи можна встановити, дослідивши характер зміни функції з плином часу.
Такі функції отримали назву функцій Ляпунова. Функції Ляпунова зазвичай завжди більше нуля і мають негативну похідну за часом (в разі стійкості положення рівноваги), визначену на траєкторіях досліджуваної системи.
У зв'язку з цим розглянемо поняття знакоопределенних функцій, т. Е. Позитивно (негативно) певних і знакопостоянного позитивно (негативно) полуопределенних функцій, а також поняття похідної за часом уздовж траєкторій динамічної системи.
Розглянемо функцію. Нехай ця функція диференційована, тобто її приватні похідні існують при всіх.
Визначення. Функція називається позитивно-певної, якщо при будь-якому
Позитивно-певна функція позначається. Позитивно-визначеними функціями при є, наприклад, функції
Визначення. Функція називається позитивно полуопределённой, якщо
Позитивно полуопределенная функція позначається. Позитивно полуопределенной функцією при є, наприклад, функція
Негативно-певна функція визначається так:
Негативно-певна функція позначається. а негативно полуопределенная.
Визначення. Функція називається нескінченно великою, якщо для будь-якого числа знайдеться таке, що поза сферою має місце нерівність.
Квадратичні форми. Часто в якості знакоопределенних функцій використовуються квадратичні форми, т. Е. Функції виду
Матриці Р квадратичних форм зазвичай є симетричними матрицями, т. Е. Такими, у яких
Умови позитивної визначеності квадратичної форми із симетричною матрицею полягають у наступному.
Критерій Сильвестра. Для позитивної визначеності квадратичної форми (13), (14) необхідно і достатньо, щоб всі діагональні мінори матриці Р були строго більше нуля.
Матриці Р, що задовольняють критерію Сильвестра, називають позитивно-визначеними і також позначають.
Нехай матриця Р симетрична, т. Е.
Для оцінки знакоопределенності цієї матриці знайдемо такі визначники:
Тоді відповідно до критерію Сильвестра матриця. якщо
Визначення похідної за часом уздовж траєкторії системи. Ця похідна грає велику роль при дослідженні стійкості рухів динамічних систем методом функцій Ляпунова. Розглянемо деяку функцію. певну на змінних станах системи (4). Знайдемо її похідну за часом уздовж траєкторій цієї системи. За загальним правилом диференціювання складної функції знаходимо
Однак в силу рівняння (4). Тому похідна за часом від функції V (x) уздовж траєкторії системи (4) визначається виразом
Приклад 2. Нехай. а рівняння системи мають вигляд. Знайти похідну за часом функції вздовж траєкторій заданої системи.
Рішення. За формулами (16), (17) знаходимо
або з урахуванням заданих рівнянь для і:
Як видно, похідна є негативно-визначеною. Це вказує на те, що функція монотонно загасає, зменшуючись за величиною при. Так як може зменшуватися лише при зменшенні. то норма вирішення даної системи, очевидно, прагне до нуля при. Причому це має місце при будь-яких початкових умовах. Отже, положення рівноваги даної системи є асимптотично стійким в цілому.
Зауважимо, що цей висновок зроблений без рішення диференціальних рівнянь заданої нелінійної системи, і будь-яких інших математичних операцій над ними.
Основу другого методу Ляпунова для дослідження рухів динамічних систем складають наступні теореми [2, 20].
Теорема 4 (асимптотичну стійкість). якщо при
всіх існує позитивно-визначена функція така, що її похідна по часу вздовж траєкторій системи (4) є негативно-певною функцією, то становище рівноваги цієї системи асимптотично стійко в цілому.
Теорема 5 (про нестійкість). Якщо при всіх. існує позитивно-визначена функція така, що її похідна по часу вздовж траєкторій системи (2) також є позитивно-певної функцією, то становище рівноваги такої системи нестійка.
Теорема 6 (Барбашина-Красовського). Якщо при всіх існує нескінченно велика позитивно-визначена функція така, що її похідна по часу вздовж траєкторій системи (4) є негативно полуопределенной функцією, але звертається в нуль на безлічі, що не містить цілих траєкторій, (крім положення рівноваги) системи (4), то положення рівноваги системи (4) асимптотично стійко в цілому.
Позитивно-певна функція. задовольняє будь-якої теоремі про стійкість або нестійкість по відношенню до деякої системи, називається функцією Ляпунова даної системи. Відзначимо також, що якщо функція Ляпунова задовольняє умовам деякої теореми про стійкість не в усьому просторі, а лише в деякій області, що включає положення рівноваги, то ця область є областю тяжіння відповідного положення рівноваги.
Наведемо приклади дослідження стійкості рухів нелінійних систем методом функцій Ляпунова.