Тобто рішення Х * також є оптимальним.
Теорема 1 вказує принцип вирішення завдань ЛЗ: замість дослідження нескінченної кількості допустимих рішень необхідно досліджувати кінцеве число кутових точок.
1.3. Графічний метод розв'язання задачі ЛП з двома змінними
Дана задача ЛП з двома змінними
Графічний метод рішення заснований на можливості графічного зображення ОДР завдання і знаходження в ній оптимального рішення.
1. Будують ОДР завдання як перетин областей рішень кожного з заданих обмежень. ОДР може бути опуклий багатокутник; опукла багатокутна необмежена область; порожня область; промінь; відрізок; єдина точка. Якщо ОДР є порожнім безліччю, завдання не має рішення виду несумісності системи обмежень.
2. Якщо ОДР непусто, визначають напрям зростання цільової функції Z (X).
При довільному фіксованому значенні рівняння визначає на площині пряму, яка є лінією рівня цільової функції - прямий, на якій цільова функція завдання приймає постійне значення. Загальний вигляд рівняння лінії рівня: с1x1 + с2x2 = l, l = const. Всі лінії рівня паралельні між собою. Їх нормаль. Напрямок є напрямком возрастаніяZ (X).
Таким чином, на 2-му етапі будують нормаль ліній рівня та одну з ліній рівня (що має загальні точки з ОДР).
3. Лінію рівня переміщають паралельно в напрямку нормалі в завданні на максимум, в протилежному напрямку в завданні на мінімум. У якийсь момент вона займе граничне положення: 1) буде мати хоча б одну спільну точку з ОДР, 2) ОДР буде знаходитися в одній півплощині по відношенню до лінії рівня. Така лінія рівня називається опорною прямий. ОДР будь-якого завдання ЛП має не більше двох опорних прямих, на одній з яких може перебувати оптимальне рішення.
4. Якщо при переміщенні лінії рівня по ОДР у відповідному напрямку лінія рівня йде в нескінченність, то задача не має оптимального рішення з огляду на необмеженість цільової функції. Пишуть Z (X) →.
5. Якщо завдання має оптимальне рішення, для його знаходження необхідно вирішити спільно рівняння прямих, що обмежують ОДР і мають спільні точки з опорної прямої.
6. Обчислюють значення цільової функції на оптимальному рішенні.
Залежно від виду ОДР і цільової функції Z (X) завдання ЛП може мати єдине рішення, безліч рішень, не мати оптимального рішення (див. Рис. 1, 2, 3).
На рис.1 лінія рівня двічі стає опорною по відношенню до багатокутника рішень. Мінімальне значення Z (X) досягається в т. А, максимальне - в т. С.
На рис.2 опорна пряма збігається з однією з сторін багатокутника рішень. Оптимальним рішенням є будь-яка опукла лінійна комбінація точок відрізка АЕ.
На рис.3 ОДР не обмежена в бік збільшення значень Z (X).
Приклад 1. Вирішимо графічно задачу ЛП:
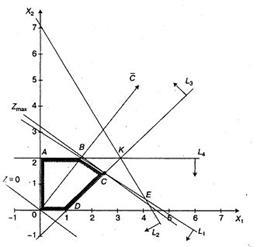
Побудуємо багатокутник рішень (рис.4). Для цього в системі координат X10X2 на площині зобразимо граничні прямі:
3х1 + 2х2 = 13 (L2);
Взявши будь-яку точку, наприклад, початок координат, встановимо, яку полуплоскость визначає відповідне нерівність. Напівплощини, що визначаються нерівностями, на рис.4 показані стрілками. Областю рішень є багатокутник OABCD.
Будуємо лінію рівня Z = 3х1 + 4х2 = 0 і вектор-градієнт. Пряму Z = 0 перемещаем паралельно самій собі в напрямку вектора. З рис.4 випливає, що по відношенню до багатокутника рішень опорної ця пряма стає в точці C. де функція приймає максимальне значення.
Точка С лежить на перетині прямих L1 і L3. Для визначення її координат вирішимо систему рівнянь:
Оптимальний план задачі х1 = 2,4; х2 = 1,4. Підставляючи значення х1 і х2 в лінійну функцію, отримаємо:
.
1.4. Рішення задач лінійного програмування симплекс-методом
Приведення завдань ЛП до канонічної формі
Якщо математична модель задачі ЛП має вигляд:
то кажуть, що завдання представлена в канонічній формі на мінімум (максимум).
Більш компактна запис:
(1) і (2) - координатні записи канонічної задачі ЛП.
Векторна запис канонічної задачі:
Матрична запис канонічної задачі:
Будь-яке завдання ЛП можна звести до канонічної за такими правилами.
1. Перехід від завдання на max до задачі на min (і назад) здійснюється зміною знака цільової функції
Вихідна і отримана завдання мають один і той же оптимальне рішення Х *, а значення цільових функцій на цьому рішенні відрізняються лише знаком.
2. Якщо серед обмежень є нерівності, то шляхом введення додаткових невід'ємних змінних вони перетворюються в рівності
У цільову функцію додаткові змінні вводяться з нульовими коефіцієнтами, в цьому випадку вони не впливають на значення Z (X)
3. Якщо деяка змінна xk не має обмежень по знаку, то вона замінюється (в цільової функції і у всіх обмеженнях) різницею між двома новими невід'ємними змінними:, де.
Приклад 1. Наведемо до канонічної формі (на мінімум) задачу ЛП:
1. Перейдемо до задачі на мінімум
2. Введемо в кожне обмеження системи обмежень вирівнюють змінні x 4, x 5, x 6. Система запишеться у вигляді рівності.
.
3. У канонічній формі записи завдань ЛП всі змінні, що входять в систему обмежень, повинні бути негативними. Припустимо, що, де.
Підставляючи цей вираз в систему обмежень і цільову функцію і записуючи змінні в порядку зростання індексу, отримаємо задачу ЛП, представлену в канонічній формі:
Принцип роботи симплекс-методу
Рішення задач ЛП на основі симплекс-методу полягає в цілеспрямованому переборі кутових точок ОДР в напрямку поліпшення значення цільової функції.
Спочатку знаходиться будь-яке допустиме рішення, відповідне однією з кутових точок ОДР. Перевіряються суміжні з нею кутові точки, тобто розташовані на тій же кордоні ОДР, що і поточна кутова точка (для двомірної ОДР - на тій же стороні багатокутника, для тривимірної - на тому ж ребрі багатогранника і т. Д.).
Можна довести, що перехід з однієї кутової точки ОДР в іншу (суміжну) відповідає заміні однієї змінної в базисі. Така заміна означає, що одна з небазисних змінних (мала нульове значення) включається в базис, т. Е. Збільшується, а одна з базисних змінних зменшується до нуля, т. Е. Виключається з базису. Вибір таких змінних виконується за певними правилами, що забезпечує максимально швидке поліпшення цільової функції.
Якщо в жодній із суміжних кутових точок значення цільової функції не поліпшується, то рішення задачі завершується; поточна кутова точка ОДР відповідає оптимальному вирішенню завдання. Якщо є суміжні кутові точки ОДР, для яких значення цільової функції поліпшується, то у разі переходу до ту з них, для якої досягається найбільш швидке поліпшення значення цільової функції. Для нової кутовий точки ОДР процес повторюється. Перебір кутових точок відбувається до тих пір, поки не буде знайдено оптимальне рішення, т. Е. Поки не буде досягнута кутова точка ОДР, для якої ні в одній з суміжних точок значення цільової функції не поліпшується.
Метод називається симплексним, т. К. Області допустимих рішень задач, які розглядалися на початковому етапі розвитку методу, мали найпростіший (simple) вид (рис.1):
1.Задача приводиться до канонічної формі.
2.Строітся вихідна симплекс-таблиця і визначається початкова дозволене рішення (початкова кутова точка).
3.Виполняются перетворення симплекс-таблиць, відповідні перебору кутових точок ОДР, до отримання оптимального рішення.
Розглянемо реалізацію даного алгоритму при вирішенні задачі лінійного програмування:
1. Перепишемо задачу в канонічному вигляді, додавши додаткові невідомі:
2. Запишемо першу симплекс-таблицю:
Якщо в останньому рядку (серед чисел -c1, .... -c2) немає негативних коефіцієнтів, то базисне рішення (коли вільні невідомі х1 = ... = хn = 0) буде оптимальним. Дійсно, якщо збільшити від 0 хоча б одне з вільних невідомих, то функція буде спадати.
Нехай, наприклад, -c1 <0, тогда, увеличивая число х1 будем получать большие значения функции. Если число a11>0, то при рівності 0 всіх інших вільних невідомих х1 можна збільшувати не більше ніж до числа b1 / a11. Якщо a11 0, то нерівність не накладає обмежень на зростання числа х1 (тоді х1 можна збільшувати скільки завгодно). Тому, якщо все коефіцієнти a11, ..., ak1 непозитивні, то х1 може рости необмежено і, при цьому, функція буде наростати також необмежено. В цьому випадку оптимального рішення немає.
3. Обмежимося випадками, коли в першому стовпці серед чисел a11, ..., ak1 є позитивні коефіцієнти:, тоді число х1 можна збільшувати до величини x0 = min. Нехай min досягається в рядку і нехай i1 = 1. Перейдемо до базису, переводячи х1 в базис замість хn + 1. Отримаємо нову симплекс-таблицю, для якої значення функції зросте на число з1 х0> 0.
Для нової симплекс-таблиці, якщо в останньому рядку немає негативних коефіцієнтів, відповідне базисне рішення буде оптимальним (функція має вигляд, де числа, ..., 0 і тому збільшувати числа х1, ..., хn + 1 невигідно). Якщо в останньому рядку буде негативний коефіцієнт, то виконуємо попередню процедуру (по переходу до нової симплекс таблиці) ще раз. За кінцеве число кроків ми отримаємо оптимальне базисне рішення або доведемо, що оптимального рішення немає.
Приклад 2. Для виконання робіт з виготовлення виробів 1-го і 2-го типу є 10 одиниць 1-го сировини і 8 одиниць 2-го сировини. На кожен виріб 1-го типу витрачається по 2 одиниці кожного сировини, а для кожного виробу 2-го типу витрачається 4 і 1 одиниці сировини кожного типу. Спланувати виробництво так, щоб сумарна кількість виробів було найбільшим.
Нехай виробів 1-го і 2-го типу виробляється x1 і x2 одиниць, тоді сировини 1-го типу буде витрачено, а сировини 2-го типу. Потрібно знайти максимум функції при невід'ємних цілих значеннях аргументу.
Введемо допоміжні невідомі x3 і x4 (залишки сировини 1-го і 2-го типу) і отримаємо канонічну задачу:
Складемо вихідну симплекс-таблицю: