У загальному випадку може бути задано безліч початкових і безліч кінцевих станів системи
Необхідно знайти управління. переводить систему з області в область за хв. час.
В даному випадку для оптимізації процесу необхідно, щоб існувала безперервна векторна функція, яка задовольнить не тільки умовою максимуму, але іумов трансверсальності в обох кінцях траєкторії (t).
Умови трансверсальності полягають у тому, щоб вектор був ортогонален площинами, дотичними до областям і відповідно на початку і в кінці траєкторії. Будемо вважати, що функції ограніченійінепреривни і безперервно діфференцируєми поx. Припустимо також, що області і обмежені, замкнуті і опуклі.
Розглянемо, яким умовам повинна задовольняти функція (t), якщо початкова точка належить області початкових станів а кінцева точка є початком координат.
Оскільки - замкнутий безліч, точка є граничною точкою цієї множини: якби вона такою не була, то треба було б час на те, щоб вийти за кордон безлічі, а це було б не оптимально.
Нехай - початкова точка оптимального процесу. Час руху з цієї точки в кінцеву. Побудуємо область досяжних станів, відповідних часу t.
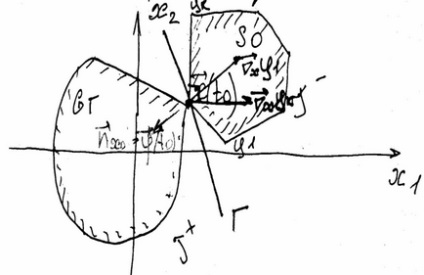
Т.ч. виходить, що початкова точка є граничною точкою двох множин: множини вихідних і безлічі досяжних за времяT станів.
По теоремі Хана-Банаха, два опуклих і непересічних безлічі можуть бути розділені однієї гиперплоскостью. Якщо ці області мають одну спільну точку, то дана гіперплоскость є опорною до областям в цій точці.
Проведемо гіперплоскость Г. Якщо гіперплоскость Г розглядати як опорну до області досяжних станів, то нормаллю до цієї гіперплощини буде вектор.
Знайдемо зв'язок між і нормалями до обмежень: Нормалі будуть спрямовані внутрьS0. тому
Для тих обмежень, які неефективні по теоремі Куна-Таккера,. тоді отримуємо
Якщо рух починається з точки і закінчується в області, то умова буде ось таким:
Сукупність цих двох умов називається умовами трансверсальності.
Зауваження: якщо кінцева область є точкою, товибірается довільно. Якщо область мети - все фазовий простір, то = 0, так як все коеффіціентибудут нульовими (а всі обмеження, відповідно, неефективними).
8.Прінціп максимуму для задач управління стаціонарними системами з інтегральним критерієм якості.
Завдання управління з інтегральним критерієм якості:
ФункціяLнепреривна по своїх аргументів і має безперервні приватні похідні .. Якщо функціяL = 1, то завдання оптимального швидкодії.
Умова принципу максимуму для стаціонарних систем:
Завдання управління з інтегральним критерієм якості, коли функціонал, область мети і рівняння стани не залежать явно від часу.
Нехай стан динамічної системи описується нелінійним диф. рівнянням виду:.
Задані обл. початкового стану S0 і конечногоSf. Потрібно визначити умови, кіт. удовл. Оптимальне керування з області допустимих і траєкторію, що відповідає оптимальному управлінню, що задовольняє граничним умовам.
.
Вважаємо, що кінцевий момент часу tне заданий.
Припустимо, що Lне залежить явно від часу і позитивна.
Переходимо від деякого реального часу tк деякого фіктивному времені .. З урахуванням цього вихідна система діф.ур. набуде вигляду :. (). Тоді функціонал относітельнопрінімает вид: (*) - звели до задачі оптимальної швидкодії.
Перенесемо отримані умови для задач оптимального швидкодії на більш широкий клас задач. Нехай () оптимальний процес в смислеminформули (*), тоді він задовольняє принципу максимуму для задачі оптимальної швидкодії.
Існує функція, відносять. Кіт. вип. умови: ;; де
Виконується умова максимуму:
Уздовж оптимальної траєкторії функція Гамільтона має наступний вигляд:
Виконується умова трансверсальності.
Введемо в розгляд функцію структури, підставимо вир-е для ф-ії Гамільтона (1)
(2) Ця функція зв. Гамильтонианом системи з інтегральним критерієм якості. Гамільтоніан = 0 тільки уздовж оптимальної траєкторії. У загальному випадку, коли немає залежності від часу: (3).
Введення гамильтониана дозволяє узагальнити умова максимуму, тобто можна сказати, що якщо () -опт. процес, то повинні виконуватися наступні умови:
Повинна існувати функція, для кіт. справедливі слід. співвідносячи-ия: а); б)
Виконується умова максимуму:
Гамільтоніан уздовж оптимальної траєкторії = 0.
Виконується умова трансверсальності.
Перейдемо від умовного часу к реальному часу t:
,- умова 1а виконується.
Перевіримо (1б):, переходимо откt:, - умова 1б виконується.
Перевіряємо ум. 2:, отже ,,
Ум. 3: Гамільтоніан уздовж опт. траєкторії = 0, це випливає з його виведення і грунтується на усл.2
Ум. 4: Оскільки в умова трансверсальності ні ф-ція Гамільтона ні Гамільтоніан не входять, то вони повністю сохр. свій вигляд:
Замечаніе1: Ми отримали умова maxв припущенні, що, але вони виконуються і в загальному випадку.
Замечаніе2: ConstP0 зазвичай вважають = -1. P0 = -1