Гіперболою називається геометричне місце точок площини, для кожної з яких абсолютне значення різниці відстаней до двох даних точок площини і. званих фокусами, є величина постійна, рівна 2a.
Відстань між фокусами - 2c.
Якщо осі декартової прямокутної системи координат вибрані так, що фокуси даної гіперболи розташовуються на осі абсцис симетрично відносно початку координат (рис. 2.13.1), то канонічне рівняння гіперболи має вигляд
Де. Рівняння виду (2.13.1) називається канонічним рівнянням гіперболи. При зазначеному виборі системи координат осі координат є осями симетрії гіперболи. а початок координат - її центром симетрії. Ось Ox називається дійсною віссю. а Oy - уявною віссю гіперболи. Точки перетину гіперболи з віссю називаються вершинами гіперболи.
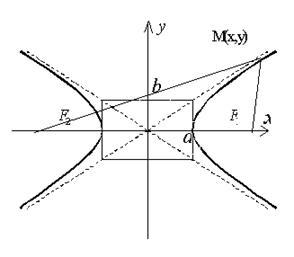
Прямокутник зі сторонами 2a і 2b. розташований симетрично щодо осей гіперболи і що стосується її в вершинах, називається основним прямокутником гіперболи. Діагоналі основного прямокутника (необмежено продовжені) є асимптотами гіперболи і визначаються рівняннями
Ексцентриситетом гіперболи (як і еліпса) називається число. де a - відстань від центру гіперболи до її вершини. Очевидно, що для будь-якої гіперболи e> 1.
Якщо M (x; y) - довільна точка гіперболи, то відрізки і називаються фокальними радіусами точки М. Фокальні радіуси правійгілки гіперболи можуть бути обчислені за формулами і. Фокальні радіуси лівої галузі гіперболи - за формулами і.
Якщо гіпербола задана рівнянням (2.13.1), то прямі, що визначаються рівняннями. називаються її директрисами.
Скласти рівняння гіперболи, фокуси якої лежать на осі абсцис, симетрично відносно початку координат, якщо точка лежить на гіперболі і відомі рівняння асимптот.
З рівнянь для асимптот знаходимо. або. Оскільки точка належить гіперболі, її координати задовольняють рівняння (2.13.1):. де або. Звідси знаходимо. тоді. отже, рівняння гіперболи має вигляд.
Дана гіпербола. Знайти її піввісь a і b. фокуси, ексцентриситет, рівняння асимптот.
Розділимо обидві частини цього рівняння на 144. Отримаємо. Значить a = 3, b = 4, отже осі гіперболи відповідно рівні 2a = 6 і 2b = 8. Так як . то фокуси гіперболи знаходяться в точках і. Ексцентриситет гіперболи обчислюється за формулою. Відповідно до (2.13.2), рівняння асимптот мають вигляд:.
Парабола, її директриса
Параболою називається геометричне місце точок площини, для кожної з яких відстань до деякої фіксованої точки площини F. званої фокусом. дорівнює відстані до деякої фіксованої прямої, званої директоркою.
Нехай дана деяка парабола. Введемо декартову прямокутну систему координат так, щоб вісь абсцис проходила через фокус даної параболи перпендикулярно директрисі і була спрямована від директриси до фокусу. Початок координат розташуємо посередині між фокусом і директоркою (рис. 2.14.1). У цій системі координат дана парабола буде визначатися рівнянням:
де p - відстань від фокуса до директриси (параметр параболи). Рівняння (2.14.1) є канонічне рівняння параболи.
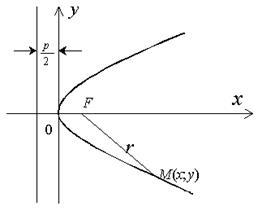
Директриса даної параболи визначається рівнянням. Фокальний радіус довільної точки M (x; y) параболи може бути обчислений за формулою
Парабола має одну вісь симетрії, яка називається віссю параболи, з якої вона перетинається в єдиній точці. Точка, в якій парабола перетинається з віссю симетрії, називається вершиною параболи. При зазначеному вище виборі системи координат вісь параболи поєднана з віссю абсцис, вершина знаходиться на початку координат, а вся парабола лежить в правій півплощині.
Якщо вершину параболи (2.14.1) перенести в точку. то її канонічне рівняння набуде вигляду.
Знайти фокус F і рівняння директриси параболи.
Параметр даної параболи p = 12. Оскільки відстань від фокуса до директриси одно. то фокус має координати F (6; 0). а рівняння директриси. тобто x + 6 = 0.
Скласти рівняння параболи з вершиною в початку координат і фокусом в точці F (0; 8).
Оскільки фокус параболи лежить на осі ординат, а її вершина - на початку координат, то рівняння параболи можна записати у вигляді. Так як ордината фокуса негативна, то рівняння параболи слід шукати у вигляді.
Фокусна відстань . звідки 2p = 32. Отже, рівняння параболи має вигляд.