Генценовскіе обчислення натурального виведення

§1. Обчислення nj.

Визначення 2.1.NJ - висновок складається з формул, розташованих у вигляді дерева.

Визначення 2.2.Допущенія - це вихідні формули виведення, кожному у тому числі в виведенні поставлена ​​у відповідність до точності одна Н-фігура укладення (при цьому дана вихідна формула варто «вище» нижньої формули цієї Н-фігури ув'язнення.)

Всі формули, які стоять нижче даного допущення і одночасно вище нижньої формули тієї Н-фігури укладення, якій співставлено дане припущення, а також саме дане припущення називаються залежними від даного допущення. Таким чином, висновок робить отримане в його результаті висловлювання незалежним від сопоставленного йому допущення.

У відповідності зі сказаним, кінцева формула виведення не залежить ні від яких припущень.

Схеми фігур укладення

Введення кон'юнкції: Видалення кон'юнкції:

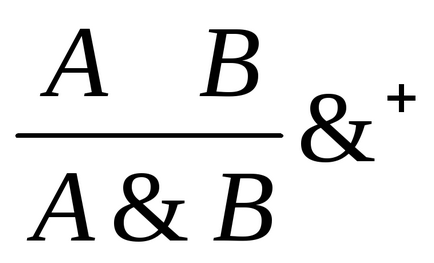
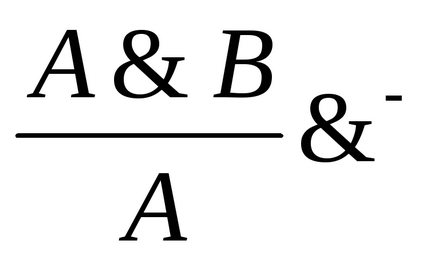
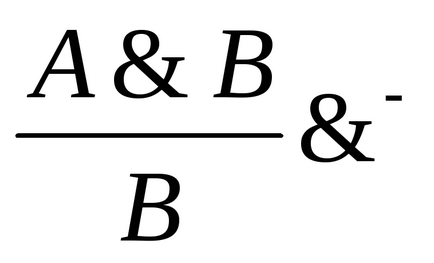
Введення диз'юнкції: Видалення диз'юнкції:

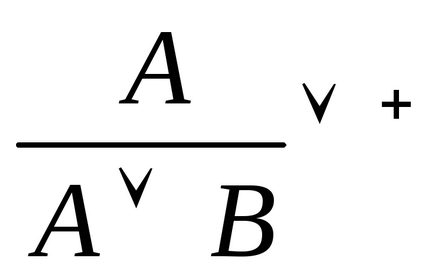
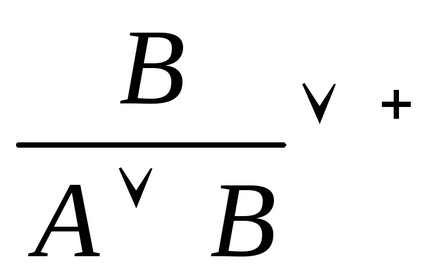
Введення імплікації: Видалення імплікації:

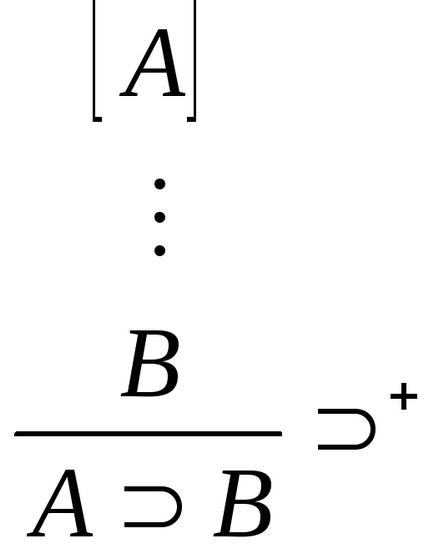
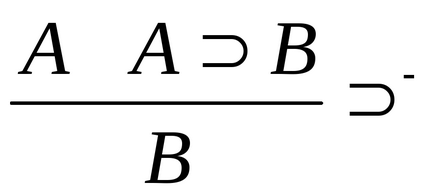
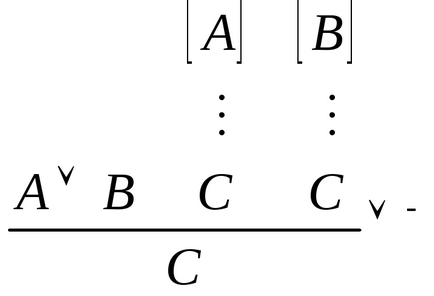
Введення заперечення: Видалення заперечення:

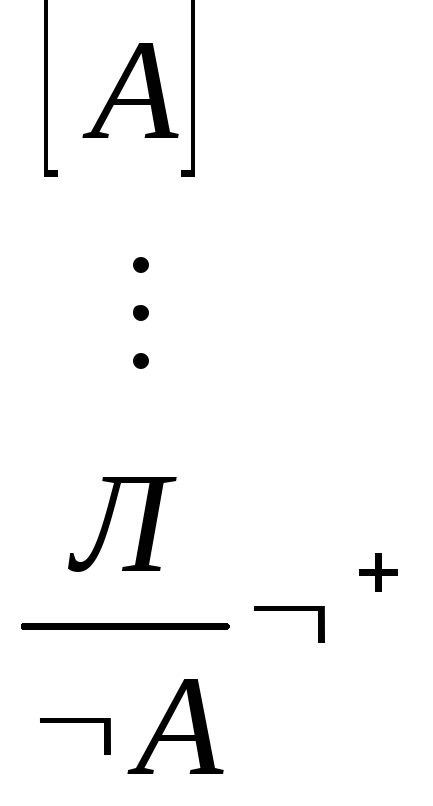
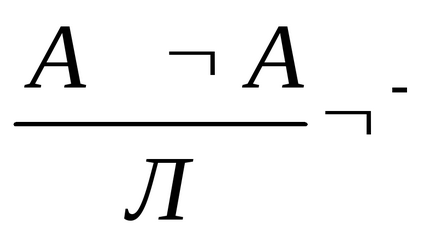
Введення довільного висловлювання:

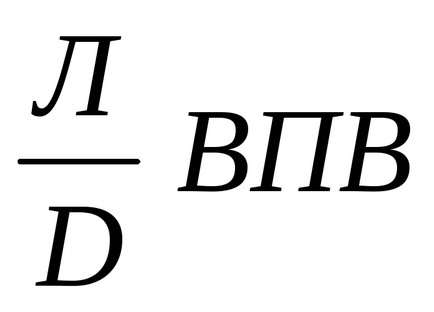
Введення квантора загальності: Видалення квантора загальності:

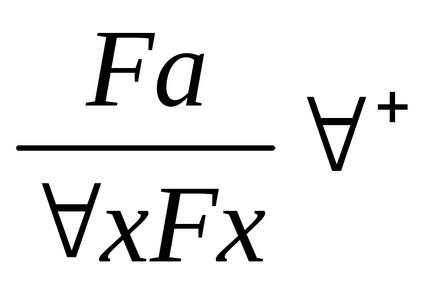
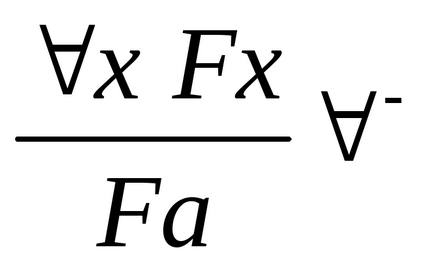
Введення квантора існування: Видалення квантора існування:

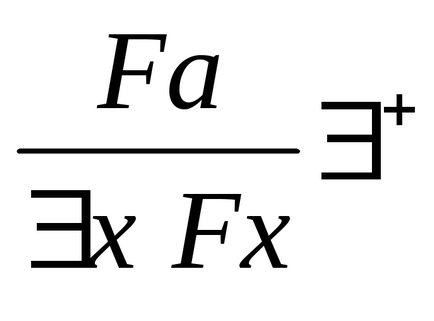
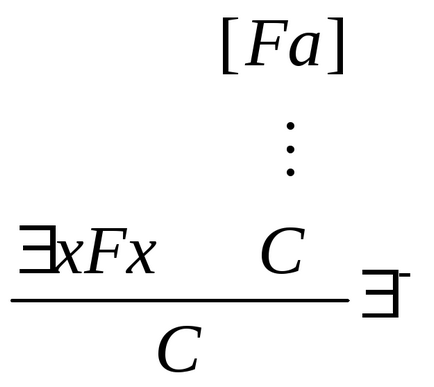
Власної змінної деякої фігури укладення

(відповідно) Ми називаємо вільну предметну змінну, позначену у відповідній схемі посредствома; передбачається, що вона існує, тобто пов'язана предметна змінна, позначена посредствомx. входить в формулу позначену посредствомFx.

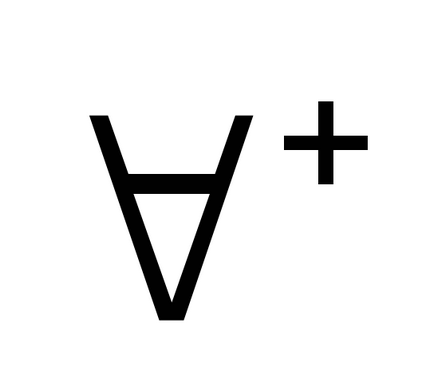
Обмеження на змінні:

NJ-висновок повинен задовольняти ще таким умовам:

власна змінна

не повинна входити ні в формулу, позначену в схемі посредствомxFx. ні в одне з припущень, від яких ця формула залежить;

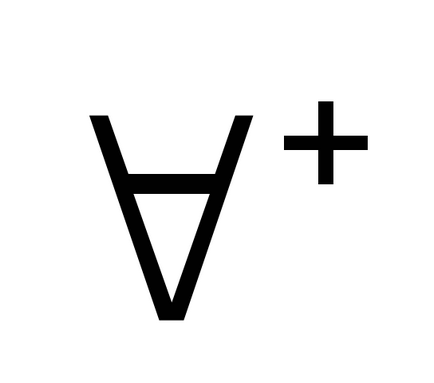
власна змінна

не повинна входити ні в формулу, позначену в схемі посредствомxFx ні в верхню формулу, позначену посредствомС. ні в одне з припущень, від яких остання залежить, виключаючи допущення, яке позначено посредствомFa і зіставлено даної фігурі ув'язнення.

Пояснення до схем фігур укладення та

Змістовний сенс ni-фігур ув'язнення.

Згідно Генценом, основна ідея створення натурального обчислення пов'язана з наміром "побудувати такий формалізм, який був би якомога ближче до применяющимся насправді міркувань".

Генцен вважав, що основною ознакою, що відрізняє натуральні обчислення від інших, зокрема аксіоматичних, є те, що "натуральні висновки виходять взагалі не з логічних аксіом, а з припущень, з яких робляться логічні висновки. А потім за допомогою деяких подальших висновків результат робиться вже незалежним від припущень ".

Зауважимо, що в нашому переліку схем фігур укладення знаки, які стоять в квадратних дужках вживаються в такому значенні: формально рівні формули цього виду в будь-якій кількості (в тому числі і нульовому) можуть зіставлятися фігурі укладення в якості припущень. Вони, отже, повинні бути вихідними формулами виведення і перебувати в тих нитках висновки, до яких належить відповідна верхня формула фігури укладення (тобто та верхня формула, над якою в схемі стоять квадратні дужки; вона сама повинна бути припущенням).

Зазначене у висновку відповідність між даною Н-фігурою укладення та співставленим їй ув'язненням відзначено, наприклад, за допомогою загальної нумерації.

Тепер ми пояснимо змістовний сенс схем фігур укладення і тим самим спробуємо показати, що обчислення NI відтворює "дійсні міркування".

+. Словами це висновок можна висловити так: "Якщо мають місце два висказиваніяА верб. То має місце і складне висловлювання (А В)".

-. Якщо доведено (має місце) висказиваніеА В. то має місце висказиваніеА. або має місце висловлювання. Цей факт відбивається наявністю двох схем ув'язнення.

 +. Якщо доведено висказиваніеА або висловлювання. то має місце і висловлювання (А В), цей факт також відбивається наявністю двох схем ув'язнення.

 - (розбір випадків): Якщо доведено (А В), то можна вести доказ розбором випадків. Припустимо спочатку, що має їхніх місцях. і з нього виведемС. Якщо далі з пропозиції про те, що має місце. знову вивеліС. ТОС взагалі має місце вже незалежно від обох припущень.

 +. Еслів доведено з використанням допущеніяА. то (вже без цього допущення Іза следуетВ. т.е (А В)).

 -. Це правило є вже ізвестнийmodus ponens. Якщо доказаноА і доказаноА В. то має місце верб.

 +. Якщо з допущеніяА слід щось хибне (Л), Тоа не є істинною, тобто має местоА.

 -: А іА означає "протиріччя", а таке не може відповідати дійсності (закон протиріччя). Це формально відображено в фігурі укладення

, де знакЛ означає "протиріччя", "хибність".

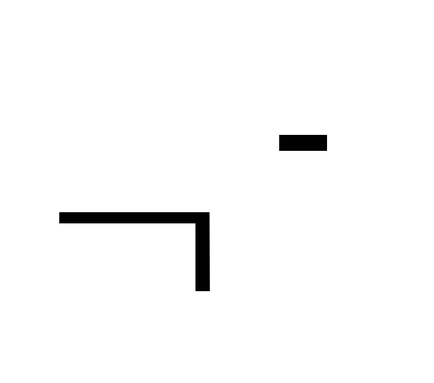
ВПВ: Якщо має місце щось хибне, то має місце будь-яке висловлювання.

 +. Якщо F доведено для будь-якого «для проізвольногоа», то має местоxFx. Припущення, чтоа «абсолютно довільно», може бути точніше виражено так: Fa не залежить ні від якого допущення, в яке входить предметна переменнаяа.

 -. Це правило абсолютно очевидно. Якщо доведено, що для всехх кожного класу має местоFx. то і для довільно вибранногоа з цього класу вірно, чтоFx

 +. ЕсліFa доведено «для проізвольногоа», то можна стверджувати, що існує «такойх, чтоFx;

 -. ІмеемxFx. Далі розмірковуємо так: нехай - саме такий об'єкт, для якого має местоF. тобто допустимо, що має местоFa. (В качествеу треба брати таку змінну, яка не входить вxFx. Якщо спираючись на це припущення, ми доведемо деякий висказиваніеС. Яке вже не содержіта і не залежить ні від яких інших припущень, содержащіха. ТОС доведено незалежно від допущеніяFa.

Введені позначення окремих фігур укладення показують, що є заслуговує на увагу систематизація їх. З кожним з логічних знаків , , , , , связана одна фігура "введення" і одна фігура «видалення» його як зовнішнього знака формули. Наявність двох фігур укладення - і + являє собою незначне чисто зовнішнє отклоненіе.Введенія є, так би мовити, "визначення" відповідних знаків, аудаленія є лише наслідками цих визначень. Це можна виразити таким чином: при видаленні певного знака формула, якої це стосується, і знак, про який йде мова, можуть використовуватися лише в тому значенні, яке вони отримують при введенні даного знака.

Наступні приклади могли б прояснити сказане: формула А В може бути введена, якщо є виводВ з допущеніяА. Застосовуючи ж потім до цієї формули удаленіе, ми діємо як раз таким чином, як ніби випливає з уже доказанногоА. а це випливає з того, чтоА В реєструє факт існування виводаВ Іза. Це можна представити у вигляді такої схеми:

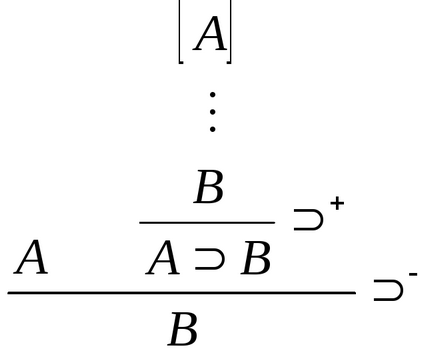
Приклад для кон'юнкції:

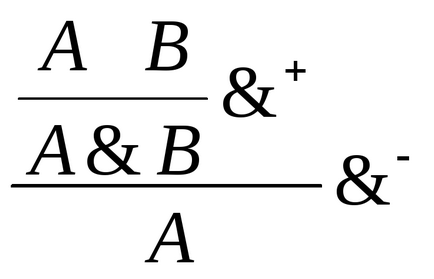
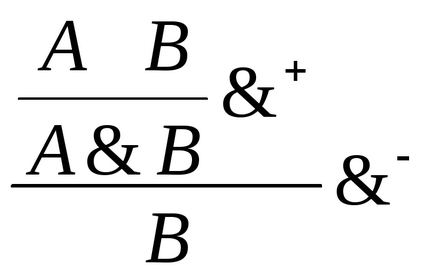
Вихідні формули А верб виходять двома кроками в результаті послідовного застосування правил + і -.

Із зазначеної систематизації фігур укладення випадає заперечення. Однак, заперечення можна виключити з нашого обчислення, якщо розглядати А як скорочення дляА Л. Це допустимо, тому що якщо в деякому NJ-виведення знищити все знакі, замінивши кожну формулу відаА формулойА Л. то вийде знову NJ-висновок (при цьому фігури заключенія + і - стануть приватними случаямі + і -), і назад: якщо в деякому NJ-виведення каждоеА Л замінити наА. то вийде знову NJ-висновок.

Схема фігур укладення ВПВ займає серед схем особливе місце, вона відноситься не до логічного знаку, а до знаку висказиваніяЛ.