визначення
Дерево відрізків - структура даних, що дозволяє виконувати багато операцій з відрізками масиву за $ O (\ log N) $. Дерево відрізків - універсальна структура даних, для якої можна реалізувати необмежений набір операцій (іноді за більшу складність: $ O (\ log ^ 2 N) $). Найпростіша версія дерева відрізків дозволяє знаходити суму або мінімум на відрізку, і змінювати окремі елементи.
Побудова дерева відрізків
Дерево відрізків - повне бінарне дерево, в якому кожна вершина відповідає за певний відрізок в масиві. Корінь дерева відповідає за весь масив, його дві дочірніх вершини - за дві половини, і так далі. У кожної вершини, що відповідає за відрізок довжиною більше $ 1 $, є дві дочірніх вершини, що відповідають за ліву і праву половини цього відрізка. Листя дерева відрізків відповідають за окремі елементи (відрізки довжиною $ 1 $).
Графічно це виглядає наступним чином (для масиву з 8 елементів):
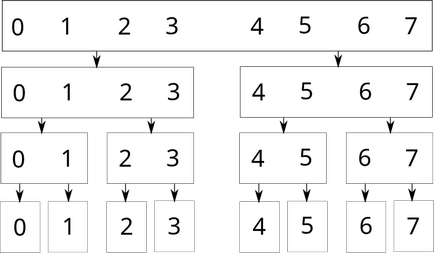
Кожен прямокутник - вершина дерева відрізків. Якщо деяка вершина відповідає за відрізок непарної довжини, то одна з її дочірніх вершин відповідатиме за відрізок довжиною $ \ lceil \ rceil $, а інша - за відрізок довжиною $ \ lfloor \ rfloor $. Наприклад, так виглядає дерево відрізків для масиву з 13 елементів:

Для масиву з $ n $ елементів дерево відрізків має близько $ 2n $ вершин ($ n + + + \ ldots $), а його висота дорівнює близько $ \ log n $.
Головне властивість дерева відрізків, на якому і будуються всі алгоритми роботи з ним: будь-який безперервний відрізок в масиві з $ n $ елементів можна представити за допомогою близько $ 2 \ log n $ вершин в дереві відрізків.
Наприклад, відрізок $ [1; 11] $ в масиві довжиною $ 13 $ можна уявити за допомогою наступних вершин:
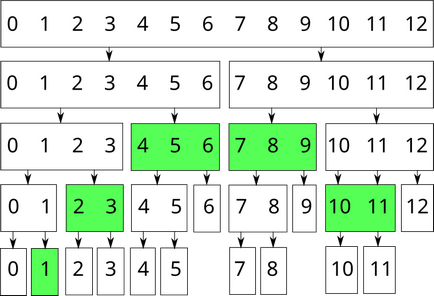
Дерево відрізків для пошуку суми
Одна з найпростіших функцій, яку можна вважати за $ O (\ log N) $ за допомогою дерева відрізків - сума.
При побудові дерева в кожній його вершині збережемо суму на відповідному відрізку (побудова буде вестися рекурсивно, тому досить просто скласти суми на двох дочірніх відрізках). Потім кожен запит суми на відрізку будемо розбивати на $ 2 \ log N $ відрізків, і знаходити суму на кожному з них за $ O (1) $, використовуючи предпросчітанние значення. Таким чином складність запиту суми дорівнює $ O (\ log N) $.
Крім запитів суми до дерева відрізків також можуть надходити запити на зміну окремих елементів (модифікацію). Зауважимо, що від зміни одного елемента значення суми зміниться в одній вершині на кожному рівні дерева відрізків (в яку входить цей елемент). Перерахуємо значення суми (знову ж, рекурсивно) тільки в цих вершинах. Таким чином складність запиту модифікації дорівнює висоті дерева, або $ O (\ log N) $.
Для реалізації запиту суми і запиту модифікації обхід дерева реалізується за допомогою одного і того ж алгоритму, заснованого на DFS. Нехай кордону нашого запиту $ [L; R] $ (в разі запиту модифікації $ L = R $), а кордони відрізка, відповідного поточної вершині $ [TL; TR] $. Залежно від взаємного положення цих кордонів, існують три варіанти дій алгоритму:
Поточний відрізок повністю входить в запит ($ L \ le TL; TR \ le R $).
Якщо це запит суми, повернемо предпросчітанную суму на відрізку. Якщо це запит модифікації, змінимо елемент і перерахуємо суму. В дочірні вершини спускатися немає потреби.
Поточний відрізок повністю не входить в запит ($ TR Ніяких дій виконувати не потрібно, просто вийдемо з функції. Якщо це запит суми, просто повернемо $ 0 $. Поточний відрізок частково входить в запит. Викличемо функцію рекурсивно для двох дочірніх відрізків. Якщо це запит суми, повернемо суму двох отриманих значень. Якщо це запит модифікації, перерахуємо значення суми для поточного відрізка (так як воно могло змінитися). Позначимо ці варіанти відповідно зеленим, червоним і жовтим кольором. Тоді запит суми на відрізку $ [1; 11] $ масиву довжиною $ 13 $ буде оброблений таким чином: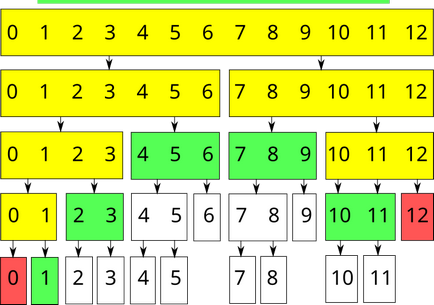
А запит модифікації $ 4 $ -го елемента:
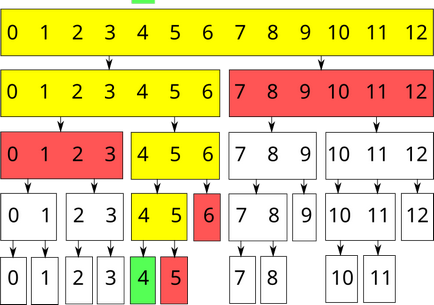
Реалізація дерева відрізків для пошуку суми
Повний бінарне дерево представляємо, як і в лекції про купу, за допомогою масиву і формул переходу $ l = 2v $ і $ r = 2v + 1 $. Для запобігання всіх можливих переповнень розмір дерева відрізків для масиву з $ n $ елементів приймають рівним $ 4n $.
Реалізація на C ++:
Реалізація дерева відрізків для пошуку мінімуму
Для пошуку мінімуму потрібно змінити в попередньої реалізації всього лише кілька рядків:
Дерева відрізків, що зберігають всі елементи
Для вирішення деяких завдань вершина, що відповідає за відрізок, повинна зберігати всі елементи цього відрізка в порядку сортування. Може здатися, що це займе дуже багато пам'яті, але це не так. Кожен елемент масиву зберігається один раз на кожному рівні дерева, яких $ \ log n $. Значить, вся структура даних займає $ O (N \ log N) $ пам'яті.
Класичною завданням на дерево відрізків такого виду є наступна:
Дан масив з $ N $ чисел, до якого надходить $ M $ запитів. Запити мають вигляд $ (l, r, x) $. На кожен запит потрібно відповісти, скільки елементів, більше або рівних $ x $, міститься на відрізку $ [l; r] $.
Для вирішення цього завдання будемо в кожній вершині дерева відрізків зберігати відсортоване std :: vector. що містить всі елементи відповідного відрізка. Для відповіді на запит будемо використовувати функцію std :: lower_bound. Вона дозволяє відповідати на запит для однієї вершини за $ O (\ log N) $, тому загальна складність відповіді на запит буде дорівнює $ O (\ log ^ 2 N) $.
Реалізація на C ++:
Якщо в подібних завданнях допускається модифікація елементів, то замість std :: vector потрібно зберігати std :: multiset. який дозволяє швидко видаляти і додавати елементи. Але в такому випадку ми вже не зможемо відповідати на запити кількості елементів, так як ітератори std :: multiset не можна віднімати один від одного.
Дерево відрізків з масовим оновленням. неузгоджені піддерева
Завдяки певній модифікації, дерево відрізків може виконувати оновлення елементів (збільшення або присвоювання) на відрізках довільної довжини за $ O (\ log N) $. Ця модифікація досить загальна, і дозволяє вирішувати за допомогою дерева відрізків цілий клас нових задач.
Ідея полягає в наступному. Нехай в процесі виконання запиту присвоювання на відрізку ми спустилися в вершину, повністю належить цьому відрізку. За логікою нам потрібно змінити значення в цій вершині, і у всіх вершинах її поддерева. Але складність такої операції неприйнятно висока: $ O (N \ log N) $.
Замість цього ми чинимо наступним чином: змінюємо значення тільки в самій вершині, без оновлення її поддерево (таким чином, в поддереве тепер зберігаються застарілі некоректні значення), і запам'ятовуємо, що у цієї вершини є неузгоджена модифікація. На цьому виконання запиту для вершини і її поддерева завершено.
Якщо наступні запитом не будуть звертатися до Піддерево з неузгодженою модифікацією, то вони будуть виконуватися коректно. Але рано чи пізно може надійти запит, який потрібно обробити індивідуально для дочірніх вершин з неузгодженою модифікацією. В цьому випадку ми чинимо просто: передамо модифікацію дочірнім вершин (тільки дочірнім вершин, а не всьому Піддерево). Тепер дана вершина узгоджена, а неузгодженість перейшла до її дочірнім. Така операція називається проштовхуванням модифікації.
Можливо, для обробки запиту були потрібні тільки дочірні вершини, і одного проштовхування вистачить. Якщо ж запит буде опускатися нижче за Піддерево, у міру його спуску будемо проштовхувати модифікацію все нижче і нижче. Проштовхування виконується за $ O (1) $ одночасно з поділом запиту, тому на асимптотику це ніяк не вплине.
Для прикладу, нехай ми працюємо з деревом відрізків для пошуку суми з масовим привласненням. Ми присвоїли відрізку $ [0; 6] $ значення $ x $. Змінимо значення суми в вершині, що відповідає за цей відрізок (встановимо його рівним $ 7x $), і встановимо для цієї вершини параметр неузгодженою модифікації рівним $ x $.
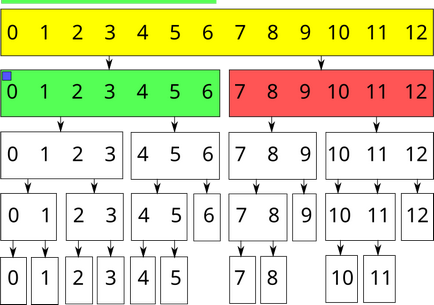
Синій квадрат позначає наявність у вершини неузгодженою модифікації.
Тепер опрацюємо запит знаходження суми на відрізку $ [6; 7] $:
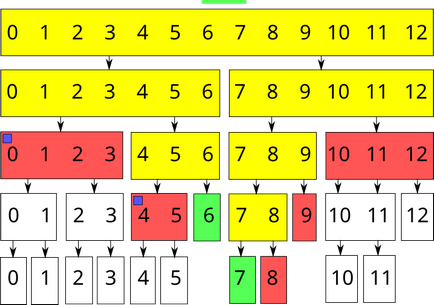
Як бачите, неузгодженість перейшла до відрізків $ [0; 3] $ і $ [4; 5] $. Вона перейшла б і до відрізка $ [6; 6] $, але у нього немає дочірніх вершин, тому неузгодженість усувається.