Тема даного поста - не нова, але, напевно, комусь стане в нагоді :) Почнемо з прикладу завдання, в якій використовується дерево відрізків.
Є масив з n (n≤10 ^ 5) цілих чисел, потрібно знаходити суму на відрізку від l до r (0≤l, r≤n-1) і змінювати значення i-го
(0≤i≤n-1) елемента. Кількість запитів m (m≤10 ^ 5).
Очевидно, що наївне рішення працює за O (n * m), а дерево відрізків дає можливість вирішувати це завдання з асимптотикою O (m * log2n).
Існує безліч різних видів дерев відрізків. У даній статті дерево відрізків - структура даних, яка за наявною послідовності з n чисел вміє виконувати швидко (за логарифмічна час) 2 види запитів:
1) Змінити значення i-го елемента
2) Обчислити значення деякої фіксованої асоціативної функції на відрізку від l до r.
Що ж собою являє дерево відрізків (ДО)? ДО - бінарне дерево (зазвичай, для зручності доповнюють до повного нульовими елементами), в якому листям є елементи вихідного масиву, а в кожній вершині записано значення функції f від двох синів. Тобто в листах записано значення функції на відрізку довжиною 1, в батьку записано значення функції на відрізку довжини 2, в батьку якого - 4 ... таким чином, в кожній вершині записано значення функції на деякому відрізку, що і послужило приводом для такої назви.
Для нашого прикладу завдання функція f - сума, тоді ДО для чотирьох елементів буде виглядати наступним чином:
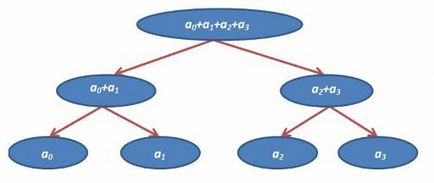
Якщо ж у нас кількість елементів (n) не є ступенем двійки, то ми доповнимо їх нулями. (В загальному випадку, коли ми працює з типом даних Т і функцією f, то нуль - таке значення, що для будь-якого x з T вірно f (x, нуль) = x.) Наприклад, ДО сум для 3 елементів буде виглядати так:
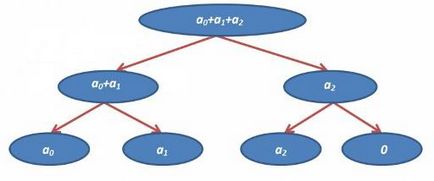
Як же зберігати ДО? Існує 2 способи:
• структури на покажчиках;
• лінійний масив.
На скільки мені відомо, перший спосіб використовують лише для персистентних ДО. Ми ж поки розбираємо саму звичайну і просту модифікацію ДО, тому скористаємося другим способом. Створимо лінійний масив a з 2 * nMax елементів, де nMax - найменший ступінь двійки, яка не перевищує n. У першому елементі (a [1]) будемо зберігати корінь дерева, а для кожної вершини i її сини зберігаються в осередках з номерами 2 * i (лівий син), 2 * i + 1 (правий син). Чому для зберігання досить 2 * nMax елементів? Ми маємо nMax листів, у них nMax / 2 батьків, у них nMax / 4 ... і 1 корінь, очевидно, що ця сума (1 + 2 + 4 + ... + nMax / 4 + nMax / 2 + nMax) дорівнює 2 * nMax -1.
На малюнку проставимо біля кожної вершини її індекс в масиві:
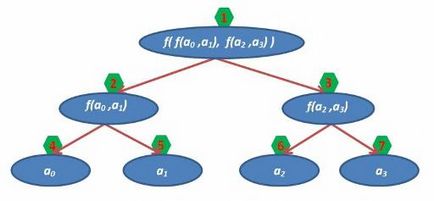
А в масив дерево буде укладено в такий спосіб:
Тепер визначимо, які операції ми хочемо виконувати з нашим ДО:
1) побудувати ДО;
2) дізнатися значення i-го елемента;
3) змінити значення i-го елемента;
4) знайти значення функції на відрізку від l до r.
Розберемо по черзі всі операції.
1 Побудувати дерево відрізків.
Нехай у нас є масив b з n елементів. Для початку нам потрібно знайти nMax (найменший ступінь двійки, яка не перевищує n). Це можна реалізувати як через формулу:
так і простеньким циклом:
Далі потрібно заповнити масив a нулями (відповідного типу) і заповнити листи ДО значеннями з масиву b (ми пам'ятаємо, що в ДО індекси листя від nMax до 2 * nMax-1):
На даний момент маємо:
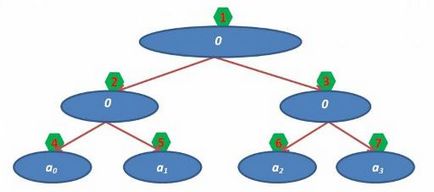
Тепер залишилося тільки заповнити значення у всіх батьків. Це можна зробити за один лінійний прохід (пам'ятаємо, що у i-ї вершини сини з індексами 2 * i і 2 * i + 1, а в вершині ми зберігаємо значення функції від двох синів):
Таким чином ми побудували ДО з асимптотикою O (nMax) = O (n).
2 Дізнатися значення i-го елемента.
Як уже писалося раніше у нашого ДО листя мають індекси від nMax до 2 * nMax-1, тому значення i-го елемента елемента перебувати в осередку з індексом nMax + i: return a [nMax + i] Очевидно, що даний запит виконується за константу .
3 Змінити значення i-го елемента.
Якщо ми змінимо значення в листі дерева, то все значення на шляху до кореня від даного листа перестануть відповідати дійсності, тому їх потрібно перерахувати, в інших же залишаться коректні значення. Як відомо, глибина повного бінарного дерева з m вершин дорівнює log2m, тому ми повинні виконати дану операцію за логарифмічна час. Наприклад, змінимо a2 на a2 I:
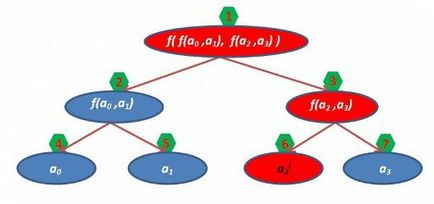
Червоним кольором виділені вершини, в яких потрібно змінити значення.
Що б «оновити» ДО нам потрібно записати в лист нового значення, а потім піднятися до кореня, кожен раз перераховуючи значення функції в вершині. Змінити значення в листі дуже просто (згадаємо, що індекси листя від nMax до 2 * nMax-1). Значення i-го листа має індекс nMax + i:
Тепер залишилося піднятися до кореня, це можна зробити за допомогою циклу:
4 Знайти значення функції на відрізку від l до r.
Нарешті, ми дісталися до самого цікавого запиту. Варто відзначити, що окремий випадок, коли l = r розібраний в пункті 2 і виконується за константу, в загальному ж випадку асимптотика логарифмічна.
Фундаментальний відрізок - такий відрізок, для якого існує вершина в дереві, що зберігає значення функції на даному відрізку.
Рівень. Рівень кореня - 1, а для кожного сина рівень на одиницю більше, ніж у батька.
Для того, що б обчислити значення функції на відрізку, нам необхідно розбити його на МІНІМАЛЬНА кількість фундаментальних відрізків. Що б знайти значення для будь-якої вершини (крім листа), нам потрібно знати значення для синів. Ми будемо спускатися по ДО. Спочатку встаємо в корінь. Нехай ми знаходимося в якійсь вершині. Розглянемо 3 можливих випадки: відрізок [l..r] збігається з відрізком, відповідним поточній вершині, відрізок [l..r] повністю належить одному з синів, відрізок належить обом синам. У першому випадку просто повертаємо пораховані значення з ДО, по-другому - спускаємося в даного сина, в-третьому ж випадку розіб'ємо даний відрізок на два: [l..правий кінець лівого сина] і [лівий кінець правого сина..r]. Рекурсивно обчислимо значення для кожного з них.
Розглянемо на прикладі. Нехай у нас є ДО для 8 елементів, запишемо, який відрізок відповідає кожній вершині:
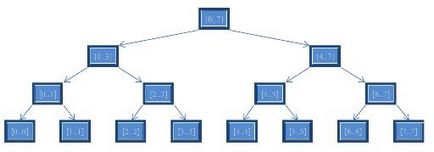
А тепер подивимося, як буде виконуватися запит для відрізка [1..5].
Спочатку встаємо в корінь - наш відрізок належить обом синам. Значить, нам потрібно розбити його на 2 відрізка: [1..3] і [4..5]. Для кожного з них рекурсивно обчислити значення. Далі відрізок [1..3] знову належить 2 синам, розбиваємо його на 2 відрізка: [1..1] і [2..3]. Відрізок [1..1] належить тільки правому синові, спускаємося в нього і бачимо, що відрізок [1..1] - фундаментальний. Беремо для нього значення з вершини, і піднімаємося до 2 рівня (вершина [0..3]). Для лівого сина ми вже рекурсивно порахували, тепер порахуємо для правого: спускаємося в нього. Відрізок [2..3] - фундаментальний, беремо значення з вершини. Повертаємося в [0..3] і вже можемо обчислити значення для відрізка [1..3], так як значення функції вже вирахували для обох його частин. Повертаємося в корінь і спускаємося в правого сина [4..7], наш подотрезок ([4..5]) належить тільки одному лівому синові, спускаємося в нього. Вершині відповідає відрізок [4..5], отже, він - фундаментальний, беремо з вершини значення. Повертаємося в корінь і обчислюємо відповідь.
Чому цей запит виконатися за логарифмічна час? Як відомо, глибина (кількість рівнів) дерева з n вершин дорівнює log2n, крім того, стверджується, що на кожному рівні ми відвідаємо не більше 4 вершин, таким чином, ми відвідаємо O (log2n) вершин. Розглянемо код. Для обчислення значення на відрізку нам знадобиться викликати рекурсивну функцію від 5 аргументів, для зручності напишемо функцію, яка по 2 аргументів (межі відрізка для запиту) викликає функцію 5-й аргументів і повертає значення:
Тепер наша рекурсивна функція:
Мій код класу дерево відрізків одинична модифікація.
P.S. Буду радий конструктивних зауважень / пропозицій по написанню статті / коду
дерево відрізків. картинки. код. segment tree