Вектори в тривимірному просторі
Геометричним представленням вектора є спрямований відрізок прямої лінії, що показано на рис. 1. У кожного вектора є дві властивості: довжина (також звана модулем або нормою вектора) і напрям. Завдяки цьому вектори дуже зручні для моделювання фізичних величин, які характеризуються модулем і напрямком. Наприклад, в розділі 14 ми реалізуємо систему частинок. При цьому ми будемо використовувати вектори для моделювання швидкості і прискорення наших часток. З іншого боку, в тривимірній комп'ютерній графіці вектори часто використовуються тільки для моделювання напрямки. Наприклад, нам часто потрібно вказати напрямок поширення світлових променів, орієнтацію межі або напрямок камери, яка дивитиметься на тривимірний світ. Вектори забезпечують зручний механізм завдання напряму в тривимірному просторі.
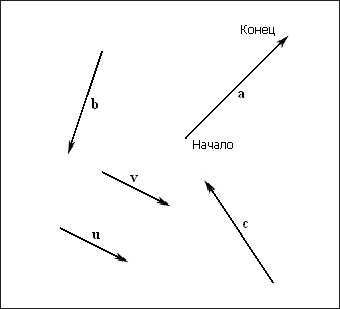
Мал. 1. Вільні вектори, певні незалежно від системи координат
Оскільки місце розташування не є характеристикою вектора, два вектора з однаковою довжиною і вказують в одному і тому ж напрямку вважаються рівними, навіть якщо вони розташовані в різних місцях. Зверніть увагу, що два таких вектора будуть паралельні один одному. Наприклад, на рис. 1 вектори u і v рівні.
На рис. 1 видно, що обсуждніе векторів може вестися без згадки системи координат, оскільки всю значиму інформацію, - довжину і напрямок, - вектор містить в собі. Додавання системи координат Не додає інформації в вектор; скоріше можна говорити, що вектор, значення якого є його невід'ємною частиною, просто описаний щодо конкретної системи координат. І якщо ми змінимо систему координат, ми тільки опишемо той же самий вектор щодо іншої системи.
Відзначивши цей важливий момент, ми перейдемо до вивчення того, як вектори описуються в лівосторонньої тривимірної декартової системі координат. На рис. 2 показані лівостороння і правостороння системи координат. Різниця між ними - позитивний напрямок осі Z. У лівосторонньої системі координат позитивний напрямок осі Z занурюється в сторінку. У правобічної системі координат позитивний напрямок осі Z направлено від сторінки.
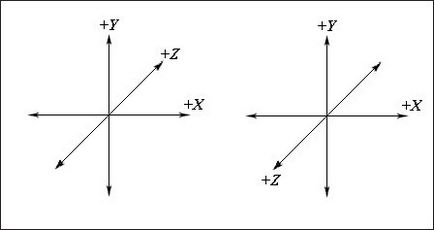
Мал. 2. Зліва зображена лівостороння система координат. Зверніть увагу, що позитивний напрямок осі Z направлено вглиб сторінки. Справа зображена правобічний система координат. Тут позитивний напрямок осі Z направлено від сторінки
Оскільки місце розташування вектора не змінює його властивостей, ми можемо перенести вектори таким чином, щоб початок кожного з них збігалося з початком координат обраної координатної системи. Коли початок вектора збігається з початком координат, кажуть, що вектор знаходиться в стандартній позиції. Таким чином, якщо вектор знаходиться в стандартній позиції, ми можемо описати його, вказавши тільки координати кінцевої точки. Ми будемо називати ці координати компонентами вектора. На рис. 3 показані вектори, зображені на рис. 1, які були переміщені в стандартні позиції.
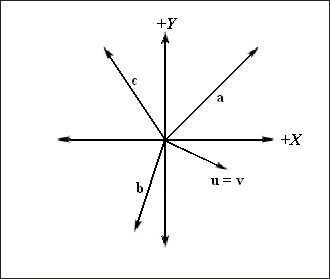
Мал. 3. Вектори в стандартній позиції, визначені у зазначеній системі координат. Зверніть увагу, що вектори u і v повністю збігаються один з одним тому що вони рівні
Оскільки ми описуємо знаходиться в стандартній позиції вектор, вказуючи його кінцеву точку, як якщо б ми описували окрему точку, легко переплутати точку і вектор. Щоб підкреслити відмінності між цими двома поняттями, ми знову наведемо визначення кожного з них. Точка описує тільки розташування в системі координат, в той час як вектор визначає величину і напрямок.
Ми будемо користуватися для позначення векторів напівжирними малими літерами, але іноді будемо застосовувати і напівжирний заголовні букви. Ось приклад двох-, трьох- і чотиривимірних векторів відповідно: u = (ux. Uy), N = (Nx. Ny. Nz), c = (cx. Cy. Cz. Cw).
Тепер ми введемо чотири спеціальних тривимірних вектора, які показані на рис. 4. Перший з них називається нульовим вектором. і значення всіх його компонент дорівнюють нулю; ми будемо позначати такий вектор виділеним напівжирним шрифтом нулем: 0 = (0, 0, 0). Наступні три спеціальних вектора називаються одиничними базовими векторами (базовими ортами) тривимірної системи координат. Ці вектори, спрямовані вздовж осей X, Y і Z нашої координатної системи, ми будемо називати i. j і k відповідно. Модуль цих векторів дорівнює одиниці, а визначення виглядає наступним чином: i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1).
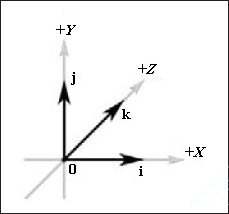
Мал. 4. Нульовий вектор і базові орт тривимірної системи координат
Вектор, довжина якого дорівнює одиниці, називається одиничним вектором або ортом.
У бібліотеці D3DX для подання векторів в тривимірному просторі ми можемо скористатися класом D3DXVECTOR3. Його визначення виглядає наступним чином:
Зверніть увагу, що D3DXVECTOR3 успадковує компоненти від D3DVECTOR. визначення якого виглядає наступним чином:
Так само, як і у скалярних величин, у векторів є власна арифметика, що видно з наявності описів математичних операцій у визначенні класу D3DXVECTOR3. Можливо, зараз ви не знаєте, що роблять ці методи. У наступних підрозділах ми розглянемо ці операції з векторами, інші допоміжні функції роботи з векторами з бібліотеки D3DX і деякі важливі особливості обробки векторів.
Хоча основний інтерес для нас представляють вектори в тривимірному просторі, займаючись програмуванням тривимірної графіки ми будемо іноді стикатися з векторами в двомірному і чотиривимірному просторах. Бібліотека D3DX надає класи D3DXVECTOR2 і D3DXVECTOR4. призначені для подання векторів в двомірному і чотиривимірному просторах відповідно. Вектори в просторах з іншою кількістю вимірювань мають ті ж властивості, що й вектори в тривимірному просторі, а саме - довжиною і напрямком, відрізняється тільки кількість вимірювань. Крім того, математичні операції з векторами, за винятком векторного твори (див. Розділ «Векторне твір», далі в цій главі), яке визначено тільки для тривимірної системи координат, можуть бути узагальнені для векторів будь-якої розмірності. Таким чином, за винятком векторного твори, всі операції, які ми обговорюємо для векторів в тривимірному просторі, поширюються і на вектори в двомірному, чотиривимірному і навіть n-вимірному просторах.
рівність векторів
В геометрії два вектора вважаються рівними, якщо вони вказують в одному і тому ж напрямку і мають однакову довжину. В алгебрі кажуть, що вектори рівні, якщо у них однакова кількість вимірювань і їх відповідні компоненти рівні. Наприклад, (ux. Uy. Uz) = (vx. Vy. Vz) якщо ux = vx. uy = vy і uz = vz.
У коді ми можемо перевірити чи рівні два вектора, використовуючи перевантажений оператор рівності:
Аналогічним чином, можна переконатися, що два вектори не рівні, використовуючи перевантажений оператор нерівності:
Порівнюючи числа з плаваючою точкою слід бути дуже акуратним, оскільки через похибки округлення, два числа з плаваючою точкою, які повинні бути рівними, можуть злегка відрізнятися. З цієї причини ми перевіряємо приблизна рівність чисел з плаваючою точкою. Для цього ми визначили константу EPSILON. містить дуже маленьке значення, яке буде служити «буфером». Ми будемо говорити, що два числа приблизно рівні, якщо різниця між ними менше EPSILON. Іншими словами, EPSILON дає нам якийсь допуск для помилок округлення чисел з плаваючою точкою. Наведена нижче функція показує, як EPSILON може використовуватися при перевірці рівності двох чисел з плаваючою точкою: Про це не треба турбуватися, працюючи з класом D3DXVECTOR. оскільки перевантажені операції порівняння всі зроблять за нас, але дуже важливо знати про цю особливість порівняння чисел з плаваючою точкою.
Обчислення модуля вектора
В геометрії модулем вектора називається довжина спрямованого відрізка лінії. В алгебрі, знаючи компоненти вектора ми можемо обчислити його модуль за наступною формулою:
Вертикальні лінії в | u | позначають модуль u.
У коді для вирахування двох векторів ми будемо застосовувати перевантажених оператор віднімання:
Як видно на рис. 6, операція віднімання векторів повертає вектор, початок якого збігається з кінцем вектора v. а кінець - з кінцем вектора u. Якщо ми інтерпретуємо компоненти u і v як координати точок, то результатом вирахування буде вектор, спрямований від однієї точки до іншої. Це дуже зручна операція, оскільки нам часто буде необхідно знайти вектор, що описує напрямок від однієї точки до іншої.
Множення вектора на скаляр
Як видно з назви розділу, ми можемо множити вектор на скаляр, в результаті чого відбувається масштабування вектора. Якщо масштабний множник позитивний, напрямок вектора не змінюється. Якщо ж множник від'ємний, то напрямок вектора змінюється на протилежне (інвертується).
Клас D3DXVECTOR3 надає оператор множення вектора на скаляр:
Скалярний добуток векторів
Скалярний добуток векторів - це перша з двох визначених у векторній алгебрі операцій множення. Обчислюється такий твір наступним чином:
У наведеній вище формули немає очевидної геометричній інтерпретації. Використовуючи теорему косинусів 1. ми отримаємо відношення u Ч v = | u || v | cos j. говорить, що скалярний добуток двох векторів дорівнює добутку косинуса кута між векторами на модулі векторів. Отже, якщо u і v - одиничні вектори, їх скалярний добуток дорівнює косинусу кута між ними.
Ось деякі корисні властивості скалярного твори:
- Якщо u Ч v = 0, значить u ^ v.
- Якщо u Ч v> 0, значить кут j між двома векторами менше 90 градусів.
- Якщо u Ч v <0, значит угол j между двумя векторами больше 90 градусов.
Символ ^ позначає «прямокутний» або (що те ж саме) «перпендикулярний».
Для обчислення скалярного добутку двох векторів в бібліотеці D3DX призначена наступна функція:
Векторний витвір
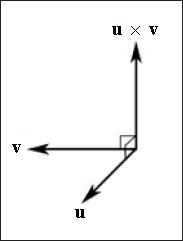
Другою формою операції множення, визначеної в векторній алгебрі, є векторний добуток. На відміну від скалярного твори, результатом якого є число, результатом векторного твори буде вектор. Векторним твором двох векторів u і v буде інший вектор, p. є взаємно перпендикулярним для векторів u і v. Це означає, що вектор p перпендикулярний вектору u і одночасно вектор p перпендикулярний вектору v.
Обчислюється векторний добуток за такою формулою:
У компонентної формі обчислення виглядає так:
Обчисліть j = k × i = (0, 0, 1) × (1, 0, 0) і перевірте, що вектор j перпендикулярний як вектору i. так і вектору k.
Таким чином, j = (0, 1, 0). Згадайте, в попередньому розділі «Скалярний добуток векторів» говорилося, що якщо u Ч v = 0, значить u ^ v. Оскільки j Ч k = 0 і j Ч i = 0, ми знаємо що вектор j перпендикулярний як вектору k. так і вектору i.
Для обчислення векторного добутку двох векторів в бібліотеці D3DX призначена наступна функція:
Як випливає з рис. 7, вектор -p також взаємно перпендикулярний векторах u і v. Який з векторів, p або -p буде повернений в якості результату векторного твори визначається порядком операндів. Іншими словами, u × v = - (v × u). Це заначіт, що операція векторного твори не є комутативність. Визначити, який вектор буде повернений в якості результату, можна за допомогою правила лівої руки. (Ми використовуємо правило лівої руки, оскільки працюємо з лівосторонньої системою координат. Якби у нас була правостороння система координат, довелося б скористатися правилом правої руки.) Якщо розташувати пальці лівої руки вздовж першого вектора, а долоню руки - уздовж другого, відігнутий на 90 градусів великий палець вкаже напрям результуючого вектора.
1 Теорема косинусів визначає залежність між сторонами і кутами трикутника. Вона стверджує, що у всякому трикутнику квадрат довжини сторони дорівнює сумі квадратів двох інших сторін без подвоєного твори довжин цих сторін на косинус кута між ними. Якщо кут прямий, то теорема косинусів переходить в теорему Піфагора, тому що косинус прямого кута дорівнює 0.