Дії над матрицею
1. Додавання і віднімання матриць:
Додавання і віднімання матриць - одне з найпростіших дій над ними, тому що необхідно скласти або відняти відповідні елементи двох матриць. Головне пам'ятати, що додавати і віднімати можна тільки матриці однакових розмірів. тобто тих, у яких однакова кількість рядків і однакову кількість стовпців.
Наприклад, нехай дано дві матриці рівного розміру 2х3, тобто з двома рядками і трьома стовпцями:
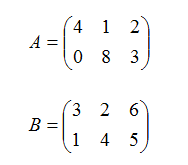
Сума двох матриць:
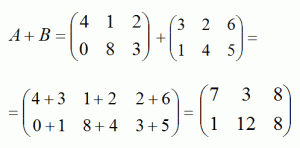
Різниця двох матриць:
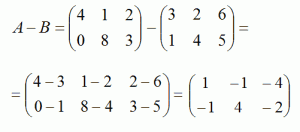
2. Множення матриці на число:
Множення матриці на число - процес, що полягає в множенні числа на кожен елемент матриці.
Наприклад, нехай дана матриця А:
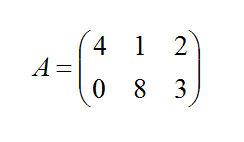
Помножимо число 3 на матрицю А:
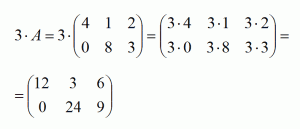
3. Множення двох матриць:
Множення двох матриць можливо тільки за умови, що число стовпців першої матриці має дорівнювати числу рядків другої. Нова матриця, яка вийде при множенні матриць, буде складатися з кількості рядків, що дорівнює кількості стовпців першої матриці і кількості стовпців, дорівнює кількості рядків другої матриці.
Припустимо є дві матриці розмірами 3х4 і 4х2, тобто в першій матриці 3 рядки і 4 шпальти, а в другій матриці 4 рядки і 2 колонки. Оскільки кількість стовпців першої матриці (4), дорівнює кількості рядків другої матриці (4), то матриці можна перемножити, нова матриця буде мати розмір: 3х2, тобто 3 рядки і 2 колонки.
Можна уявити все це у вигляді схеми:
Після того як Ви визначилися з розміром нової матриці, яка вийде при множенні двох матриць, можна приступити до заповнення цієї матриці елементами. Якщо Вам треба заповнити першу сходинку першого стовпчика цієї матриці, то треба кожен елемент першого рядка першої матриці множити на кожен елемент першого стовпця другого матриці, якщо будемо заповнювати другий рядок першого стовпця відповідно будемо брати кожен елемент другого рядка першої матриці і множити на перший стовпець другий матриці і т.д.
Подивимося як це виглядає на схемі:
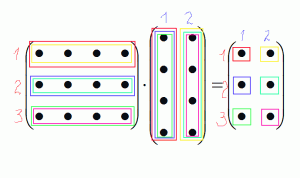
Подивимося як це виглядає на прикладі:
Дано дві матриці:
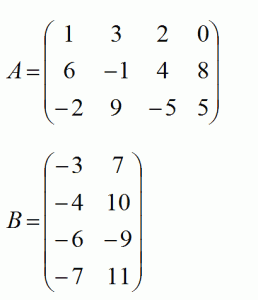
Знайдемо добуток цих матриць:
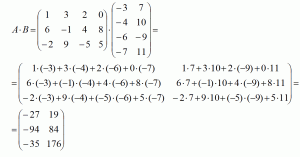
4. Розподіл матриць:
Розподіл матриць - дія над матрицями, яке в цьому понятті не зустрінеш в підручниках. Але якщо є необхідність розділити матрицю А на матрицю В, то в цьому випадку використовують одне з властивостей ступенів:
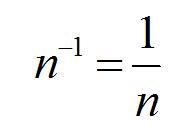
Згідно цій властивості розділимо матрицю А на матрицю В:
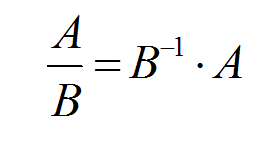
В результаті задача про розподіл матриць зводитися до множення зворотної матриці матриці В на матрицю А.
Нехай є квадратна матриця n-го порядку
Матриця А -1 називається оберненою матрицею по відношенню до матриці А, якщо А * А -1 = Е, де Е - одинична матриця n-го порядку.
Одинична матриця - така квадратна матриця, у якої всі елементи по головній діагоналі, що проходить від лівого верхнього кута до правого нижнього кута, - одиниці, а решта - нулі, наприклад:
Зворотній матриця може існувати тільки для квадратних матриць тобто для тих матриць, у яких число рядків і стовпців збігаються.
Теорема умови існування оберненої матриці
Для того щоб матриця мала зворотний матрицю необхідно і достатньо, щоб вона була невироджених.
Матриця А = (А1, А2. Аn) називається невироджених. якщо вектори-стовпці є лінійно незалежними. Число лінійно незалежних векторів-стовпців матриці називається рангом матриці. Тому можна сказати, що для того, щоб існувала обернена матриця, необхідно і достатньо, щоб ранг матриці дорівнював її розмірності, тобто r = n.
Записати в таблицю для вирішення систем рівнянь методом Гаусса матрицю А і праворуч (на місце правих частин рівнянь) приписати до неї матрицю Е.
Використовуючи перетворення Жордана, привести матрицю А до матриці, що складається з одиничних стовпців; при цьому необхідно одночасно перетворити матрицю Е.
Якщо необхідно, то переставити рядки (рівняння) останньої таблиці так, щоб під матрицею А вихідної таблиці вийшла одинична матриця Е.
Записати зворотну матрицю А -1. яка знаходиться в останній таблиці під матрицею Е вихідної таблиці.
Для матриці А знайти зворотну матрицю А -1
Рішення: Записуємо матрицю А і праворуч приписуємо одиничну матрицю Е. Використовуючи перетворення Жордана, наводимо матрицю А до одиничної матриці Є. Обчислення приведені в таблиці 31.1.
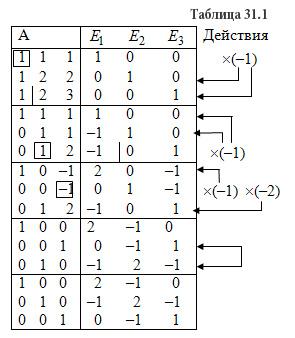
Перевіримо правильність обчислень множенням вихідної матриці А і оберненої матриці А-1.
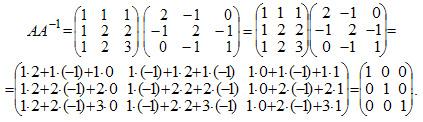
В результаті множення матриць вийшла одинична матриця. Отже, обчислення зроблені правильно.
Визначники матриць (Детермінанти) Визначники матриць (Детермінанти)
Визначники матриць, спосіб № 1:
Визначником квадратної матриці (det A) називається число, яке може бути обчислено за елементами матриці за формулою:
де М1k - визначник матриці (детермінант), отриманої з вихідної матриці викреслюванням першого рядка і k - oго стовпчика. Слід звернути увагу на те, чтоопределітелі мають тільки квадратні матриці. тобто матриці, у яких число рядків дорівнює числу стовпців. Перша формула дозволяє обчислити визначник матриці по першому рядку, також справедлива формула обчислення визначника матриці по на одну:
Взагалі кажучи, визначник матриці може обчислюватися по будь-якому рядку або столбцуматріци. тобто справедлива формула:
Очевидно, що різні матриці можуть мати однакові визначники. Визначник одиничної матриці дорівнює 1. Для зазначеної матриці А число М1k називається додатковим мінор елемента матриці a1k. Таким чином, можна зробити висновок, що кожен елемент матриці має свій додатковий мінор. Додаткові мінори існують тільки в квадратних матрицях.
Додатковий мінор довільного елемента квадратної матриці aij равенопределітелю матриці. отриманої з вихідної матриці викреслюванням i-го рядка і j-го стовпця.
Визначники матриць, спосіб № 2:
Визначником матриці першого порядку, або визначником першого порядку, називається елемент а11:
Визначником матриці другого порядку, або визначником другого порядку, називається число, яке обчислюється за формулою:
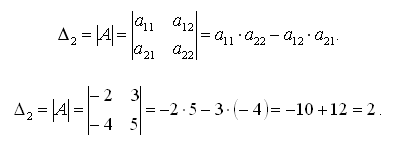
Визначником матриці третього порядку, або визначником третього порядку, називається число, яке обчислюється за формулою:
Це число являє алгебраїчну суму, що складається з шести доданків. У кожний доданок входить рівно по одному елементу з кожного рядка і кожного стовпця матриці. Кожне складова складається з добутку трьох співмножників.

Знаки, з якими члени визначника матриці входять в формулу знаходження визначника матриці третього порядку можна визначити, користуючись наведеною схемою, яка називається правилом трикутників або правилом Сарруса. Перші три складові беруться зі знаком плюс і визначаються з лівого малюнка, а наступні три складові беруться зі знаком мінус і визначаються з правого малюнка.
Обчислення визначників матриць четвертого і більш високого порядку призводить до великих обчислень, так як:
для знаходження визначника матриці першого порядку ми знаходимо один доданок, що складається з одного сомножителя;
для знаходження визначника матриці другого порядку потрібно обчислити алгебраїчну суму з двох доданків, де кожний доданок складається з добутку двох співмножників;
для знаходження визначника матриці третього порядку потрібно обчислити алгебраїчну суму з шести доданків, де кожний доданок складається з добутку трьох співмножників;
для знаходження визначника матриці четвертого порядку потрібно обчислити алгебраїчну суму з двадцяти чотирьох доданків, де кожний доданок складається з твору чотирьох співмножників і т.д.
Визначити кількість доданків, для знаходження визначника матриці. в сумі алгебри, можна обчисливши факторіал: 1! = 1 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6 4! = 1 × 2 × 3 × 4 = 24 5! = 1 × 2 × 3 × 4 × 5 = 120.