7 Раб

Дії над комплексними числами в алгебраїчній і тригонометричної формі.

Поняття комплексного числа і його геометрична інтерпретація.

Дії над комплексними числами в алгебраїчній формі.

Тригонометрична форма комплексного числа.

Дії над комплексними числами в тригонометричної формі.

1. Поняття комплексного числа і його геометрична інтерпретація.

Визначення 1. Комплексними числами називаються числа виду

, деі- дійсні числа, а число, визначається рівністю, називається уявною одиницею, якщо для цих чисел поняття рівності і дії додавання і множення визначені в такий спосіб:

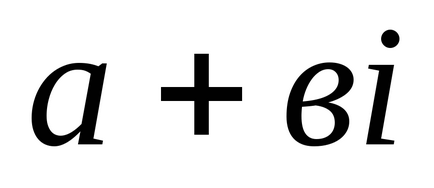
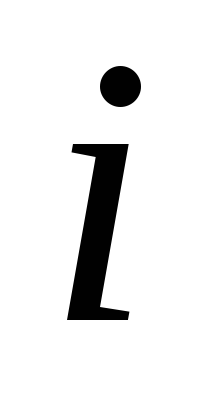
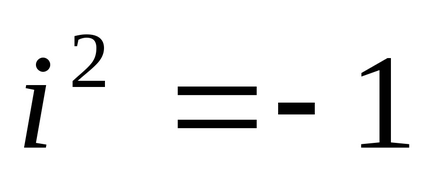
1). Два комплексних числа

іназиваються рівними, якщо,;

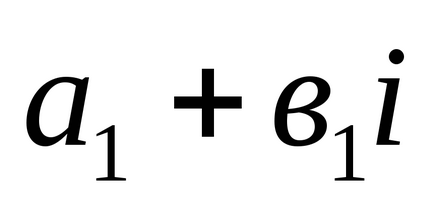
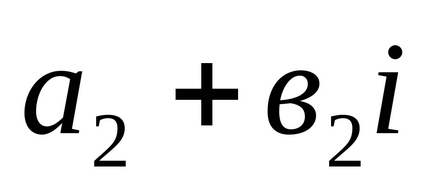
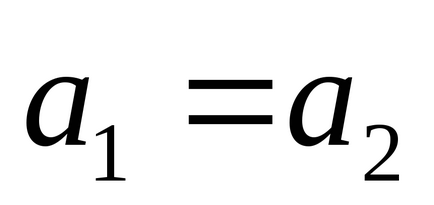
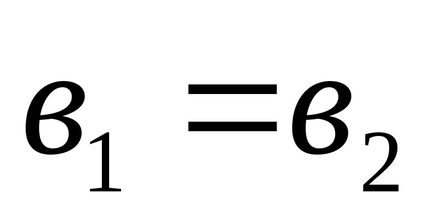
2). Сумою двох комплексних чисел

іназивається комплексне число;

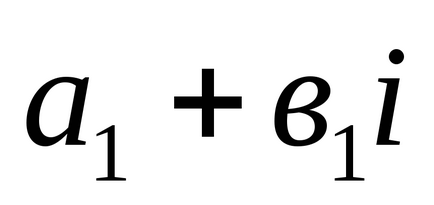
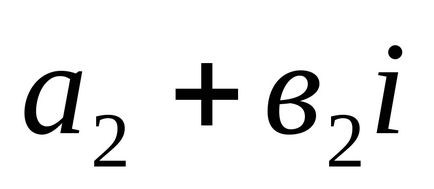
3). Твором двох комплексних чисел

іназивається комплексне число;

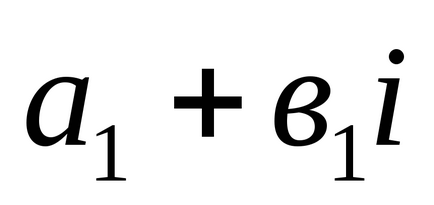
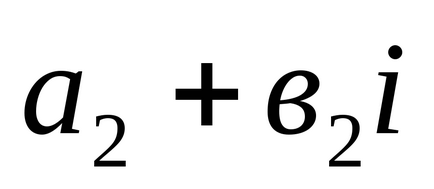
Запис комплексного числа у вигляді

називаетсяалгебраіческой формойзапісі комплексного числа, деназиваетсядействітельной частьюкомплексного числа, а-уявною частиною.

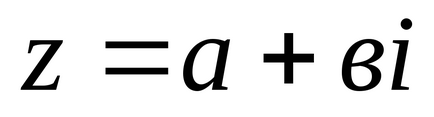
Будь-яке дійсне число міститься в безлічі комплексних чисел. Тому його можна записати так:

.

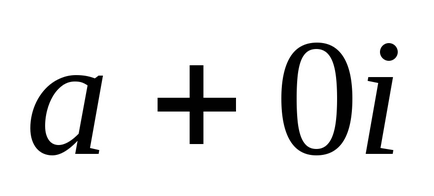
Визначення 2: Комплексне число

називаетсякомплексно зв'язаних

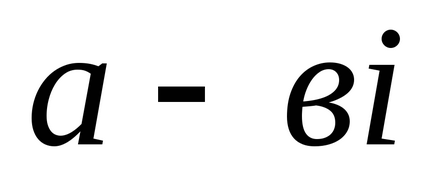
з числом

і позначається, тобто.

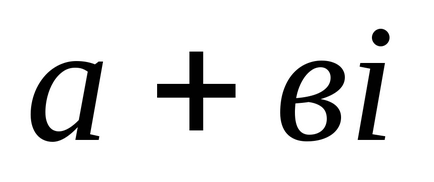
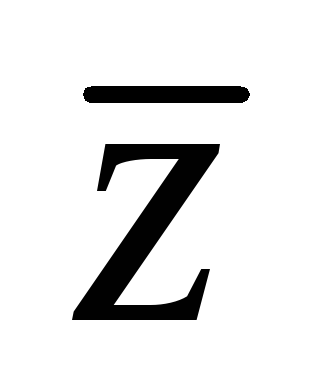
Визначення 3: Модулем комплексного числа

називається число





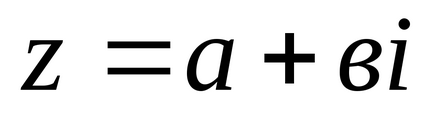
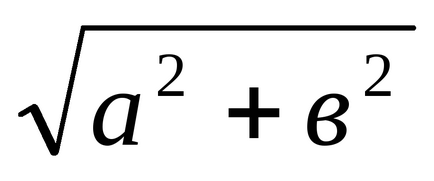
:. причому.

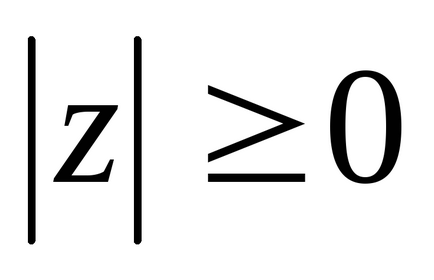
Комплексне число можна зобразити двома способами:

1. Точкою площині з координатами (а; в).

При цьому дійсні числа зображуються точками осі абсцис, яку називають дійсною віссю. а чисто уявні числа- точками осі ординат, яку називають уявною віссю.

2. У вигляді вектора з початком на початку координат (

) І кінцем в точці М (а; в) ().

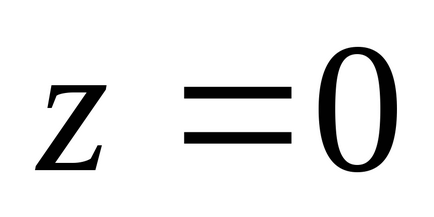
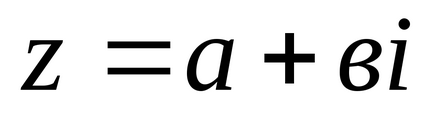
Кожній точці площини з координатами (а; в) відповідає один і тільки один вектор з початком у точці О (0; 0) і кінцем в точці М (а; в), тому комплексне число

можна зобразити у вигляді вектора.

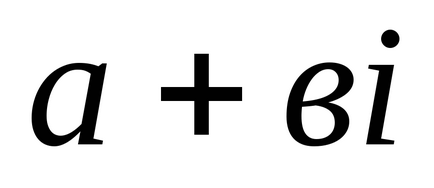
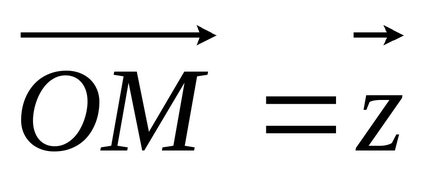
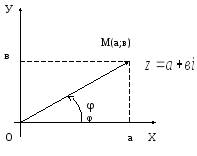
Визначення 4: Кут φ між дійсною віссю ОХ і вектором

, відлічуваний від позитивного напрямку дійсної осі, називаетсяаргументом комплексного числа. Якщо відлік ведеться проти руху годинникової стрілки, то величина кута вважається позитивної, інакше-негативною.

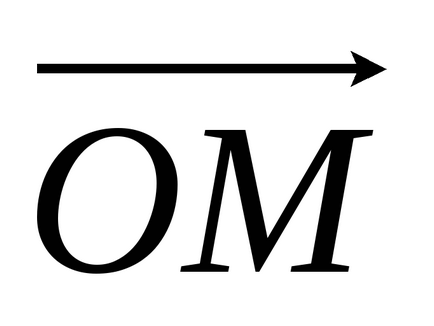
Будь-яке комплексне число має нескінченну безліч аргументів, що відрізняються один від одного на число, кратне

. Найменша за абсолютною величиною значення аргументу з промежутканазиваетсяглавним значенням аргументу.

З визначення тригонометричних функцій слід:

Зобразити геометричну інтерпретацію комплексного числа, знайти модуль комплексного числа і головне значення аргументу.

;

;

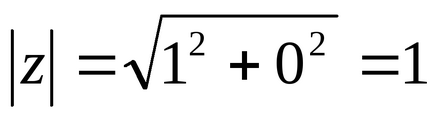
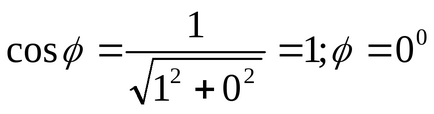
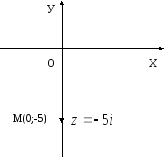
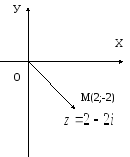
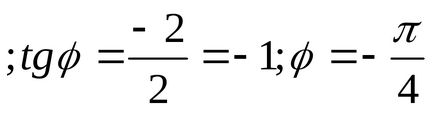
2. Дії над комплексними числами в алгебраїчній формі.

Додавання і множення комплексних чисел ми ввели в визначенні комплексного числа. Введемо правила віднімання і ділення комплексних чисел:;

.

Але найзручніше дії над комплексними числами проводити за допомогою правил відповідних дій над многочленами і поняттям уявної одиниці.

к). .

3. Тригонометрична форма комплексного числа.

Зобразимо комплексне число

геометрично:

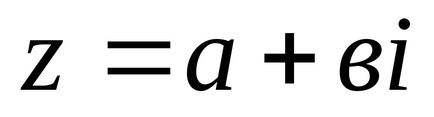
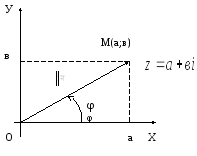
Позначимо модуль комплексного числа.

Аргументом комплексного числа називається кут φ, який обчислюється за допомогою формул:

Підставами отримані формули в

, отримаємо:

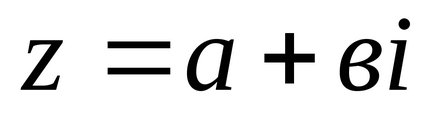
- тригонометрическая форма комплексного числа.

Алгоритм переходу з алгебри форми комплексного числа в тригонометричну:

Зобразити геометрично число

, для знаходження чверті числа φ.

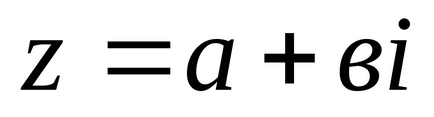
Скласти рівняння:

і знайти φ.

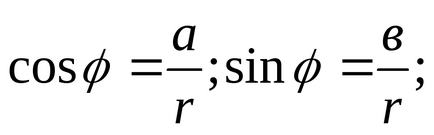
Записати z в тригонометричної формі.

Приклади: а) .Перевесті числа з алгебраїчної форми в тригонометричну.

2. Зобразимо геометрично:

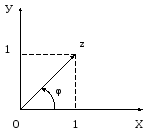
Значить φ належить I чверті.

2. Зобразимо геометрично:

, так як z належить позитивної півосі ОУ.

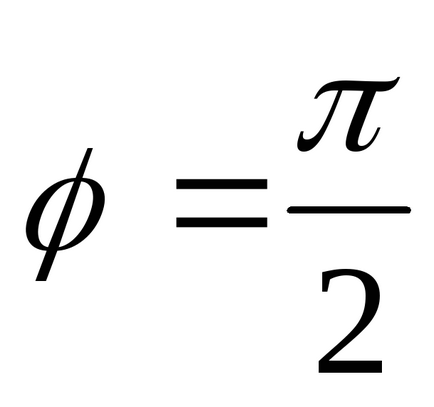
Значить 3 пункт можна опустити.

2. Зобразимо геометрично:

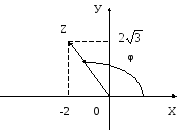
φ належить II чверті.

б). перевести з тригонометричної форми в алгебраїчну:

.

.

4. Дії над комплексними числами в тригонометричної формі.

Нехай дано два числа в тригонометричної формі: і.

1). При множенні двох комплексних чисел, заданих в тригонометричної формі, їх модулі перемножуються, а аргументи складаються:

.

2). При розподілі двох комплексних чисел, заданих в тригонометричної формі, їх модулі діляться, а аргументи віднімаються:

.

3). При зведенні комплексного числа Вn-ую ступінь використовується формула:

, яка називається формулою Муавра.

4). Для витягання кореня n-го ступеня з комплексного числа використовується формула:

.