Нагадаємо центральне визначення - визначення логарифма. Воно пов'язане з рішенням показового рівняння. Дане рівняння має єдиний корінь, його називають логарифмом b за основою а:
Логарифмом числа b по підставі а називається такий показник ступеня, в яку потрібно звести підставу а, щоб отримати число b.
Нагадаємо основне логарифмічна тотожність.
Вираз (вираз 1) є коренем рівняння (вираз 2). Підставами значення х з виразу 1 замість х в вираз 2 і отримаємо основне логарифмічна тотожність:
Отже ми бачимо, що кожному значенню ставиться у відповідність значення. Позначимо b за х (), з за у, і таким чином отримуємо логарифмічну функцію:
Згадаймо основні властивості логарифмічної функції.
Ще раз звернемо увагу, тут, т. К. Під логарифмом може стояти строго позитивне вираження, як підставу логарифма.
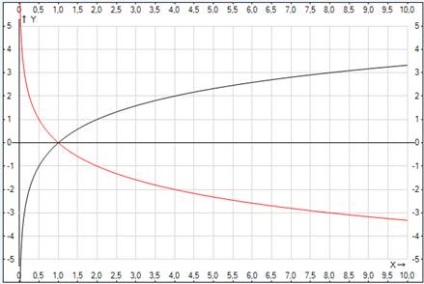
Мал. 1. Графік логарифмічної функції при різних підставах
Графік функції при зображений чорним кольором. Мал. 1. Якщо аргумент зростає від нуля до нескінченності, функція зростає від мінус до плюс нескінченності.
Графік функції при зображений червоним кольором. Мал. 1.
Властивості цієї функції:
Функція монотонна на всій своїй області визначення. При монотонно (строго) зростає, більшому значенню аргументу відповідає більше значення функції. При монотонно (строго) убуває, більшому значенню аргументу відповідає менше значення функції.
Властивості логарифмічної функції є ключем до вирішення різноманітних логарифмічних рівнянь.
Розглянемо найпростіше логарифмічне рівняння, всі інші логарифмічні рівняння, як правило, зводяться до такого виду.
Оскільки рівні підстави логарифмів і самі логарифми, рівні і функції, які стоять під логарифмом, але ми повинні не втратити область визначення. Під логарифмом може стояти тільки позитивне число, маємо:
Ми з'ясували, що функції f і g рівні, тому досить вибрати одне будь нерівність щоб дотримати ОДЗ.
Таким чином, ми отримали змішану систему, в якій є рівняння і нерівність:
Нерівність, як правило, вирішувати необов'язково, досить вирішити рівняння і знайдені коріння підставити в нерівність, таким чином виконати перевірку.
Сформулюємо метод вирішення найпростіших логарифмічних рівнянь:
Зрівняти підстави логарифмів;
Прирівняти подлогаріфміческіе функції;
Розглянемо конкретні приклади.
Приклад 1 - вирішити рівняння:
Підстави логарифмів спочатку рівні, маємо право прирівняти подлогаріфміческіе вираження, не забуваємо про ОДЗ, виберемо для складання нерівності перший логарифм:
Знайдемо корінь і підставимо його в нерівність:
Приклад 2 - вирішити рівняння:
Дане рівняння відрізняється від попереднього тим, що підстави логарифмів менше одиниці, але це ніяк не впливає на рішення:
Підстави логарифмів спочатку рівні, маємо право прирівняти подлогаріфміческіе вираження, не забуваємо про ОДЗ, виберемо для складання нерівності другий логарифм:
Знайдемо корінь і підставимо його в нерівність:
Отримали невірне нерівність, отже, знайдений корінь не задовольняє ОДЗ.
Приклад 3 - вирішити рівняння:
Підстави логарифмів спочатку рівні, маємо право прирівняти подлогаріфміческіе вираження, не забуваємо про ОДЗ, виберемо для складання нерівності другий логарифм:
Знайдемо корінь і підставимо його в нерівність:
Очевидно, що тільки перший корінь задовольняє ОДЗ.
Отже, ми приступили до вивчення важливої теми - рішення логарифмічних рівнянь. Ми розглянули методику рішення найпростіших рівнянь і кілька прикладів її застосування.