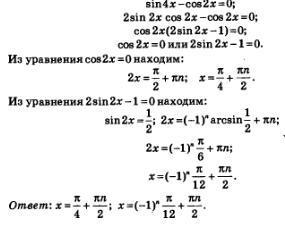Спектр застосування формул складання досить широкий. Ми не ставимо за мету перерахувати всі можливі варіанти застосування формул складання, тут ми лише подивимося, як застосовуються ці формули на практиці.
Для початку за допомогою однієї з формул додавання перевіримо формулу приведення виду. Скористаємося формулою синуса суми. Маємо. Так доведена формула.
Формули додавання дозволяють обчислювати точні значення синуса, косинуса, тангенса і котангенс деяких кутів, відмінних від основних (). Розглянемо рішення прикладу.
Обчисліть точне значення тангенса 15 градусів.
Легко помітити, що кут 15 градусів можна подати як різницю 45-30. Тоді формула тангенса різниці дозволить нам обчислити потрібну установку. За вказаною формулою отримуємо. Тепер підставляємо відомі значення тангенса, після чого завершуємо обчислення:

.
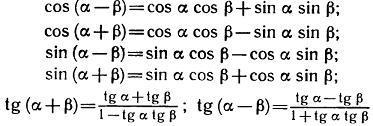
Наприклад, вам потрібно визначити синус, косинус, тангенс або котангенс будь-якого кута від 0 до 450 градусів:
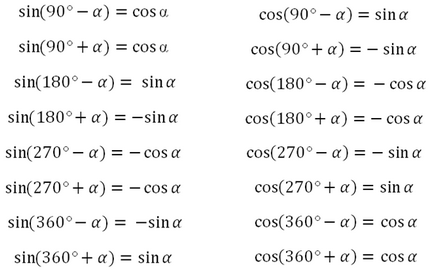
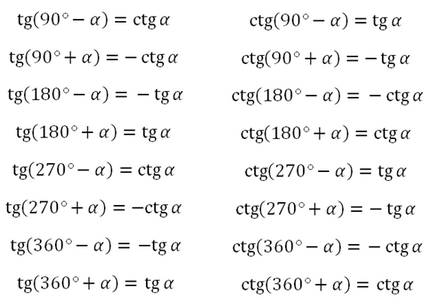
кут альфа лежить межах від 0 до 90 градусів
Отже, необхідно усвідомити «закон», який тут працює:
1. Визначте знак функції у відповідній чверті.
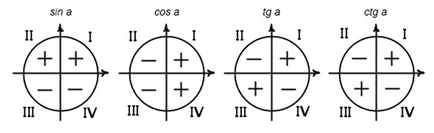
2. Запам'ятайте наступне:
функція змінюється на кофункцію
(Синус на косинус або навпаки, тангенс на котангенс або навпаки)
функція на кофункцію не змінюється
Тепер за представленим закону запишемо декілька формул приведення самостійно:
Даний кут лежить у третій чверті, косинус в третій чверті негативний. Функцію на кофункцію не змінюємо, так як у нас 180 градусів, значить:
Кут лежить у третій чверті, косинус в третій чверті негативний. Міняємо функцію на кофункцію, так як у нас 270 градусів, значить:
Кут лежить в першій чверті, синус в першій чверті позитивний. Чи не міняємо функцію на кофункцію, так як у нас 360 градусів, значить:
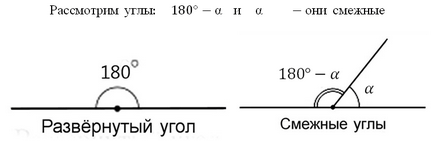
Ось вам ще додаткове підтвердження того, що синуси суміжних кутів рівні:
§ 24. Формули подвійного аргументу
Тут мова піде про формулах тригонометрії, що дозволяють виразити Ці формули зазвичай називають формулами подвійного аргументу. Назва, можливо, не дуже вдало, як, втім, і такі назви, як "формули приведення», «синус суми», «косинус різниці» і т.д. але це не суть важливо: головне, що є якийсь словесний символ , що дозволяє присвяченим зрозуміти, про що йде мова. Розглянемо вираз sin2х, представивши при цьому 2х у вигляді х + х. Це дозволить застосувати до вираження sin (х + х) формулу «синус суми» (див. § 21). Маємо:
Розглянемо вираз соs2х, представивши при цьому 2х у вигляді х + х. Це дозволить застосувати до вираження соs (х + х) формулу «косинус суми» (див. § 21). маємо:
Розглянемо вираз tg 2х, представивши при цьому 2х у вигляді х + х. Це дозволить застосувати до вираження tg (х + х) формулу «тангенс суми» (див. § 23). маємо:
Формули «синус подвійного аргументу» і «косинус подвійного аргументу» справедливі для будь-яких значень аргументу (ніяких обмежень немає), тоді як формула «тангенс подвійного аргументу» справедлива лише для тих значень аргументу х, для яких визначені tg х і tg 2 х, а також різниться від нуля знаменник дробу, тобто Зрозуміло, формули подвійного аргументу можна застосовувати і в тих випадках, коли місце аргументу х займає більш складне вираз. Так, справедливі наступні співвідношення:
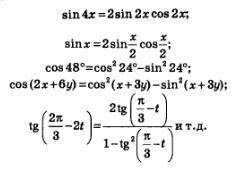
Приклад 1. Довести тотожності:
Рішення: а) Скористаємося тим, що 1 = sin 2 х + соз 2 х, і формулою синуса подвійного аргументу. отримаємо:
Приклад 2. Скоротити дріб Рішення. В чисельнику дробу скористаємося доведеним в прикладі 1 а тотожністю, а в знаменнику - формулою косинуса подвійного аргументу. отримаємо:
Приклад3. Обчислити: Рішення: а) Заданий вираз являє собою праву частину формули косинуса подвійного аргументу. Помітивши це, отримаємо
б) Заданий вираз являє собою праву частину формули синуса подвійного аргументу, але тільки не вистачає множника 2. Ввівши його, отримаємо:
в) Цей приклад значно складніше, але зате він гарніше попередніх: тут потрібно здогадатися помножити і розділити заданий вираз на 4соs18 °. Що це дасть? дивіться:
Як бачите, ми двічі скористалися формулою синуса подвійного аргументу. Щоб довести обчислення до кінця, зауважимо, що 72 ° = 90 ° -18 °. Значить, sin 72 0 = sin (90 ° -18 0) = соs18 0. Таким чином,
Приклад 4. Довести тотожність Рішення. Перетворимо ліву частину доказуваного тотожності:
Помноживши і чисельник, і знаменник останньої дробу на 2 ( «підганяємо» знаменник під формулу синуса подвійного аргументу), отримаємо:
Отже, що і було потрібно доказать.Замечаніе. Ще раз звертаємо вашу увагу на те, що тотожність доведено лише для допустимих значенні х, конкретніше для для значень х, при яких наявні знаменники відмінні від нуля.Прімер 5. Знаючи, що
Рішення: а) Скористаємося формулою sin 2 х + соз 2 х = 1. Маємо:
б) Для обчислення sin2х скористаємося формулою sin 2х = 2 sin хсоз x. Значення ство х дано в умові, а значення sin х знайдемо наступним чином. По-перше, ми вже знаємо, що По-друге, за умовою аргумент х належить четвертої чверті, а в ній синус негативний. Це означає, що з двох значенні
в) tg2х обчислимо, скориставшись визначенням тангенса:
г) Для обчислення спочатку скористаємося формулою приведення: Застосуємо до вираження соз4x формулу косинуса подвійного аргументу: соз4х = ство 2 2х - sin 2 2х. Скористаємося тим, що значення ство 2х і sin 2xуже знайдені нами:
Приклад 6. Розв'язати рівняння sin4х-соз2х = 0. Рішення. Якщо в лівій частині рівняння застосувати до вираження sin4x формулу синуса подвійного аргументу, то вдасться розкласти ліву частину на множники. Маємо послідовно: