Визначення. Нехай на площині задана пряма а і дві точки А і В. Ці точки називаються симетричними, якщо:
2) пряма а ділить відрізок навпіл (рис. 9).
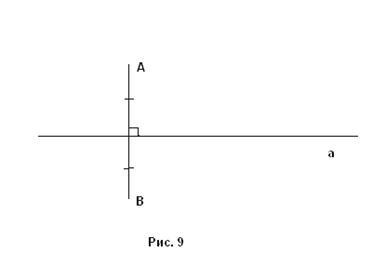
Пряма а при цьому називається віссю симетрії.
Визначення. Відображення площині в себе називається симетрією відносно осі а чи осьової симетрією, якщо кожній точці А площини ставиться у відповідність симетрична їй точка А1 щодо осі а.
Властивості осьової симетрії:
1). При осьової симетрії пряма переходить в пряму;
2). При осьової симетрії відрізок переходить в рівний йому відрізок;
3). При осьової симетрії кут переходить в рівний йому кут;
4). Осьова симетрія є рухом.
Розглянемо приклади застосування симетрії.
ПРИКЛАД 6 Дана пряма k і дві точки А і В, що не лежать на цій прямій. На k знайти таку точку Х, щоб сума АХ + ХВ була мінімальною.
Аналіз. Припустимо, що задача вирішена. Якщо точки А і В розташовані по різні боки від К, то очевидно, що Х - це точка перетину відрізка АВ і прямий k. Якщо ж точки А і В за одну сторону від k, то відобразивши У симетрично щодо k, отримаємо точку В1 таку, що ХВ = ХВ1 і значить точка Х повинна лежати на відрізку АВ1 (рис. 10).
Побудова. Якщо точки А і В по різні боки від k, то проведемо відрізок АВ і його перетин з k є шукана точка Х.
Якщо А і В за одну сторону від k, то відобразивши У симетрично щодо k, отримаємо точку В1. Провівши відрізок АВ, отримаємо шукану точку Х.
Доведення. У першому випадку доказ очевидно. У другому випадку, коли А і В за одну сторону від k: нехай Y - будь-яка інша точка прямої k, відмінна від Х. Тоді з властивостей симетрії отримуємо, що BY = B1 Y, а з нерівності трикутника маємо AY + YB = = АY + YB1> AB = AX + XB1 (рис.10).
Дослідження. Завдання має рішення завжди і причому одне.
ПРИКЛАД 7.Построіть чотирикутник АВСД, якщо задані відрізки, які є його сторонами АВ = a, ВС = b, СД = с, ТАК = d і відомо, що діагональ АС ділить кут А навпіл (рис. 11).
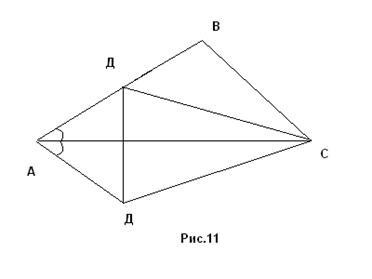
Аналіз. Припустимо задача вирішена і чотирикутник АВСД - шуканий. Тоді з двох сторін АВ і АТ одна більше. Нехай для визначеності а> d. Відобразивши симетрично точку Д відносно прямої АС отримаємо на стороні АВ точку Д1. У трикутнику ВСД1 відомі всі його сторони: ВС = b, СД = c, Д1 В = a - d. Значить трикутник Д1 ВС будується, а потім будується і весь чотирикутник.
Побудова. Будуємо трикутник Д1 ВС за трьома сторонами ВС = b, СД = с, Д1 В = а - d. Потім сторону ВД1 продовжуємо за точку Д1 і від В відкладаємо відрізок АВ = а, одержуємо точку А. Побудуємо точку Д, симетричну точці Д1 щодо АС. З'єднаємо точки А і Д, Д і С. Чотирикутник АВСD - шуканий.
Доведення. Очевидно з побудови.
Аналіз. Побудова можливо, якщо можливо побудувати трикутник Д1 ВС, тобто виконуються нерівності трикутника b <с + а + d, с <в + а – d, а – d <в + с. В этом случае задача имеет одно решение.