Не пам'ятаю, коли я вперше дізнався про топологію, але мене ця наука відразу зацікавила. Чайник перетворюється в бублик, сфера вивертається навиворіт. Багато хто чув про це. Але у тих, хто хоче заглибитися в цю тему на більш серйозному рівні, часто виникають труднощі. Особливо це відноситься до освоєння початкових понять, які за своєю суттю дуже абстрактні. Більш того, багато джерел, як ніби спеціально прагнуть заплутати читача. Скажімо російська вікі дає вельми туманне формулювання того, чим займається топологія. Там говориться, що це наука, яка вивчає топологічні простори. У статті про топологічні простори читач може дізнатися, що топологічні простори - це простору забезпечені топологією. Такі пояснення в стилі лемовскіх сепулек не надто прояснюють суть предмета. Я спробую далі викласти основні базові поняття в більш зрозумілій формі. У моїй замітка не буде перетворюються чайників і бубликів, але будуть зроблені перші кроки, які дозволять врешті-решт навчитися цієї магії.
Втім, так як я не математик, а стовідсотковий гуманітарій, то цілком можливо, що написане нижче - брехня! Ну, або принаймні частина.
Почнемо з короткого повторення теорії множин. Думаю, більшість читачів добре з нею знайомі, але тим не менше нагадаю основи.
Отже, вважається, що визначення у безлічі немає і, що ми інтуїтивно розуміємо, що це таке. Кантор говорив так: «Під« безліччю »ми розуміємо з'єднання в якесь ціле M певних добре помітних предметів m нашого споглядання або нашого мислення (які будуть називатися« елементами »безлічі M)». Звичайно, це просто алегоричне опис, а не математичне визначення.
Теорія множин відома (прошу вибачити за каламбур) безліччю дивовижних парадоксів. Наприклад. З нею також пов'язаний криза математики на початку XX-го століття.
Безлічі бувають кінцевими.

Бувають нескінченними. Наприклад, безліч цілих чисел, яке позначається буквою ℤ (або просто Z, якщо у вас на клавіатурі немає фігурних букв).

Нарешті, є порожня множина. Воно рівно одне у всьому Всесвіті. Є просте доказ цього факту, але я не буду його тут наводити.

Якщо безліч нескінченно, воно буває рахунковим. Рахункові - ті безлічі, елементи яких можна перенумерувати натуральними числами. Саме безліч натуральних чисел, як ви здогадалися, теж лічильно. А ось як можна пронумерувати цілі числа.
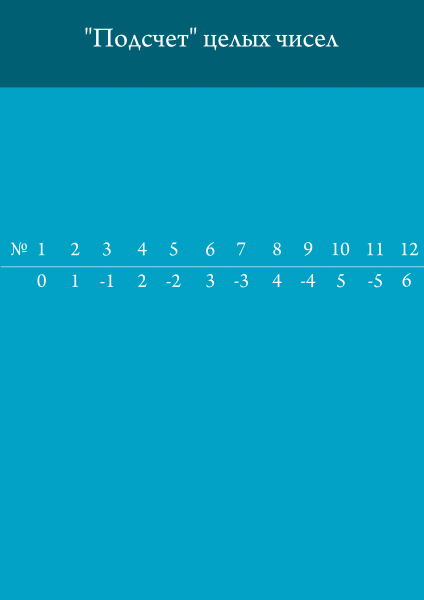
З раціональними числами складніше, але і вони піддаються нумерації. Цей спосіб називається діагональним процесом і виглядає, як на картинці внизу.
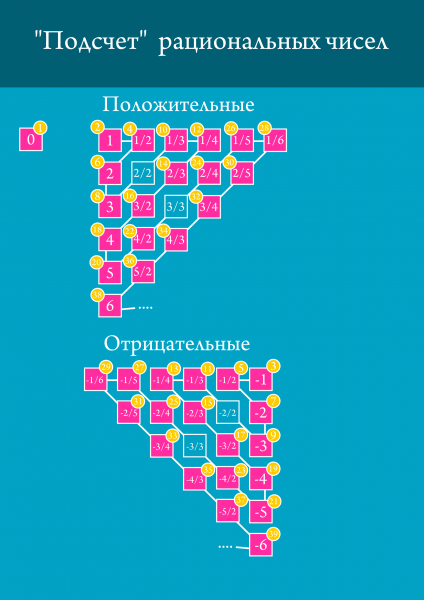
Ми зигзагом рухаємося по раціональним числам, починаючи з 1. При цьому кожному числу, яке у нас виходить, присвоюємо парний номер. Негативні раціональні числа вважаються тим же способом, тільки номери непарні, починаючи з 3. Нуль традиційно отримує перший номер. Таким чином видно, що всі раціональні числа можна пронумерувати. Всі числа начебто 4,87592692976340586068 або +1,00000000000001, або -9092, або навіть 42 отримують свій номер в цій таблиці. Проте, сюди потрапляють не всі числа. Наприклад, √2 не отримає номера. Колись це дуже засмутило греків. Кажуть, того хлопця, який відкрив ірраціональні числа, втопили.
Узагальненням поняття розміру для множин є потужність. Потужність кінцевих множин дорівнює числу їх елементів. Потужність нескінченних множин позначається єврейської буквою алеф з індексом. Найменша нескінченна потужність-це потужність ℵ0. Вона дорівнює потужності рахункових множин. Як бачимо, таким чином, натуральних чисел, так само багато, як і цілих або раціональних. Дивно, але факт. Наступна - потужність континууму. Вона позначається ℵ1. Це потужність безлічі дійсних чисел ℝ, наприклад. Існує гіпотеза про те, що потужність континууму і потужність алеф-один - одне і те ж. Тобто що немає ніякої проміжної потужності меду рахунковими множинами і континуумом.
Над множинами можна проводити різні операції і отримувати нові множини.
1. Множини можна об'єднувати.

2. Безліч можна «вичитати». Ця операція називається доповненням.

3. Можна шукати перетин множин.
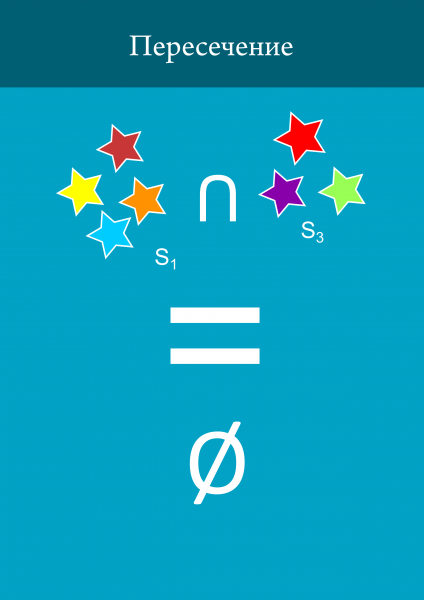
Власне це все про множини, що потрібно знати для цілей цієї замітки. Тепер ми можемо приступити до самої топології.
Топологія - це наука, яка вивчає безлічі з певною структурою. Ця структура також називається топологією.
Нехай у нас є деякий непорожня множина S.
Нехай же у цього безлічі буде деяка структура, яка описується за допомогою безлічі, яке ми назвемо Т. Т являє собою безліч підмножин множини S таке, що:
1. Саме S і ∅ належать T.
2. Будь-яке об'єднання довільних сімейств елементів T належить T.
3. Перетин довільного кінцевого сімейства елементів T належить T.
Якщо ці три пункти виконуються, то наша структура є топологією T на безлічі S. Елементи безлічі T називаються відкритими множинами на S в топології T. Доповненням до відкритих множин є замкнуті безлічі. Важливо відзначити, що якщо безліч відкрито, це ще не означає, що воно не замкнуто і навпаки. Крім того в даному безлічі щодо деякої топології можуть бути підмножини, які не є ні відкритими, ні замкнутими.
Наведемо приклад. Нехай у нас є безліч, що складається з трьох кольорових трикутників.

Найпростіша топологія на ньому сидів, зветься антідіскретной топологією. Ось вона.

Цю топологію, також називають топологією злиплих точок. Вона складається з самого безлічі і з порожньої множини. Це дійсно задовольняє аксіомам топології.
На одному безлічі можна задати кілька топологій. Ось ще одна дуже примітивна топологія, яка буває. Вона називається дискретною. Це топологія, яка складається з усіх підмножин даної множини.

А ось ще топологія. Вона задана на безлічі з 7 різнокольорових зірок S, які я позначив буквами. Переконайтеся, що це топологія. Я в цьому не впевнений, раптом я пропустив, якесь об'єднання чи перетин. На цій картинці повинне бути саме безліч S, порожня множина, перетину і об'єднання всіх інших елементів топології також повинні бути на зображенні.

Пара з топології і безлічі на якому вона задана називається топологічним простором.
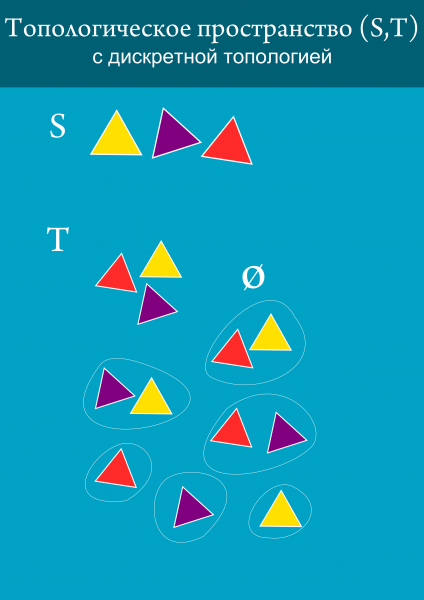
Якщо в безлічі багато точок (не кажучи вже про те, що їх може бути нескінченно багато), то перелічити всі відкриті множини може бути проблематично. Наприклад, для дискретної топології на множині з трьох елементів, треба скласти список з 8 множин. А для 4-елементного безлічі дискретна топологія налічуватиме вже 16, для 5 - 32, для 6 -64 і так далі. Для того, щоб не перераховувати всі відкриті множини використовується як би скорочений запис - виписуються ті елементи, об'єднання яких можуть дати, всі відкриті множини. Це називається базою топології. Наприклад, для дискретної топології простору з трьох трикутників - це будуть три трикутника взяті окремо, тому, що об'єднуючи їх, можна отримати всі інші відкриті множини в даній топології. Кажуть, що база генерує топологію. Безлічі, елементи якого генерують базу, називають предбазой.
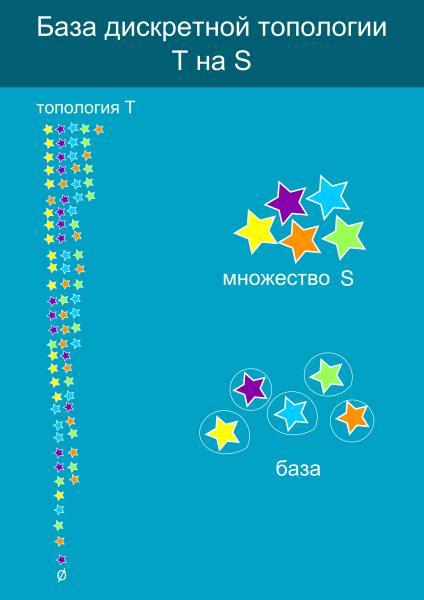
Нижче приклад бази для дискретної топології на множині з п'яти зірок. Як бачите, в даному випадку база складається всього з п'яти елементів, в той час як в топології цілих 32 підмножини. Погодьтеся, використовувати базу для опису топології - набагато зручніше.
Для чого потрібні відкриті множини? В якомусь сенсі вони дають уявлення про «близькості» між точками і про відмінність між ними. Якщо точки належать двом різним відкритим множинам або якщо одна точка знаходиться у відкритому безлічі, в якому не знаходиться друга, то вони топологічно розрізняються. У антідіскретной топології всі крапки в цьому сенсі невиразні, вони як би злиплися. Навпаки, в дискретної топології всі крапки мають відмінність.

Зв'язок між відкритим безліччю і октестностью можна сформулювати так. Відкрите безліч - таку силу-силенну, кожен елемент якого має деяку околицю. Або навпаки можна сказати, що безліч відкрито, якщо воно є околицею будь-якої своєї точки.
Все це базові поняття топології. Звідси ще не ясно як вивертати сфери навиворіт. Можливо в майбутньому, я зможу дістатися і до такого роду тем (якщо сам розберуся).