Короткий опис документа:
Наступний приклад розглядає додаток поняття похідною під час вирішення геометричних задач. Для цього спочатку розкривається поняття дотичній. На координатної площині зображується графік функції, на якому зазначаються дві точки M і S. Через відмічені точки проводиться пряма. Демонструється, як при наближенні точки S до точки М становище з'єднує точки прямої наближається до положення дотичної в точці М. Тобто дотична є граничне положення січної, що з'єднує дві точки графіка при зближенні точок. Після введення поняття дотичній розглядається дотична до графіка функції y = f (x) в точці М (а, f (a)). Необхідно знайти кутовий коефіцієнт дотичної. Для цього на деякій відстані від М відзначається точка N (а + δх, f (a + δх)). Кутовий коефіцієнт прямої представляє тангенс кута, під яким лежить пряма, яка містить гіпотенузу трикутника, утвореного збільшенням аргументу δх і збільшенням функції δу. Відповідно, кутовий коефіцієнт січної знаходиться за формулою kсек. = Δу / δх. При наближенні точок δх → 0. Очевидно, що коефіцієнт дотичної при зближенні точок визначається граничним становищем січної при δх → 0, kкас. = Lim kсек. або kкас. = lim δу / δх.
Висновки з особливостей математичної моделі рішення обох задач оформляються у вигляді визначення похідної функції, перебування якої фігурує в задачах. Відзначається, що для функції y = f (x), визначеної в точці х і її околиці, межа δу / δх при δх → 0 називається похідною y = f (x) в цій точці. Вводиться позначення похідної f '(x). Для засвоєння матеріалу розглядається похідна лінійної функції - зазначається, що так як знайдений раніше для функції y = kx + m межа lim δу / δх = k при δх → 0, то y '= (kx + m)' = k. Також, знайдений межа функції y = x 3. рівний lim δу / δх = 3х 2 при δх → 0 означає, що похідна y '= (x 3)' = 3х 2.
Розкривається фізичний і геометричний зміст похідної. Відзначено, що у фізичному сенсі для закону прямолінійного руху s (t) похідна означає миттєву швидкість v = s '(t). У геометричному сенсі для дотичній. проведеної в точці х = а до графіка функції y = f (x) похідна f '(а) - кутовий коефіцієнт дотичної.
Розглядаючи зміст похідної і формулу для її знаходження lim δу / δх = f '(х) при δх → 0, відзначається майже пряма пропорційність приросту функції від збільшення аргументу з коефіцієнтом, що представляє собою похідну δу≈f' (х) · δх. Таким чином, для похідної функції y = x 3 правильне співвідношення δу≈3х 2 · δх.
Дається алгоритм знаходження похідної функції, в якому потрібно:
- У точці х знайти f (x);
- При переході в точку х + δх знайти f (х + δх);
- Знайти приріст функції f (х + δх) - f (x);
- Скласти ставлення δу / δх;
- Знайти lim δу / δх при δх → 0, тобто f '(х).
Згідно з цим алгоритмом, демонструються приклади визначення похідної функцій f (x) = С, де (С) '= 0; f (x) = 1 / х, де (1 / х) '= - 1 / х 2.
Розкривається поняття диференціювання функції, тобто знаходження її похідної. Відзначається, що функція є диференційованою в точці, якщо вона має в ній похідну, а також дифференцируемость функції в точці означає безперервність функції в ній, при цьому зворотне твердження не так. Підтверджує прикладом цього твердження є знаходження похідної в точці х = 0 функції у = | x |. Відзначається, що незважаючи на безперервність функції в цій точці, дотичної до графіка в ній не може бути. А значить, і немає в цій точці похідної. Даний висновок відображений на екрані окремо і рекомендований для запам'ятовування. Прикладом твердження служить функція y = f (x), яка на х<0 равна -√-х, а на промежутке x>= 0 дорівнює √х. На малюнку побудований графік функції, на якому добре видно безперервність функції. Однак в точці х = 0 дотичну до графіка побудувати не можна, тому в цій точці немає похідною. Нагадується, що якщо в деякій точці графіка функції дотичну побудувати не можна, або вона перпендикулярна осі абсцис, функція недіфференціруемого. В даному прикладі функція недіфференціруемого. На довільному графіку функції в останньому прикладі розглядається її дифференцируемость в трьох точках.

Розглянемо дві різні завдання, фізичну і геометричну, які як приведуть до виникнення нової математичної моделі.
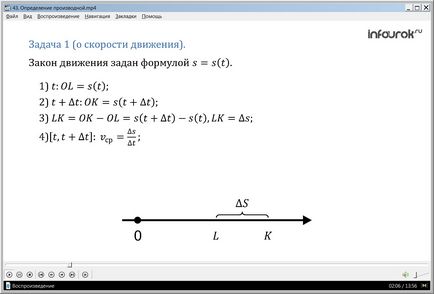
Завдання 1 (про швидкість руху). По прямій, на якій задані початок відліку, одиниця виміру (метр) і напрямок, рухається деякий тіло (матеріальна точка). Закон руху заданий формулою s = s (t) (ес рівне ес від ТЕ), де t - час (в секундах), s (t) - становище тіла на прямий (координата рухається матеріальної точки) в момент часу t по відношенню до початку відліку (в метрах). Знайти швидкість руху тіла в момент часу t (в м / с).
Рішення. Припустимо, що в момент часу t тіло знаходилося в точці
L (рис. 1), пройшовши шлях від початку руху ОL = s (t). Дамо аргументу t
приріст δt (дельта те) і розглянемо момент часу t + δt. Координата матеріальної точки стала іншою, тіло в цей момент буде знаходитися в точці K: OK = s (t + t) (про ка одно ес від ТЕ плюс дельта те).
Значить, за t секунд тіло перемістилося з точки L в точку K, тобто пройшло шлях LK. Маємо: LK = ОK-ОL = s (t + t) -s (t). Отриману різницю ми назвали збільшенням функції: s (t + t) -s (t) = s. Отже, LK = s (метрів).
Шлях s (метрів) тіло пройшло за t секунд. Неважко знайти середню швидкість руху тіла за проміжок часу [t, t + t]: vср. = (М / с) (середня швидкість дорівнює відношенню дельта ес до дельта те).
А що таке швидкість v (t) в момент часу t (її називають іноді миттєвою швидкістю). Можна сказати так: це середня швидкість руху за проміжок часу [t, t + t] за умови, що t вибирається все менше і менше; іншими словами, за умови, що t0. Це означає що
v (t) = (ве від ТЕ одно межі середньої швидкості) і
Підводячи підсумок вирішення завдання 1, отримуємо:
Для вирішення наступного завдання нам потрібно з'ясувати, що слід розуміти під дотичної до кривої.
Дана крива L (рис. 2), на ній обрана точка М. Візьмемо ще одну точку на кривій, причому досить близьку до М, - точку S.
Проведемо січну МS. Далі будемо наближати точку S по кривій L до
точці М. Січна МS буде змінювати своє положення, вона як би повертається навколо точки М. Часто буває так, що можна виявити в цьому процесі пряму, що представляє собою якесь граничне положення січної; цю пряму - граничне положення січної - називають
дотичної до кривої L в точці М.
Завдання 2 (про дотичної до графіка функції). Дан графік функції y = f (x). На ньому обрана точка М (а; f (a)) (ем з координатами а і еф від а). в цій точці до графіка функції проведена дотична (ми припускаємо, що вона існує).
Знайти кутовий коефіцієнт дотичної.
Рішення. Дамо аргументу приріст х і розглянемо на графіку (рис. 3) точку N з абсцисою а + х. Ордината точки N дорівнює f (a + x). Кутовий коефіцієнт січної МN. тобто тангенс кута між січною і віссю х. обчислюється за формулою (ка січною дорівнює дельта ігрек, поділене на дельта ікс).
Якщо ми тепер спрямуємо х до нуля, то точка N почне наближатися по кривій до точки М. Дотичну ми характеризували
як граничне положення січної при цьому наближенні. Значить, природно вважати, що кутовий коефіцієнт дотичної kкac буде обчислюватися по формулі (ка дотичній одно межі ка січною).
Використовуючи наведену вище формулу для kсек. отримуємо: (ка дотичній одно межа дельта ігрек, поділене на дельта ікс, при прагненні дельта ікс до нуля).
Підведемо підсумки. У процесі вирішення двох задач ми прийшли до однієї і тієї ж математичної моделі - межі відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
Розглянемо, що з себе представляє границя відношення приросту функції до приросту аргументу.
2. Визначення похідної
Визначення 1. Нехай функція у = f (x) визначена в конкретній точці х і в деякій її околиці. Дамо аргументу х приріст х, таке, щоб не вийти з зазначеної околиці. Знайдемо відповідне прирощення функції δу і складемо відношення. Якщо існує межа цього відношення за умови х0, то вказану межу називають похідною функції у = f (х) в точці х і позначають f '(x) (еф штрих від ікс).
Отже, (межа дельта ігрек, поділене на дельта ікс, дорівнює еф штрих від ікс).
Для позначення похідної часто використовують символ у '. (Ігрек штрих)
Відзначимо, що у '= f' (x) (ігрек штрих дорівнює еф штрих від ікс) - це нова функція, але, пов'язана з функцією y = f (x), певна в усіх таких точках х, в яких існує вказаний вище межа . Цю функцію називають так: похідна функції у = f (x).
У прикладі для лінійної функції y = kx + m справедливо рівність.
Це означає, що y '= k або, докладніше,
Ми довели, що для функції у = х 3 справедливо рівність
Це означає, що у '= 3х 2 або, докладніше, (x 3)' = 3х 2. (Ікс в кубі штрих одно три ікс в другому ступені)
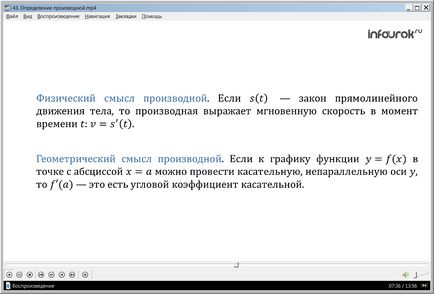
Похідна з фізичної та геометричної точок зору.
Фізичний (механічний) зміст похідної полягає в наступному. Якщо s (t) - закон прямолінійного руху тіла, то похідна виражає миттєву швидкість в момент часу t:
v = s'(t) (ве одно ес штрих від ТЕ).
Геометричний зміст похідної полягає в наступному. Якщо до графіка функції y = f (x) в точці з абсцисою х = а можна провести дотичну, непаралельність осі у, то f '(a) -це є кутовий коефіцієнт дотичної.
Нехай функція у = f (x) має похідну в конкретній точці х: (границя відношення приросту функції до приросту аргументу дорівнює похідної функції).
Отримуємо: в досить малій околиці точки х виконується наближена рівність: (відношення приросту функції до приросту аргументу приблизно однаково похідною функції) або
y f '(x) · х. (Приросту функції наближено одно похідної функції, помноженої на приріст аргументу).
Приріст функції «майже пропорційно» приросту аргументу, причому коефіцієнтом пропорційності є значення похідної (в заданій точці х). Наприклад, для функції у = х 3 справедливо наближене рівність y 3х 2 · х
Сформулюємо алгоритм відшукання похідної.
АЛГОРИТМ відшукання ПОХІДНОЇ (для функції у = f (x))
1. Зафіксувати значення х, знайти f (x).
2. Дати аргументу х приріст х, перейти в нову точку
х + х, знайти f (x + x).
3. Знайти приріст функції: y = f (x + x) -f (x).
4. Скласти відношення.
5. Обчислити межа.
Ця межа і є f '(x).
Приклад 1. Знайти похідну постійної функції у = С.
Рішення. Скористаємося алгоритмом відшукання похідної.
1) Для фіксованого значення х маємо: f (х) = С.
2) В точці х + х маємо: f (x + х) = С.
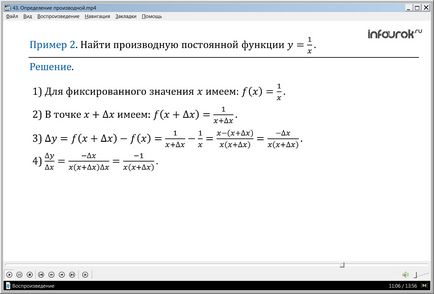
Приклад 2. Знайти похідну функції у =.
Рішення. Скористаємося алгоритмом відшукання похідної.
Якщо функція y = f (x) має похідну в точці х, то її називають диференційованою в точці х. Знаходження похідної функції y = f (x) називається диференціюванням функції y = f (x).
Якщо функція диференційовна в точці х, то вона і неперервна в цій точці.
Зворотне ж твердження не так.
Наведемо приклади: функція y = | х | неперервна скрізь, і в точці х = 0 (рис. 4), але дотичної до графіка функції в «точці стику» (0; 0) не існує.
Якщо в деякій точці до графіка функції можна провести дотичну, то в цій точці не існує похідною.
Приклад. На рис. 5 зображено графік кусочной функції y = f (x), де
Функція неперервна на всій числовій прямій, в тому числі в точці х = 0. І дотична до графіка функції існує в будь-якій точці, в тому числі в точці х = 0. Але в точці х = 0 дотична збігається з віссю у, тобто перпендикулярна осі абсцис, її рівняння має вигляд х = 0.Такая пряма не має кутового коефіцієнта, тому, не існує і f '(0).
Щоб за графіком зробити висновок про дифференцируемости функції, необхідно перевірити, чи можна в деякій точці провести дотичну до графіка функції, не перпендикулярну осі абсцис. Якщо можна, тоді в цій точці функція диференційована. Якщо в деякій точці дотична до графіка функції не існує або вона перпендикулярна осі абсцис, то в цій точці функція недіфференціруемого. Так, за графіком функції, зображеному на рис. 6, можна зробити висновок: функція неперервна всюди, крім точки х = а; функція диференційована всюди, крім точок х = а, х = b - тут дотична не існує, х = з-тут дотична паралельна осі у.