Короткий опис документа:
ТЕКСТОВА Розшифровка УРОКУ:
Ми продовжуємо знайомство з рухом.
На минулому занятті ви дізналися про ще одному виді руху - осьової симетрії.
Нагадаю, що осьова симетрія з віссю а - це відображення простору на себе, при якому будь-яка точка К переходить в симетричну їй точку К1 щодо осі а.
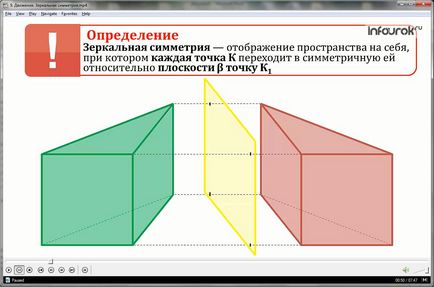
Відображення простору на себе, при якому кожна точка К переходить в симетричну їй відносно площини β точку К1 називається дзеркальною симетрією (симетрією відносно площини β).
1. Введемо декартову (прямокутну) систему координат Оxyz так, щоб площина Оxy збіглася з площиною симетрії.
2. Знайдемо зв'язок між точками М (x; y; z) і M1 (x1; y1; z1), які симетричні відносно площини Оxy. Якщо точка М не належить даній площині, то площину Оxy:
а) проходить через середину відрізка МM1;
б) перпендикулярна відрізку ММ1.
З першої умови за формулами для координат середини відрізка маємо:
z + z1 = 0, звідки z = -z1
З другої умови випливає, що відрізок МM1 паралельний осі аплікат Оz. таким чином, x = x1; y = y1.
Дані формули вірні і в тому випадку, якщо точка М лежить в площині Оxy.
3. Розглянемо будь-які дві точки: А - з координатами (x1; y1; z1) і В - з координатами (x2; y2; z2) і доведемо, що відстань між точками А1 і В1, які їм симетричні, так само АВ.
Точки А1 і В1 мають координати
А1 (x1; y1; -z1) і В1 (x2; y2; -z2).
За формулою відстаней між двома точками, знайдемо:
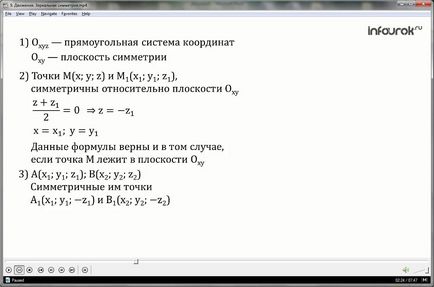
Очевидно, що довжина відрізка АВ дорівнює довжині відрізка A1B1, тобто відстань між точками збережено.
Таким чином, ми довели, що дзеркальна симетрія є рухом.
Розберемо кілька завдань, застосовуючи отримані знання.
Довести, що прямі а і а1 лежать в одній площині, якщо при дзеркальній симетрії пряма а відображається в пряму а1.
1. Введемо площину симетрії Оxy.
Розглянемо два випадки:
- пряма а паралельна площині Оxy.
- пряма а не паралельна площині Оxy.
У разі паралельності прямої а і площини Оxy маємо: точки М і L, N і K симетричні (належать симетричним прямим), тоді MA = AL, NB = BK.
Крім того, всі ці відрізки рівні між собою: MA = AL = NB = BK, оскільки площина Оxy - площину симетрії.
Прямі МL, NK - перпендикулярні площині Оxy, значить МL паралельна NK (дві прямі, перпендикулярні площині, паралельні між собою).
Таким чином, ми отримали, що чотирикутник MLKN - прямокутник.
Тому прямі LK і MN паралельні як протилежні сторони прямокутника MLKN. А значить, і прямі а і а1, на яких лежать паралельні прямі LK і MN, будуть паралельними, а значить, і лежать в одній площині.
Що й потрібно було довести.

2.В разі, якщо пряма а не паралельна площині Оxy, пряма а перетинає дану площину в точці Р.
При симетрії точка Р переходить в себе, так як лежить в площині симетрії Оxy.
Таким чином, точка Р належить і прямий а1.
Ми отримали, що прямі а і а1 мають спільну точку, отже, вони лежать в одній площині.
Що й потрібно було довести.
Отже, ми довели, що прямі а і а1 завжди лежать в одній площині, якщо при дзеркальній симетрії пряма а відображається в пряму а1.
При дзеркальної симетрії відносно площини α площину β відображається на площину β1. Довести, що якщо площину β паралельна площині α, то площину β1 також паралельна площині α.
1.Виберіте три точки А, В, С в площині β, що не лежать на одній прямій.
2.Дополнітельное побудова: проведемо відрізки АА2, ВВ2, СС2 перпендикулярно площині α.
Продовжимо ці відрізки за точки А1, В1, С1 так, що А2А1 = АА2, В2В1 = ВВ2, С2С1 = СС2.
Ми отримали, що чотирикутник АА1В1В - прямокутник, так як Аа1 = ВВ1 і АА1║ВВ1 (в силу симетричності площин β і β1).
3.Так чином, А1В1║АВ, ВВ1 = СС 1 і ВВ1║СС1, значить ВВ1С1С - прямокутник.
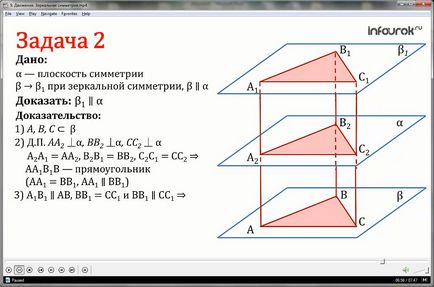
4.Плоскость β проходить через точки А1, В1, С1 і ця площина єдина.
5. Відомо, що якщо пересічні прямі (ВА і ВС) одній площині (β) паралельні двом пересічним прямим (В1А1 і В1С1) іншій площині (β1), то ці площини паралельні.
Отже, ми довели, що площині β і β1 паралельні.