«Сплайни. Фінітні функції. Основні поняття, призначення. У сплайни Шенберга »
Функції, подібні до тих, що зараз називають сплайнами були відомі математикам давно, починаючи як мінімум з Ейлера, але їх інтенсивне вивчення почалося, фактично, тільки в середині XX століття. У 1946 році Ісаак Шенберг вперше вжив цей термін як позначення класу поліноміальних сплайнів. До 1960 років сплайни були в основному інструментом теоретичних досліджень, вони часто з'являлися в якості рішень різних екстремальних і варіаційних задач, особливо в теорії наближень.
Після 1960 року з розвитком обчислювальної техніки почалося використання сплайнів в комп'ютерній графіці і моделюванні, що триває донині.
Під сплайном (від англ. Spline - планка, рейка) зазвичай розуміють кусочно-задану функцію, збігається з функціями більш простої природи на кожному елементі розбиття своєї області визначення.
Класичний сплайн однієї змінної будується так: область визначення розбивається на кінцеве число відрізків, на кожному з яких сплайн збігається з деяким алгебраїчним поліномом. Максимальний ступінь з використаних поліномів називається ступенем сплайна. Різниця між ступенем сплайна і вийшла гладкістю називається дефектом сплайна. Наприклад, безперервна ламана є сплайн ступеня 1 і дефекту 1.
Сплайни мають численні застосування як в математичній теорії, так і в різноманітних обчислювальних додатках. Зокрема, сплайни двох змінних інтенсивно використовуються для завдання поверхонь в різних системах комп'ютерного моделювання.
1.1 Криві Безьє
Криві Безьє або криві Бернштейна-Безьє були розроблені в 60-х роках XX століття незалежно один від одного П'єром Безьє і Полем де Кастельжо.
Вперше криві були представлені широкій публіці в 1962 році французьким інженером П'єром Безьє, який, розробивши їх незалежно від де Кастельжо, використовував їх для комп'ютерного проектування автомобільних кузовів. Криві були названі ім'ям Безьє, а ім'ям де Кастельжо названий розроблений ним рекурсивний спосіб визначення кривих (алгоритм де Кастельжо).
Згодом це відкриття стало одним з найважливіших інструментів систем автоматизованого проектування і програм комп'ютерної графіки.
Крива Безьє - параметрична крива, що задається виразом:
- функція компонент векторів опорних вершин, а
, апроксимація її першої похідної
.
Наявність такої центральної теореми, а також ще ряду доведених стренгами-Фіксом теорем, зокрема про існування функцій, які відповідають умовам (2.7), дає алгоритм для побудови базисних фінітних функцій, що володіють необхідними Апроксимаційні властивостями.
3. B-сплайни Шенберга
У обчислювальної математики B-сплайном називають сплайн-функцію, що має найменший носій для заданого ступеня, порядку гладкості і розбиття області визначення. Фундаментальна теорема встановлює, що будь-яка сплайн-функція для заданого ступеня, гладкості та області визначення може бути представлена як лінійна комбінація B-сплайнів тій же мірі і гладкості на тій же області визначення. [1] Термін B-сплайн був введений І. Шенберга і є скороченням від словосполучення «базисний сплайн». [2] B-сплайни можуть бути обчислені за допомогою алгоритму де Бора, що володіє стійкістю.
У системах автоматизованого проектування та комп'ютерної графіки термін B-сплайн часто описує сплайн-криву, яка задана сплайн-функціями, вираженими лінійними комбінаціями B-сплайнів.
Коли вузли рівновіддалені один від одного, кажуть, що B-сплайн є однорідним, в іншому випадку його називають неоднорідним.
Коли кількість вузлів збігається зі ступенем сплайна, B-сплайн вироджується в криву Безьє. Форма базисної функції визначається розташуванням вузлів. Масштабування або паралельний перенос базисного вектора не впливає на базисну функцію.
Сплайн міститься в опуклій оболонці його опорних точок.
Базисний сплайн ступеня n:
.
не звертається до нуль тільки на проміжку [ti, ti + n + 1], тобто:
Іншими словами, зміна однієї опорної точки впливає тільки на локальне поведінка кривої, а не на глобальне, як у випадку кривих Безьє.
Базисна функція може бути отримана з полінома Бернштейна
По-сплайн і деякі найбільш часто використовувані базиси
Теорема Стренга-Фікса вказує на те, що якщо стандартну ФІНІТНОГО функцію
вибрати виходячи з умови (2.7), то ряд (2.4), побудований на основі її зрушень, буде мати гарні Апроксимаційні властивостями.
Шенберг запропонував один цікавий клас функцій, що задовольняють умові (2.7). функцію
називають В-сплайном (Шенберга) ступеня
, якщо її перетворення Фур'є має вигляд
Як бачимо, функція (6.8) задовольняє всім умовам (6.7).
Базис зі сходинок
Досить просто показати, що при
являє собою апроксимацію безперервної ламаною лінією, що має розривні похідні. Апроксимація по нормі
має другий порядок, за нормою
- перший. Ця апроксимація використовується найбільш часто при вирішенні диференціальних рівнянь другого порядку проекційним методом. Вона призводить до найбільш простим формулам для інтегралів і максимально розрідженій матриці при її обчисленні.
Крім того, у цього базису, з огляду на те, що p = 1, є одна особливість - для функції, що апроксимується
збігаються зі значеннями функції у вузлах сітки
, що дозволяє швидко знаходити початкові наближення для
.
являє собою кусково-поліномінальної кубічний сплайн, який виходить сверткой:
.
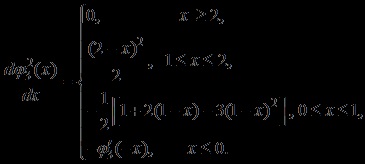
Розмір носія при
збільшився до чотирьох (
). Зауважимо, що для забезпечення безперервності другої похідної в точках
. Як уже зазначалося, апроксимація за нормою
має четвертий порядок, за нормою
5. Алберг Дж. Нільсон Е. Уолш Дж. - Теорія сплайнів та її застосування