СИНТЕЗ КОМБІНАЦІЙНИХ ПРИСТРОЇВ
Канонічні форми представлення логічних функцій.
Синтез логічного пристрою розпадається на кілька етапів. На першому етапі потрібно функцію, задану у словесній, табличній або інший формах, представити у вигляді логічного виразу з використанням деякого базису. Наступні етапи зводяться до отримання мінімальних форм функцій, що забезпечують при синтезі найменшу кількість електронного обладнання та раціональне побудова функціональної схеми пристрою. Для початкового представлення функції зазвичай використовується базис І, АБО, НЕ незалежно від того, який базис буде використовуватися для побудови логічного пристрою.
Вихідними, з міркувань зручності подальших перетворень, прийняті наступні дві канонічні форми представлення функцій: досконала діз'юнктівная нормальна форма (СДНФ) і досконала кон'юнктивна нормальна форма (СКНФ).
^ Досконала діз'юнктівная нормальна форма (СДНФ).
Диз'юнктивній нормальною формою (ДНФ) називається така форма представлення функції, при якій логічне вираження функції будується в вигляді диз'юнкції ряду членів, кожен з яких є простою кон'юнкція аргументів або їх інверсій.
Прикладом ДНФ може служити вираз
Наведемо форму представлення функцій, що не є ДНФ. Наприклад, функція
представлена не в ДНФ, так як останній член не є простою кон'юнкція аргументів.
Також не є ДНФ наступна форма представлення функції:
Якщо в кожному члені ДНФ представлені всі аргументи (або їх інверсії) функції, то така форма носить назву досконалої диз'юнктивній нормальної форми (СДНФ). Вираз (3.9) не є СДНФ, так як в ньому лише третій член містить всі аргументи функції.
Для переходу від ДНФ до СДНФ необхідно в кожен з членів, в яких представлені не всі аргументи, ввести вираз виду, де xi - відсутній в члені аргумент. Так як, така операція не може змінити значень функції. Покажемо перехід від ДНФ до СДНФ на прикладі наступного виразу:
Додавання в члени виразів виду призведе функцію до виду
На підставі (3.1)
Звідси після приведення подібних членів:
Отримана форма є СДНФ. Якщо початкова функція дана в табличній формі, то СДНФ може бути отримана безпосередньо.
Нехай дана функція в формі табл. 3.4. Для цієї функції СДНФ має вигляд
Як видно з виразу (3.10), в ньому кожен член відповідає певному набору значень аргументів, при якому функція
дорівнює 1. Кожен з наборів аргументів, при яких дорівнює 1 (3, 4, 6, 8-й стовпці наборів), звертає в одиницю відповідний член виразу (3.10), внаслідок чого і вся функція виявляється Раїна одиниці.
Можна сформулювати наступне правило записи СДНФ функції, заданої таблицею істинності.
Необхідно записати стільки членів в вигляді кон'юнкція всіх аргументів, скільки одиниць містить функція в таблиці. Кожна кон'юнкція повинна відповідати певному набору значень аргументів, звертається функцію в одиницю, і якщо в цьому наборі значення аргументу дорівнює нулю, то в кон'юнкцію входить .інверсія даного аргументу.
Слід зазначити, що будь-яка функція має єдину СДНФ.
^ Досконала кон'юнктивна нормальна форма (СКНФ).
Кон'юнктівной нормальною формою (КНФ) називається форма представлення функції у вигляді кон'юнкції ряду членів, кожен з яких є простою диз'юнкція аргументів (або їх інверсій).
Прикладом КНФ може служити наступна форма представлення функції:
Наведемо форми представлення функцій, які не є КНФ:
(Тут третій член не є простою диз'юнкція аргументів або їх інверсій);
(Ця форма також не є КНФ, так як в ній перший член групи не належить з іншими операцією кон'юнкції).
У досконалої кон'юнктивній нормальній формі (СКНФ) в кожному члені КНФ повинні бути представлені всі аргументи.
Для переходу від КНФ до СКНФ необхідно додати до кожного члена, який не містить всіх аргументів, члени виду. де хi - аргумент, не представлений в члені. Так як
, то така операція не може вплинути на значення функції.
Додавання до деякого члену утворює вираз виду. яке можна привести до виду
Справедливість цього рівності випливає з розподільного закону;
вона може бути показана також шляхом розкриття дужок в правій частині виразу:
Розглянемо перехід від КНФ до СКІФ на прикладі функції
Покажемо застосування розподільного закону прн проведенні використаних тут перетворень над одним з членів виразу
Позначимо Тоді на підставі розподільного закону
Далі позначимо і знову застосуємо розподільний закон
Підставивши сюди значення z1 і z2 отримаємо відповідні члени наведеного вище виразу при переході від КНФ до СКНФ.
Досконала КНФ функції легко будується по таблиці істинності.
Розглянемо як приклад функцію, наведену в табл. 3.4; СКНФ цієї функції має вигляд
Вираз містить стільки членів, пов'язаних операцією кон'юнкції, скільки нулів є серед значень функції f (x1, x2, x3) в таблиці істинності. Таким чином, кожному набору значень аргументів, на якому функція дорівнює нулю, відповідає певний член СКНФ, що приймає на цьому наборі значення нуль. Так як члени СКНФ пов'язані операцією кон'юнкції, при зверненні в нуль одного з членів і вся функція виявляється рівною нулю.
Таким чином, можна сформулювати наступне правило записи СКНФ функції, заданої таблицею істинності.
Слід записати стільки кон'юнктивні членів, що представляють собою диз'юнкції всіх аргументів, при скількох наборах значень аргументів функція дорівнює нулю, і якщо в наборі значення аргументу дорівнює одиниці, то в диз'юнкцію входить інверсія цього аргументу. Будь-яка функція має єдину СКНФ.
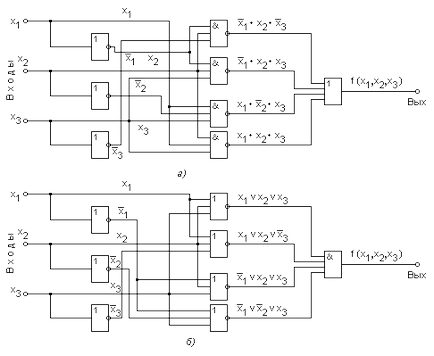
Структурна схема логічного пристрою може бути побудована безпосередньо по канонічної формі (СДНФ або СКНФ) реалізованої функції. Отримувані при цьому схеми для функцій (3.10) і (3.11) показані на рис. 3.26, а і б. Недолік такого методу побудови структурних схем, що забезпечує, в загальному, правильне функціонування пристрою, полягає в тому, що виходять схеми, як правило, виявляються невиправдано складними, вимагають використання великої кількості логічних елементів і, отже, мають низькі економічність і надійність.
У багатьох випадках вдається так спростити логічний вираз, не порушуючи функції, що відповідна структурна схема виявляється істотно простіший.
Методи такого спрощення функції, звані методами мінімізації функцій, розглядаються нижче.
Мінімізація логічних функцій методом Квайна
Метод Квайна відноситься до числа таких методів мінімізації функції алгебри логіки, які дозволяють представляти функції в ДНФ або КНФ з мінімальним числом членів і мінімальним числом букв в членах. Цей метод містить два етапи перетворення виразу функції: на першому етапі здійснюється перехід від канонічної форми (СДНФ або СКНФ) до так званою скороченою формою, на другому етапі-перехід від скороченої форми логічного виразу до мінімальної формі.
^ Перший етап (отримання скороченої форми).
Нехай задана функція f представлена в СДНФ.
Перехід до скороченій формі заснований на послідовному застосуванні двох операцій: операції склеювання і операції поглинання.
Для виконання операції склеювання виявляються в вираженні пари членів виду і. розрізняються лише тим, що один з аргументів на одному з членів представлений без інверсії, в іншому-з інверсією. Потім проводиться склеювання таких пар членів. та результатами тати склеювання w вводяться в вираз функції в якості додаткових членів. Далі проводиться операція поглинання. Вона заснована на рівності
(Член w поглинає член w? Z). При проведенні цієї операції з логічного виразу викреслюються всі члени, що поглинаються членами, які введені в результаті проведення операції склеювання.
Операції склеювання і поглинання проводяться послідовно доти, поки їх виконання виявляється можливим.
Покажемо виконання цих операцій стосовно функції, представленої в табл. 3.5.
Записуємо СДНФ функції
Попарним порівнянням членів (кожного з членів з усіма подальшими) виявляємо склеюються пари членів:
перший і четвертий члени (результат склеювання);
другий і третій члени (результат склеювання);
другий і четвертий члени (результат склеювання);
третій і п'ятий члени (результат склеювання):
четвертий і п'ятий члени (результат склеювання).
Результати операції склеювання вводимо в вираз функції і проводимо операцію поглинання ними членів вихідного вираження: Член поглинає ті члени вихідного вираження, які містять, т. Е. Перший і четвертий. Ці члени викреслюються. Член поглинає другий і третій, а член x1? X3 - п'ятий член вихідного вираження.
Повторюємо операції склеювання і поглинання:
Член операції склеіваніяЗдесь склеюється лише пара членів і. (Склеювання пари членів і, призводить до того ж результату), результат склеювання х1. поглинає другий, третій, четвертий і п'ятий члени виразу.
Подальше проведення операцій склеювання і поглинання виявляється неможливим, скорочена форма вираження заданої функції (в даному прикладі вона збігається з мінімальною формою)
Члени скороченою форми (в розглянутому прикладі такими членами служать і х1 називаються простими импликантами функції.
Як бачимо, отримано вираз істотно простіше в порівнянні з СДНФ функції.
На рис. 3.27 приведена структурна схема логічного пристрою в базисі І, АБО, НЕ, побудована з використанням виразу (3.13).
^ Другий етап (отримання мінімальної форми).
Скорочена форма може містити зайві члени, виключення яких з виразу функції не вплине на значення функції.