Розпаралелювання уявлень багаторозрядних чисел НА модулярних СТРУКТУРАХ ДАНИХ
1 ГБОУ ВПО «Сургутський державний університет»
У роботі описується розпаралелювання уявлень надвеликих багаторозрядних чисел за допомогою системи залишкових класів (СОК), Китайської теореми про залишки (КТО) і Малої теореми Ферма. Таке уявлення багаторозрядних чисел дає переваги за часом для обчислювальних операцій при значному великому обсязі оброблюваних даних, так як вся обробка інформації проходить паралельно і незалежно один від одного. Паралельне представлення допускає відображення мільйон і більше розрядних чисел і може широко застосовуватися як в кодуванні інформації, в алгоритмах надшвидких обчислень, так і в тестуванні суперкомп'ютерів. Незважаючи на деякі недоліки, які в свою чергу можна подолати, модулярная система або система залишкових класів є унікальною математичної середовищем для паралельних обчислень. Тому таку систему можна враховуватися при розробці високопродуктивних систем на базі програмованих інтегральних логічних схем (ПЛІС) і багатоядерних процесорів.
китайська теорема про залишки
мала теорема Ферма
система залишкових класів
1. Амербаев В.М. Теоретичні основи машинної арифметики. - Алма-Ата: Наука, 1976. - 320 с.
2. Бухштаб А.А. Теорія чисел. - М. Наука, 1975.
3. Василенко О.М. Сучасні способи перевірки простоти чисел // Кібернетичний збірник. Нова серія. - 1988. - Вип. 25. - С. 162-187.
У сучасній алгоритмічної теорії великі і надвеликі числа грають важливу роль в криптографії для побудови шифрів різної складності і для тестування продуктивності суперкомп'ютерів [4, 8]. Дослідження надвеликих чисел [5] показало, що вони мають величини, які важко або майже неможливо поразрядно уявити в звичайних позиційних системах числення.
Якщо число A = 22147483647 звести в зазначену ступінь, то воно матиме більше мільйона розрядів. Тому такі числа недоцільно представляти в узагальненій позиційній системі числення в натуральному початковому стані.
Уявімо надвеликі багаторозрядні числа за допомогою звичайної позиційної системи числення, у вигляді інформаційної системи, показаної на схемою обчислення надвеликих чисел (рис. 1), і проаналізуємо їх.
На схемі показано, що на вхід алгоритму обчислення надвеликих чисел (стрілки зліва) надходять надвеликі багаторозрядні числа, стрілки «зверху-вниз» позначають позиційну систему числення і арифметичні операції. На виході алгоритму надвеликої число-результат. Однак якщо число-результат відобразити в звичайній позиційної системі, то виникають проблеми:
- Число не вміщається в типовій комп'ютерний діапазон [0. 231].
- Тимчасові витрати на подання числа в узагальненій позиційної системі.
- Навантаження на обсяг оперативної пам'яті, якщо число складається з пов'язаних списків.
За схемою абстрактного уявлення надвеликого многоразрядного числа (рис. 2) на виході виходить надвеликої число, яке не вміщається в типовій комп'ютерний діапазон. Наочно виконувати будь-які операції з таким числом неможливо, так як воно займає сотні сторінок файлів будь-якого типу з операційної системи Windows.
У зв'язку з цим надвеликі багаторозрядні числа A = 22147483648 ефективно представляти в непозиционной системі числення - системі залишкових класів, де немає переносів з молодших розрядів в старші.
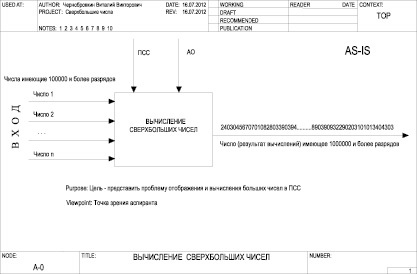
Мал. 1. Схема обчислення надвеликих чисел
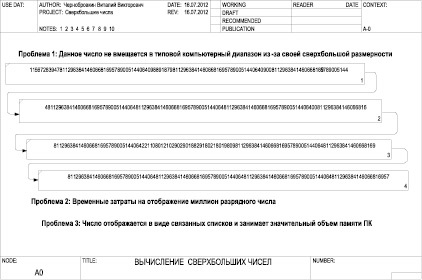
Мал. 2. Схема абстрактного уявлення надвеликого многоразрядного числа у вигляді пов'язаних списків
Існує проблема, яка полягає в наступному: якщо надвеликої багаторозрядні число представити за допомогою системи залишкових класів [5, 7], то число залишків, як і обрана система підстав, буде великим, що в свою чергу впливає на обчислювальні процеси.
Введемо числовий діапазон в двійковій позиційній системі [265537. 22147483648].
Затвердження 1 Число A = 22147483648, має кількість розрядів з діапазону [265537. 22147483648] і більш, можна називати надвеликих багаторозрядним числом.
Число, що має мільйон і більше розрядів, можна назвати надвеликих багаторозрядним, так як в реальному виконанні воно має велику чисельну значення.
Затвердження 2 Надвеликі багаторозрядні числа, представлені в системі залишкових класів, залежать від ваги позиційного рангу | Z | P [1], а значить, можуть складатися з великої безлічі вибраних модулів і відповідно залишків. Вага позиційного рангу | Z | P залежить від вмісту в ньому кількості простих чисел. При обчисленні надвеликих чисел в системі залишкових класів потрібно враховувати наступне рівність:
де A - число, результат обчислення; - підстави модулярной системи, взаємно прості числа.
Затвердження 3 надвеликої число можна представити за допомогою системи залишкових класів у вигляді залишків від відрахувань [3, 5, 6, 7]
a ≡ b (mod p). (2)
Можливість такого уявлення числа визначається наступними теоремами.
Теорема 1 (Китайська теорема про залишки) [2, 3, 5, 6, 7].
Будь-яке ціле позитивне число в системі залишкових класів можна представити у вигляді набору залишків (відрахувань) від ділення цього числа на обрані підстави (модулі) системи.
Доказ: Нехай число А = 22147483648 представлено в системі залишкових класів як
де a1, a2, ..., an - найменші невід'ємні залишків (відрахувань), утворені шляхом цілочисельного ділення числа A на обрані підстави
де pi - взаємно прості числа.
І якщо то уявлення числа (3) є єдиним за умови
Тоді число A буде виглядати наступним чином:
A ≡ a1 (mod p1);
A ≡ a2 (mod p2); (7)
A ≡ an (mod pn).
Теорема 2 Якщо числа в pi = p1, p2. pn попарно взаємно прості, то для будь-яких залишків a1, a2. an, таких, що 0 ≤ an ≤ pn при всіх i = 1, 2. n знайдеться число A, яке при діленні на pi дає залишок ai при всіх i = 1, 2. n
Доказ: Застосуємо індукцію по. При n = 1 твердження теореми очевидно. Нехай теорема справедлива при n = k - 1, тобто існує число M, що дає залишок ri при розподілі нa pi при i ∈. позначимо
d = a1, a2. ak-1. (8)
Розглянемо числа M, M + d, M + 2d. M (ak - 1) d. Покажемо, що хоча б одна з цих чисел дає залишок rk при розподілі на ak. Припустимо, що це не так. Оскільки кількість чисел одно ak, а можливих залишків при діленні цих чисел на ak може бути не більше ніж ak - 1 (тому що жодне число не дає залишок rk), то серед них знайдуться два числа, що мають рівні залишки. Нехай це числа
M + sdі M + tdM при 0 ≤ s ≤ ak
і 0 ≤ t ≤ ak і s ≠ t. (9)
Тоді їх різниця
(M + sd) - (M + td) = (s - t) d
ділиться на ak, що неможливо, тому що 0 <s – t Так як мова йде про мільйон розрядних числах, то опишемо реальні проблеми їх побудови в системі залишкових класів: Це означає, що, якщо ми будуємо надвеликі числа, у яких мільйон і більше розрядів, то кількість підстав системи буде залежати від розрядності цих чисел. Так, наприклад, якщо розрядність кожного з обраних підстав маленька, то відповідно кількість підстав потрібно збільшувати. І, навпаки, якщо розрядність обраних підстав велика, то їх потрібно зменшити до необхідної кількості. Тобто мова йде про розширення або звуження підстав системи залишкових класів [7]. Ще одна проблема полягає в тому, що при відображенні надвеликого числа A = 22147483648 в системі залишкових класів залишки можуть бути теж багаторозрядними. У загальному випадку вирішити перераховані вище проблеми можна за допомогою Малої теореми Ферма, доказ якої наведено в [2, 6] і Китайської теореми про залишки [2, 3, 5, 6, 7]. Основний сенс Малої теореми Ферма полягає в тому, що якщо p - позитивне просте число, a - ціле, тоді ap-1 ≡ 1 (mod p), якщо p - просте число, (10) значить, аk ≡ ar (mod p) і досить робити обчислення тільки для експонент, показник яких менше р - 1. Застосовуючи Китайську теорему про залишки, можна спростити відображення надвеликих чисел. Показавши їх у вигляді відрахувань ступенів по модулю n, якщо відомо його розкладання на прості множники. Припустимо, що кожен простий множник входить в цей розклад з кратністю 1, тому що саме в такому випадку метод найбільш ефективний. Припустимо, що розкладання має вигляд де 0 Для цілих чисел а і m спочатку знаходимо відрахування аm по кожному модулю pi. Якщо прості множники не надто великі, то обчислення будуть дуже швидкими навіть для великих m і a, оскільки нам допомагає це робити Мала теорема Ферма (п. 10). Припустимо, що обчислення зроблені, причому am ≡ r1 (mod p1) і 0 ≤ r1 ≤ p1; am ≡ r2 (mod p2) і 0 ≤ r2 ≤ p2; (12) am ≡ rk (mod pk) і 0 ≤ rk ≤ pk. Тому для визначення вирахування am по модулю n потрібно вирішити систему порівнянь: Нагадаємо, що модулі системи - різні попарно взаємно прості числа. Значить, по Китайської теоремі про залишки система завжди має рішення, наприклад r, 0 ≤ ri ≤ pi - 1. Більш того, будь-які два таких рішення порівнянні по модулю p1. pk = n .... Так як am теж рішення системи, маємо am ≡ r (mod n). Отже, r - відрахування amпо модулю n. Приклад. Сюр'ектівно відобразимо число A = 22147483648 у вигляді відрахувань за обраними підстав p1 = 11, p2 = 13, p3 = 17, p4 = 19. Змінивши при цьому ступінь зазначеного числа на одиницю 2147483648 - 1 = 2147483647, застосуємо Малу теорему Ферма, для чого знайдемо залишки від ділення ступеня 2147483647 (на p1) кожного обраного підстави p1, p2, p3, p4. тоді pi-1 = 11 - 1 = 10; pi-2 = 13 - 1 = 12; pi-3 = 17 - 1 = 16; pi-4 = 19 - 1 = 18; (14) a'1 = 2147483647 mod 10 = 7; a'2 = 2147483647 mod 12 = 7; (15) a'3 = 2147483647 mod 16 = 15; a'4 = 2147483647 mod 18 = 1. a1 = 22147483647 ≡ 27 (mod 11); a2 = 22147483647 ≡ 27 (mod 13); (16) a3 = 22147483647 ≡ 215 (mod 17); a4 = 22147483647 ≡ 21 (mod 19). Остаточно число A = 22147483647 буде виглядати: 27 ≡ 7 (mod 11); 27 ≡ 11 (mod 13); (17) 215 ≡ 9 (mod 17); 2 ≡ 2 (mod 19). 1. Розпаралелювання уявлень надвеликих багаторозрядних чисел за допомогою системи залишкових класів дає перевагу за часом для обчислень при великому обсязі оброблюваних даних, так як вся обробка інформації відбувається паралельно і незалежно один від одного. 2. Будь-яке багаторозрядні число можна представити у вигляді залишків від статечних відрахувань. 3. Над представленими паралельним чином числами можна проводити прискорені паралельні обчислення. 4. Якщо утворення залишків ai, проводиться незалежно один від одного, то кожне обчислення буде також відбуватися незалежно один від одного. Інютін С.А. д.т.н. професор кафедри «Проектування обчислювальних комплексів», ФГБОУ ВПО «Російський державний технологічний університет ім. К.Е. Ціолковського (МАТИ) », м.Москва; Бахарєв М.С. д.т.н. професор кафедри «Нафтогазова справа», ФГБОУ ВПО «Сургутський інститут нафти і газу, філія Тюменського державного нафтогазового університету», м Сургут; Криштоп В.В. д.ф.-м.н. професор, завідувач кафедри «Фізика», Далекосхідний державний університет шляхів сполучення, м Хабаровськ, професор Університету Kwangwoon University, Korea. Пропонуємо вашій увазі журнали, що видаються у видавництві «Академія природознавства» (Високий імпакт-фактор РИНЦ, тематика журналів охоплює всі наукові напрямки) Науковий журнал | ISSN 1812-7339 | ПІ №77-63397 Служба технічної підтримки - [email protected] Відповідальний секретар журналу Бізенкова М.Н. - [email protected]
Матеріали журналу доступні на умовах ліцензії Creative Commons «Attribution» ( «Атрибуція») 4.0 Всесвітня.Схожі статті