Пряма в просторі може бути задана як лінія перетину двох площин. Так як точка прямої належить кожній з площин, то її координати повинні задовольняти рівнянням обох площин, тобто задовольняти системі з двох рівнянь.
Отже, якщо рівняння двох непаралельних площин:
то пряма, що є їх лінією перетину, задається системою рівнянь:
І навпаки, точки, що задовольняють такій системі рівнянь, утворюють пряму, яка є лінією перетину площин, чиї рівняння утворюють цю систему.
Рівняння (1.1) називаютобщімі рівняннями прямої в просторі.
Зауваження 1.1. Будь-які спроби за допомогою перетворень рівнянь системи (1.1) отримати одне (лінійне) рівняння, що задає пряму, приречені на невдачу. Одне рівняння - це рівняння площині.
Загальні рівняння прямої «незручні» для отримання інформації про стан прямої.
Наприклад, щоб знайти координати якої-небудь точки на прямій, потрібно провести досить складні обчислення. А саме, задати довільно якусь координату, підставити її в систему (1.1) і з отриманої системи двох рівнянь з двома невідомими знайти дві інші координати. Причому може виявитися, що отримана система не має рішень. Тоді потрібно довільно задати іншу координату і з системи знайти дві що залишилися координати.
Приклад 1.1. Потрібно знайти якусь точкуна прямий
Рішення. Покладемо. отримаємо систему
Вирішуючи її, знаходимо,.
Можна задати пряму в просторі і в інший спосіб.
Ненульовий вектор, що лежить на прямій (паралельний їй) називається напрямних вектором прямої.
Нехай для прямої відомі її спрямовує вектор точка, що лежить на цій прямій. Пусть- довільна (поточна) точка прямої. Позначимо черезірадіус-вектори точекісоответственно (рисунок 1.1).
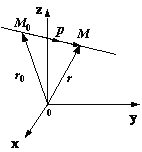
Малюнок 1.1 - Векторне рівняння прямої
Тоді вектор коллінеарен векторуі, отже ,, де-деяке число. З малюнка 1.1 видно, що
Це рівняння називаетсявекторним рівнянням прямої іліуравненіем в векторній формі. При кожному значенні параметрами будемо отримувати нову точкуна прямий.
Зауваження 1.2. Якщо в якості параметравзять час, то точкабудет рухатися по прямій з швидкістю, причому в момент врементее положення збігається з точкою. Вектор швидкості точки збігається з вектором.
Від векторного співвідношення (1.2) перейдемо до співвідношень координат. Так якось координати точки, то ,,. З формули (1.2) отримаємо
Отримана система рівнянь називаетсяпараметріческімі рівняннями прямої.
Звернемо увагу на те, що по параметричних рівнянь легко встановити направляючий вектор прямої і координати однієї з її точок. Коефіцієнти перед параметром дають координати направляючого вектора, а вільні члени в правій частині - координати точки на прямій.
Так як направляючий вектор прямої визначається з точністю до множення на число, відмінне від нуля, а в якості точки можна взяти будь-яку точку прямої, то одна і та ж пряма може здаватися нескінченним безліччю систем параметричних рівнянь. Причому різні системи можуть бути не схожими один на одного.
З рівнянь (1.3) висловимо параметр:
,,.
Так як у всіх трьох співвідношеннях параметр має одне і те ж значення, то
Ці рівняння називаютсяканоніческімі рівняннями прямої.
Зауваження 1.3. У канонічних рівняннях прямої допускається в знаменнику писати 0. Це не означає, що можна виконати поділ на 0. Просто з канонічних рівнянь ми отримуємо інформацію про те, що спрямовує вектор прямої має координати, з яких одна нульова.
Приклад 1.2. Пряма з канонічними рівняннями:
має направляючий вектор.
Зауваження 1.4. Канонічні рівняння прямої (1.5) не можна розглядати як одне рівняння (в них два знака «=» і отже, два рівняння). Вони складають своєрідний спосіб записану систему з двох рівнянь:
Можливі, втім, ще два записи системи.