Визначимо проекції швидкості (1.1) точки в момент часу t1 = 2 c:
Величина швидкості 16,3 м / с.
Нормальне прискорення точки. Тоді радіус кривизни траєкторії. Визначимо. З рис. 1.1 слід
де a - кут між повним прискоренням і нормальним прискоренням. За умовою - прискорення вільного падіння. Також з малюнка отримуємо, що. Отже, радіус кривизни траєкторії. Обчислимо.
Приклад 2. Матеріальна точка рухається відповідно до рівняннями:
x = A + Bt + Ct 3. y = Kt + Lt 2, (1.2)
де А = 3 м, В = 1 м / с, С = -1 м / с 3. K = 1,5 м / с, L = 2 м / с 2.
Знайти координати, швидкість і ускореніеточкі в момент часу t = 1 c.
Рішення. Координати точкінайдем, підставивши в рівняння руху (1.2) числові значення коефіцієнтів А, В, С, K, L ічасу t:
Проекції миттєвої швидкості точки на осі х, y є перші похідні від координат (1.2) за часом:
При t = 1 c; . Величина швидкості м / с.
Проекції прискорення точки знайдемо, взявши перші похідні від проекцій швидкості (1.3) за часом:
Величина прискорення точки.
При t = 1 c м / с 2. м / с 2. м / с 2.
Приклад 3. Тіло обертається навколо нерухомої осі за законом
де А = 10 радий, В = 20 рад / с, С = -2 рад / с 2. Знайти швидкість і прискорення точки, знаходячи-щейся на відстані r = 0,1 м від осі обертання, для моменту часу t = 4 с . Показати вектори швидкості і прискорення на малюнку.
Рішення. Швидкість точки тіла, що обертається навколо нерухомої осі, визначається за формулою. де w - модуль кутової швидкості тіла. Кутову швидкість w знайдемо, взявши першу виробниц-ву від кута повороту (1.5) за часом:
У момент часу t = 4 c модуль кутової швидкості
Швидкість точки м / с.
Повний прискорення точки, що рухається по кривій лінії, може бути знайдено як геометрична сума тангенціального прискорення. спрямованого по дотичній до траєкторії, і нормального прискорення. спрямованого до центру кривизни траєкторії (рис. 1.2):
Так як вектори взаємно перпендикулярні, то модуль прискорення. (1.7)
Модулі тангенціального і нормального прискорення точки тіла, що обертається виражаються формулами:
де e - модуль його кутового прискорення.
Підставляючи вирази аt і аn в формулу (1.7), знаходимо
Кутове прискорення знайдемо, взявши першу виробниц-ву від кутової швидкості (1.6) за часом:
Підставляючи значення w, e і r в формулу (1.9), отримуємо
Вектор дотичного прискорення спрямований проти швидкості, тому що кутове прискорення.
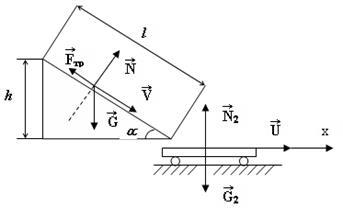
Приклад 4. Ящик масою m1 = 20 кг зісковзує по лотку довжиною l = 2 м з коефіцієнтом тертя f = 0,1 на нерухому візок з піском і застряє в ньому. Візок з піском масою m2 = 80 кг може вільно (без тертя) переме-тися по рейках в горизонтальному напрямку. Опрі-ділити швидкість u візки з ящиком, якщо лоток Накло-нен під кутом a = 30 ° до рейок.
Рішення. Візок і ящик можна розглядати як систему двох непружно взаємодіючих тіл. Але ця система не замкнута, так як на неї діють зовнішні сили: сили тяжіння G1 = m1 g і G2 = m2 g і сила реакції N2 (рис. 1.3). Тому застосувати закон збереження імпульсу в загальному до системи "ящик - візок" не можна. Однак, так як проекції зазначених сил на напрям осі х, що збігається з напрямком рейок, дорівнюють нулю, то проекцію імпульсу системи на цей напрям можна вважати постійної, тобто
де p1x і p2x - проекції імпульсу ящика і візки з піском в момент падіння ящика на візок; p'1x і p'2x - ті ж величини після падіння ящика.
Розглядаючи тіла системи як матеріальні точки, висловимо в рівність (1.10) імпульси тел через їх маси і швидкості, з огляду на, що р2x = 0 (візок до взаємодій-наслідком з ящиком лежала), а також що після взаємо-дії обидва тіла системи рухаються з однією і тією ж швидкістю і:
де v1 - модуль швидкості ящика перед падінням на візок; - проекція цієї швидкості на вісь х.
З (1.11) випливає. (1.12)
Модуль швидкості v1 визначимо із закону збереження енергії при русі ящика по лотку з урахуванням сили тертя Fтр:
Підставивши вираз v1 в формулу (1.12), отримаємо
Обчислюємо швидкість візки:
Приклад 5. Пором масою m1 і довжиною l стоїть на нерухомій воді. На його кормі знаходиться контейнер масою m2. Потім контейнер був переміщений на носову частину порома за допомогою власного крана. На яку відстань s переміститься паром щодо дна? Силами тертя і опору пре-знехтувати.
Рішення. Система паром-контейнер щодо горизонтального напрямку може розглядатися як замкнута. Із закону збереження імпульсу випливає, що внутрішні сили замкнутої системи тіл не можуть змінити положення центру мас системи. Отже, при переміщенні контейнера центр мас системи т. З не змінить свого положення щодо дна. Координата центру мас xc системи визначається виразом, де m - маса системи; mi - маси тіл.
Виберемо початок системи координат так, щоб вісь Oy проходила в початковий момент через точку C1 - центр мас порома. Позначимо координати x1 центру мас порома т. C1 і x2 - центру мас контейнера т. C2 - до переміщення (рис. 1.4), x'1. x'2 - після переміщення.
Положення центру мас системи не змінилося, отже
З малюнка слід, що. - до переміщення,. - після переміщення. Отримуємо з (1.14):
Приклад 6. При пострілі з пружинного пістолета вертикально вгору куля масою m = 20 г піднялася на висоту h = 5 м. Визначити жорсткість k пружини пістолета, якщо вона була стиснута на х = 10 см. Масою пружини і силами тертя знехтувати.
Рішення. Розглянемо систему пружина - куля. Так як на тіла системи діють тільки консервативні сили, то для вирішення завдання можна застосувати за-кон збереження енергії в механіці. Згідно з ним, повна механічна енергія Е1 системи в початковому стані (в даному випадку перед пострілом) дорівнює повній енер-гии Е2 в кінцевому стані (коли куля піднялася на висоту h), т. Е.
де Т1. Т2. П1 і П2 - кінетичні і потенційні енергії системи в початковому і кінцевому станах. Так як кінетичні енергії кулі в початковому і ко-нечном станах дорівнюють нулю, то рівність (1.15) при-мет вид
Приймемо потенційну енергію кулі в полі сил тяго-тенія Землі, коли куля покоїться на стислій пружині, що дорівнює нулю, а висоту підйому кулі будемо відраховувати від торця стислої пружини. Тоді енергія системи в на-початковому стані буде дорівнює потенційної енергії стислої пружини, тобто . а в кінцевому перебуваючи-ванні - потенційної енергії кулі на висоті h. тобто .
Підставивши вирази П1 і П2 в формулу (2), най-дем. звідки. (1.17) Перевіримо, чи дає отримана формула одиницю жорсткості k. Для цього в праву частину формули (1.17) замість величин підставимо їх одиниці вимірювання:
Переконавшись, що отримана одиниця є оди-ницей жорсткості (1 Н / м), підставимо в формулу (3) зна-чення величин і зробимо обчислення:
Приклад 7. Куля масою m1. рухомий горизон-тально з деякою швидкістю v1, зіткнувся з нерухомим шаром масою т2. Кулі абсолютно пружні, удар прямий, центральний. Яку частку k своєї кінетичної енергії першу кулю передав другому?
Рішення. Частка енергії, переданої першим шаром другого, виразиться співвідношенням
де - кінетична енергія і швидкість першої кулі до удару; u2 і T2 - швидкість і кінетична енергія другої кулі після удару.
Як видно з формули (1.18), для визначення k треба знайти. Згідно з умовою задачі, імпульс системи двох куль щодо горизонтального напрямку не змінюється і механічна енергія куль в інші види не переходить. Користуючись цим, знайдемо:
Вирішимо спільно рівняння (1.19) і (1.20):
Підставивши вираз u2 (1.21) в формулу (1.18) і скоротивши на v1 і m1. отримаємо
З знайденого співвідношення видно, що частка переданий-ної енергії залежить тільки від мас зіштовхуються куль.